Definição de aceleração centrípeta, fórmulas, cálculos, exercícios

O aceleração centrípeta para_c, Também chamada de radial ou normal, é a aceleração que um objeto em movimento carrega quando descreve um caminho circular. Sua magnitude é v^dois/ r, Onde r é o raio do círculo, é direcionado para o centro dele e é responsável por manter o móbile em seu caminho.

As dimensões da aceleração centrípeta são comprimento por unidade de tempo ao quadrado. No Sistema Internacional são m / s^dois. Se por algum motivo a aceleração centrípeta desaparecer, também desaparecerá a força que força o móvel a manter o caminho circular.

É o que acontece com um carro que tenta fazer a curva em uma pista plana e gelada, onde o atrito entre o solo e as rodas é insuficiente para o carro fazer a curva. Portanto, a única possibilidade que resta é se mover em linha reta e é por isso que sai da curva.

Índice do artigo

• 1 movimentos circulares
• 2 A força centrípeta
• 3 Fórmulas para aceleração centrípeta
• 4 Exercício resolvido
  • 4.1 Resposta
• 5 referências

Movimentos circulares

Quando um objeto se move em um círculo, em todos os momentos a aceleração centrípeta é dirigida radialmente em direção ao centro da circunferência, uma direção que é perpendicular ao caminho seguido.

Como a velocidade é sempre tangente ao caminho, a velocidade e a aceleração centrípeta tornam-se perpendiculares. Portanto, velocidade e aceleração nem sempre têm a mesma direção.

Nessas circunstâncias, o móbile tem a possibilidade de descrever a circunferência com velocidade constante ou variável. O primeiro caso é conhecido como Movimento Circular Uniforme ou MCU por sua sigla, o segundo caso será um Movimento Circular Variável.

Em ambos os casos, a aceleração centrípeta é responsável por manter o móvel girando, garantindo que a velocidade varie apenas na direção e na direção.

Porém, para se ter um Movimento Circular Variável, seria necessário outro componente da aceleração no mesmo sentido da velocidade, que se encarrega de aumentar ou diminuir a velocidade. Este componente de aceleração é conhecido como aceleração tangencial.

O movimento circular variável e o movimento curvilíneo em geral têm ambos os componentes de aceleração, porque o movimento curvilíneo pode ser imaginado como o caminho através de inúmeros arcos circunferenciais que constituem o caminho curvo..

A força centrípeta

Agora, uma força é responsável por fornecer a aceleração. Para um satélite orbitando a Terra, é a força da gravidade. E como a gravidade sempre atua perpendicularmente à trajetória, ela não altera a velocidade do satélite..

Nesse caso, a gravidade atua como um força centrípeta, que não é uma classe especial ou separada de força, mas uma que, no caso do satélite, é dirigida radialmente em direção ao centro da terra.

Em outros tipos de movimento circular, por exemplo, um carro fazendo uma curva, o papel da força centrípeta é desempenhado pelo atrito estático e para uma pedra amarrada a uma corda que gira em círculos, a tensão na corda é a força que força o celular para girar.

Fórmulas para aceleração centrípeta

A aceleração centrípeta é calculada pela expressão:

ac = v^dois/ r

Esta expressão será derivada abaixo. Por definição, a aceleração é a mudança na velocidade ao longo do tempo:

O celular leva um tempo Δt no percurso, que é pequeno, pois os pontos são muito próximos.

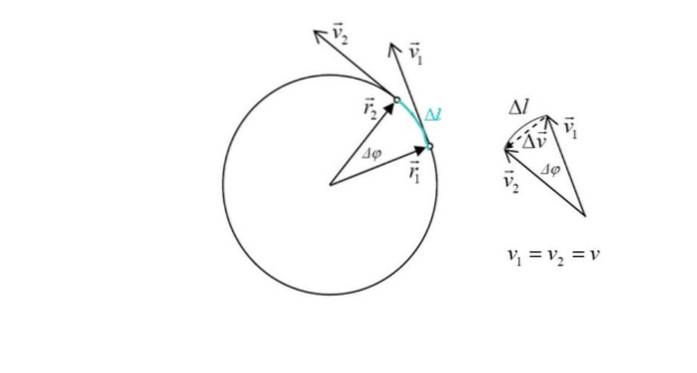
A figura também mostra dois vetores de posição r₁ Y r_dois, cujo módulo é o mesmo: o raio r da circunferência. O ângulo entre os dois pontos é Δφ. Em verde destaca o arco atravessado pelo celular, denotado como Δl.

Na figura à direita pode-se ver que a magnitude de Δv, a mudança na velocidade é aproximadamente proporcional a Δl, uma vez que o ângulo Δφ é pequeno. Mas a mudança na velocidade está precisamente relacionada à aceleração. Do triângulo pode-se ver, adicionando os vetores que:

v₁ + Δv = v_dois → Δv = v_dois - v₁

Δv é interessante, pois é proporcional à aceleração centrípeta. Pela figura pode-se ver que como o ângulo Δφ é pequeno, o vetor Δv é essencialmente perpendicular a ambos v₁ Como a v_dois e aponta para o centro da circunferência.

Embora até agora os vetores estejam destacados em negrito, para os efeitos de natureza geométrica que se seguem, trabalhamos com os módulos ou magnitudes desses vetores, dispensando a notação vetorial.

Outra coisa: você precisa fazer uso da definição de ângulo central, que é:

Δφ= Δl / r

Agora as duas figuras são comparadas, que são proporcionais, pois o ângulo Δφ é comum:

Dividindo por Δt:

para_c= v^dois/ r

Exercício resolvido

Uma partícula se move em um círculo de raio de 2,70 m. Em um determinado momento sua aceleração é de 1,05 m / s^dois em uma direção que forma um ângulo de 32,0º com a direção do movimento. Calcule sua velocidade:

a) Naquela época

b) 2,00 segundos depois, assumindo aceleração tangencial constante.

Responder

É um movimento circular variado, pois o enunciado indica que a aceleração tem um determinado ângulo com a direção do movimento que não é 0º (não poderia ser um movimento circular) nem 90º (seria um movimento circular uniforme).

Portanto, os dois componentes -radial e tangencial- coexistem. Eles serão denotados como um_c já_t e são desenhados na figura a seguir. O vetor em verde é o vetor líquido de aceleração ou simplesmente aceleração para.

a) Cálculo dos componentes de aceleração

para_c = a.cos θ = 1,05 m / s^dois . cos 32,0º = 0,89 m / s^dois (em vermelho)

para_t = a.sen θ = 1,05 m / s^dois . sen 32,0º = 0,57 m / s^dois (em laranja)

Cálculo da velocidade do celular

Desde uma_c = v^dois/ r, então:

v = v_ou +para_t. t = 1,6 m / s + (0,57 x 2) m / s = 2,74 m / s

Referências

1. Giancoli, D. Physics. 2006. Princípios com aplicativos. Sexta edição. Prentice Hall. 107-108.
2. Hewitt, Paul. 2012. Ciência Física Conceitual. Quinta edição.Pearson. 106 - 108.