O aceleração instantânea É a mudança que a velocidade experimenta por unidade de tempo a cada instante do movimento. No exato momento em que o “dragster”Da imagem que foi fotografada, ela suportou uma aceleração de 29,4 m / sdois. Isso significa que, naquele momento, sua velocidade estava sendo aumentada em 29,4 m / s no intervalo de 1 s. Isso é equivalente a 105 km / h em apenas 1 segundo.
Uma competição de dragster é facilmente modelada assumindo que o carro de corrida é um objeto pontual. P que se move em linha reta. Nesta linha é escolhido um eixo orientado com a origem OU que chamaremos de eixoBOI) ou apenas eixo x.
As variáveis cinemáticas que definem e descrevem o movimento são:
Todos eles são quantidades vetoriais. Portanto, eles têm uma magnitude, uma direção e um sentido.
No caso de movimento retilíneo, existem apenas duas direções possíveis: positivo (+) na direção de (BOI) ou negativo (-) na direção oposta de (BOI) Portanto, é possível dispensar a notação vetorial formal e usar os sinais para indicar o sentido da magnitude..
Índice do artigo
Suponha que no instante t a partícula tem velocidade v (t) e no instante t ' sua velocidade é v (t ').
Então, a mudança que a velocidade teve naquele período de tempo foi Δv = v (t ') - v (t). Daí a aceleração no lapso de tempo Δt = t '- t , seria dado pelo quociente:
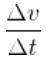
Este quociente é a aceleração média emm no período de tempo Δt entre os instantes t e t '.
Se quiséssemos calcular a aceleração apenas no tempo t, então t 'deveria ser uma quantidade insignificantemente maior do que t. Com este Δt, que é a diferença entre os dois, deve ser quase zero.
Matematicamente é indicado da seguinte forma: Δt → 0 e é obtido:
EU) Uma partícula se move ao longo do eixo X com velocidade constante v0 = 3 m / s. Qual será a aceleração da partícula?
A derivada de uma constante é zero, portanto a aceleração de uma partícula se movendo com velocidade constante é zero.
II) Uma partícula se move no eixo x e sua velocidade muda com o tempo de acordo com a seguinte fórmula:
v (t) = 2 - 3t
Onde a velocidade é medida em m / se o tempo em s. Qual será a aceleração da partícula?
)
O resultado é interpretado assim: para qualquer instante a aceleração é -3 m / s.
Entre os instantes 0 se 2/3 s a velocidade é positiva enquanto a aceleração é negativa, ou seja, nesse intervalo a partícula diminui sua velocidade ou desacelera.
No instante 2/3 s, sua velocidade torna-se zero, mas como permanece uma aceleração de -3 m / s, a partir desse instante a velocidade se inverte (torna-se negativa).
Nos instantes após ⅔ s, a partícula acelera, pois cada vez que sua velocidade se torna mais negativa, ou seja, sua velocidade (módulo de velocidade) aumenta.
III) A figura mostra uma curva que representa a velocidade em função do tempo, para uma partícula que se move ao longo do eixo X. Encontre o sinal da aceleração nos tempos t1, tdois e você3. Indique também se a partícula está acelerando ou desacelerando.
A aceleração é a derivada da função velocidade, portanto é equivalente à inclinação da reta tangente à curva v (t) para um dado instante t.
Por um instante t1, a inclinação é negativa, então a aceleração é negativa. E como nesse instante a velocidade é positiva, podemos afirmar que nesse instante a partícula está desacelerando.
Por um instante tdois a linha tangente à curva v (t) é horizontal, então sua inclinação é zero. O celular tem aceleração zero, portanto em tdois a partícula não acelera nem desacelera.
Por um instante t3, a inclinação da reta tangente à curva v (t) é positiva. Com uma aceleração positiva a partícula está realmente acelerando, porque naquele momento a velocidade também é positiva.
Na seção anterior, a aceleração instantânea foi definida a partir da velocidade instantânea. Ou seja, se a velocidade é conhecida a cada instante, então também é possível saber a aceleração a cada instante do movimento..
O processo reverso é possível. Ou seja, sabendo a aceleração para cada instante, então a velocidade instantânea pode ser calculada.
Se a operação que permite ir da velocidade à aceleração é a derivada, a operação matemática oposta é a integração.
A aceleração de uma partícula se movendo ao longo do eixo X é a (t) = ¼ tdois. Onde t é medido em segundos e a em m / s. Determine a aceleração e velocidade da partícula a 2 s de movimento, sabendo que no instante inicial t0 = 0 estava em repouso.
Aos 2 s, a aceleração é de 1 m / sdois e a velocidade para o instante t será dada por:
Um objeto se move ao longo do eixo X com uma velocidade em m / s, dada por:
v (t) = 3 tdois - 2 t, onde t é medido em segundos. Determine a aceleração às vezes: 0s, 1s, 3s.
Tomando a derivada de v (t) em relação a t, a aceleração em qualquer instante é obtida:
a (t) = 6t -2
Então a (0) = -2 m / sdois ; a (1) = 4 m / sdois ; a (3) = 16 m / sdois .
Uma esfera de metal é liberada do topo de um edifício. A aceleração de queda é a aceleração da gravidade que pode ser aproximada pelo valor 10 m / s2 e apontando para baixo. Determine a velocidade da esfera 3 s após ela ter sido liberada.
Este problema envolve a aceleração da gravidade. Tomando a direção vertical como positiva para baixo, temos que a aceleração da esfera é:
a (t) = 10 m / sdois
E a velocidade será dada por:
Uma esfera de metal é atirada para cima com uma velocidade inicial de 30 m / s. A aceleração do movimento é a aceleração da gravidade que pode ser aproximada pelo valor de 10 m / sdois e apontando para baixo. Determine a velocidade da esfera 2 se 4 s após ter sido disparada.
A direção vertical será considerada positiva até em cima. ENesse caso, a aceleração do movimento será dada por
a (t) = -10 m / sdois
A velocidade em função do tempo será dada por:
Após 4 s do disparo, a velocidade será 30 - 10 ∙ 4 = -10 m / s. O que significa que em 4 s a esfera desce com uma velocidade de 10 m / s.
Ainda sem comentários