
Medida de arco (geometria), tipos de arcos, exemplos
O arco, na geometria, é qualquer linha curva que conecta dois pontos. Uma linha curva, ao contrário de uma linha reta, é aquela cuja direção é diferente em cada ponto dela. O oposto de um arco é um segmento, pois esta é uma seção reta que une dois pontos.
O arco mais freqüentemente usado em geometria é o arco de circunferência. Outros arcos de uso comum são o arco parabólico, o arco elíptico e o arco catenário. A forma do arco também é freqüentemente usada na arquitetura como um elemento decorativo e um elemento estrutural. É o caso das vergas das portas e janelas, bem como das pontes e aquedutos..

Índice do artigo
- 1 O arco e sua medida
- 2 tipos de arcos
- 2.1 Arco circular
- 2.2 Arco parabólico
- 2.3 Arco catenário
- 2.4 Arco elíptico
- 3 exemplos de arcos
- 3.1 Exemplo 1
- 3.2 Exemplo 2
- 4 referências
O arco e sua medida
A medida de um arco é seu comprimento, que depende do tipo de curva que conecta os dois pontos e de sua localização..
O comprimento de um arco circular é um dos mais simples de calcular, porque o comprimento do arco completo ou perímetro de uma circunferência é conhecido.
O perímetro de um círculo é dois pi vezes seu rádio: p = 2 π R. Sabendo disso, se você quiser calcular o comprimento s de um arco circular de ângulo α (medido em radianos) e raio R, uma proporção é aplicada:
(s / p) = (α / 2 π)
Então, limpar s da expressão anterior e substituindo o perímetro p por sua expressão em função do raio R, se tem:
s = (α / 2 π) p = (α / 2 π) (2 π R) = α R.
Ou seja, a medida de um arco circular é o produto de sua abertura angular vezes o raio do arco circular.
Para um arco em geral, o problema é mais complicado, a ponto de os grandes pensadores da antiguidade afirmarem que era uma tarefa impossível..
Não foi até o advento do cálculo diferencial e integral em 1665, que o problema da medição de qualquer arco foi resolvido satisfatoriamente.
Antes da invenção do cálculo diferencial, as soluções só podiam ser encontradas usando linhas poligonais ou arcos de circunferência que se aproximavam do arco verdadeiro, mas essas soluções não eram exatas..
Tipos de arcos
Do ponto de vista da geometria, os arcos são classificados de acordo com a linha curva que une dois pontos no plano. Existem outras classificações de acordo com seu uso e forma arquitetônica.
Arco circular
Quando a linha que conecta dois pontos do plano é um pedaço da circunferência de um determinado raio, temos um arco circular. A Figura 2 mostra um arco circular c de raio R conectando os pontos A e B.
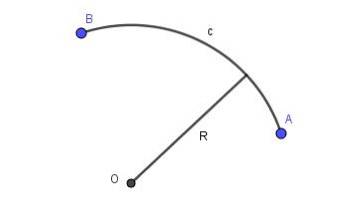
Arco parabólico
A parábola é o caminho percorrido por um objeto que foi lançado obliquamente no ar. Quando a curva que une dois pontos é uma parábola, então temos um arco parabólico como o mostrado na figura 3.
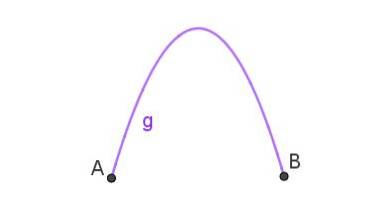
Esta é a forma do jato de água que sai de uma mangueira apontando para cima. O arco parabólico pode ser observado nos mananciais..

Arco catenário
O arco catenário é outro arco natural. A catenária é a curva que se forma naturalmente quando uma corrente ou corda fica solta em dois pontos separados.
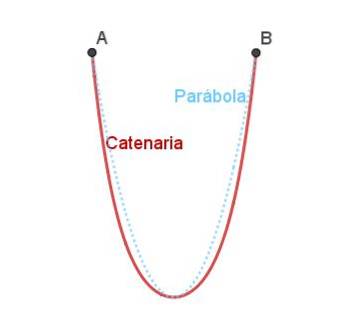
A catenária é semelhante à parábola, mas não é exatamente a mesma que pode ser vista na figura 4.
O arco catenário invertido é usado na arquitetura como um elemento estrutural de alta resistência à compressão. Na verdade, pode ser demonstrado que é o tipo de arco mais forte de todas as formas possíveis..
Para construir um arco catenário sólido, basta copiar a forma de uma corda ou corrente pendurada e, em seguida, a forma copiada é virada para reproduzi-la no dintel da porta ou janela.
Arco elíptico
Um arco é elíptico se a curva que conecta dois pontos for uma parte ou seção de uma elipse. A elipse é definida como o lugar geométrico dos pontos cuja distância a dois pontos dados sempre somam uma quantidade constante.
A elipse é uma curva que aparece na natureza: é a curva da trajetória dos planetas ao redor do Sol, conforme demonstrado por Johannes Kepler no ano de 1609.
Na prática, uma elipse pode ser desenhada fixando-se duas escoras no chão ou dois alfinetes no papel e amarrando-se um barbante a eles. A corda é então tensionada com o marcador ou lápis e a curva é traçada. Um pedaço de elipse é um arco elíptico. A animação a seguir ilustra como a elipse é desenhada:
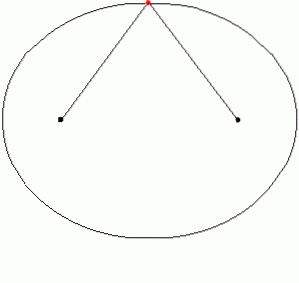
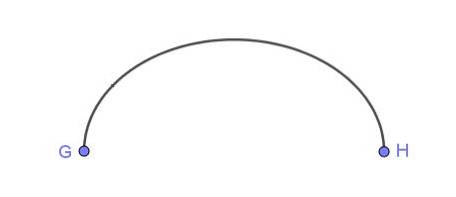
A Figura 6 mostra um arco elíptico conectando os pontos G e H.
Exemplos de arcos
Os exemplos a seguir referem-se a como calcular o perímetro de alguns arcos específicos.
Exemplo 1
A Figura 7 mostra uma janela com acabamento em arco circular cortado. As dimensões mostradas na figura estão em pés. Calcule o comprimento do arco.
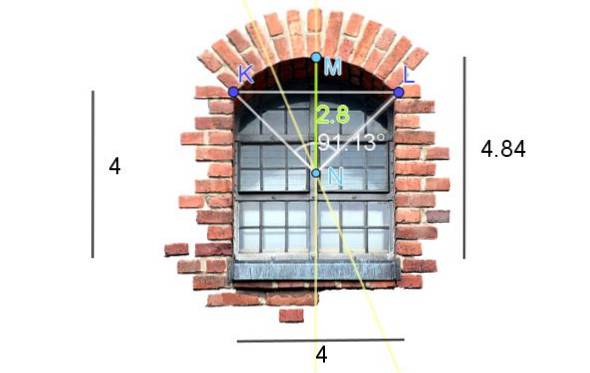
Para obter o centro e o raio do arco circular do lintel da janela, as seguintes construções são feitas na imagem:
-O segmento KL é desenhado e sua bissetriz é desenhada.
-Em seguida, localiza-se o ponto mais alto do lintel, que chamamos de M. Em seguida, considera-se o segmento KM e traça-se sua mediatriz..
A interceptação das duas bissetoras é o ponto N e também é o centro do arco circular.
-Agora devemos medir o comprimento do segmento NM, que coincide com o raio R do arco circular: R = 2,8 pés.
-Para saber o comprimento do arco além do raio, é necessário saber o ângulo que o arco forma. Que pode ser determinado por dois métodos, ou é medido com um transferidor ou, alternativamente, é calculado usando trigonometria.
No caso mostrado, o ângulo formado pelo arco é 91,13º, que deve ser convertido para radianos:
91,13º = 91,13º * π / 180º = 1,59 radianos
Finalmente calculamos o comprimento s do arco usando a fórmula s = α R.
s = 1,59 * 2,8 pés = 4,45 pés
Exemplo 2
Encontre o comprimento do arco elíptico mostrado na figura 8, conhecendo o semi-eixo maior r e o semi-eixo menor s da elipse.
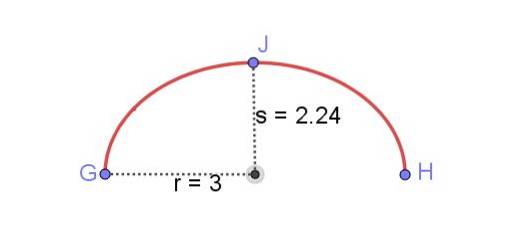
Encontrar o comprimento de uma elipse foi um dos problemas mais difíceis da matemática por muito tempo. Você pode obter soluções expressas por integrais elípticas, mas para ter um valor numérico, você precisa expandir essas integrais em séries de potências. Um resultado exato exigiria termos infinitos dessas séries.
Felizmente, o gênio matemático hindu Ramanujan, que viveu entre 1887 e 1920, encontrou uma fórmula que se aproxima com muita precisão do perímetro de uma elipse:
Perímetro de uma elipse = π [3 (r + s) - √ ((3r + s) (r + 3s))]
O perímetro de uma elipse com r = 3 cm es = 2,24 cm é 16,55 cm. No entanto, o arco elíptico mostrado tem metade desse valor:
Comprimento do arco elíptico GH = 8,28 cm.
Referências
- Clemens S. 2008. Geometria e Trigonometria. Pearson Education.
- García F. Procedimentos numéricos em Java. Comprimento de uma elipse. Recuperado de: sc.ehu.es
- Geometria dinâmica. Arcos. Recuperado de geometriadinamica.es
- Piziadas. Elipses e parábolas ao nosso redor. Recuperado de: piziadas.com
- Wikipedia. Arco (geometria). Recuperado de: es.wikipedia.com


Ainda sem comentários