
Carga axial como é calculada e exercícios resolvidos
O carga axial É a força que se dirige paralelamente ao eixo de simetria de um elemento que compõe uma estrutura. A força axial ou carga pode ser tensão ou compressão. Se a linha de ação da força axial coincidir com o eixo de simetria que passa pelo centroide do elemento considerado, então se diz que é uma carga ou força axial concêntrica.
Ao contrário, se é uma força axial ou carga paralela ao eixo de simetria, mas cuja linha de ação não está no próprio eixo, é uma força axial excêntrica.
-
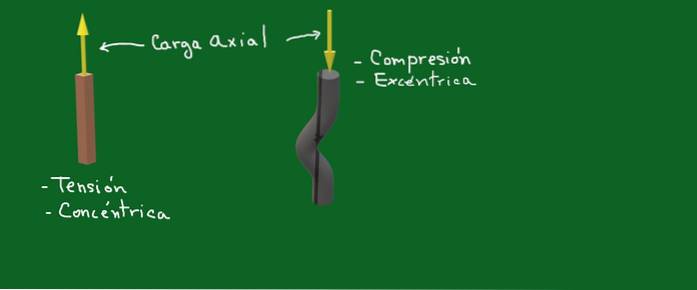
Figura 1. Carga axial. Fonte: self made
Na figura 1, as setas amarelas representam forças ou cargas axiais. Em um caso é uma força de tensão concêntrica e no outro estamos lidando com uma força de compressão excêntrica.
A unidade de medida para carga axial no sistema internacional SI é o Newton (N). Mas outras unidades de força, como quilograma-força (kg-f) e libra-força (lb-f), também são usadas com frequência..
Índice do artigo
- 1 Como é calculado?
- 1.1 Relação da carga axial com o estresse normal
- 2 exercícios resolvidos
- 2.1 - Exercício 1
- 2.2 - Exercício 2
- 3 referências
Como é calculado?
Para calcular o valor da carga axial nos elementos de uma estrutura, devem ser seguidos os seguintes passos:
- Faça o diagrama de força em cada elemento.
- Aplicar as equações que garantem o equilíbrio translacional, ou seja, que a soma de todas as forças seja zero.
- Considere a equação de torques ou momentos para que o equilíbrio rotacional seja satisfeito. Neste caso, a soma de todos os torques deve ser zero.
- Calcular as forças, bem como identificar as forças ou cargas axiais em cada um dos elementos.
Razão de carga axial para tensão normal
A tensão normal média é definida como a proporção da carga axial dividida pela área da seção transversal. As unidades de esforço normal no Sistema Internacional S.I. eles são Newton sobre metro quadrado (N / m²) ou Pascal (Pa). A figura 2 a seguir ilustra o conceito de tensão normal para maior clareza..
-
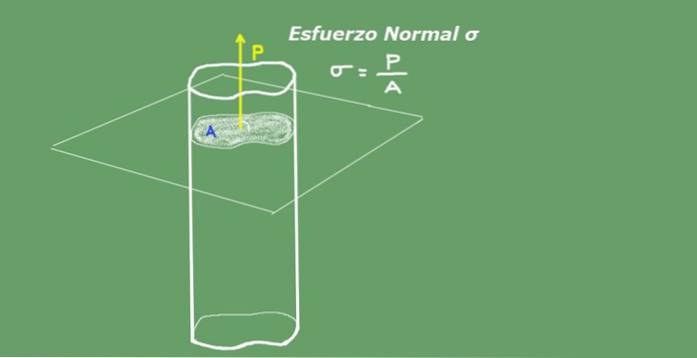
Figura 2. Tensão normal. Fonte: self made.
Exercícios resolvidos
-Exercício 1
Considere uma coluna cilíndrica de concreto de altura he raio r. Suponha que a densidade do concreto seja ρ. A coluna não suporta nenhuma carga adicional além de seu próprio peso e é apoiada em uma base retangular.
- Encontre o valor da carga axial nos pontos A, B, C e D, que estão nas seguintes posições: A na base do pilar, B a ⅓ da altura h, C a ⅔ da altura he pelo último D no o topo da coluna.
- Além disso, determine a tensão normal média em cada uma dessas posições. Tome os seguintes valores numéricos: h = 3m, r = 20cm e ρ = 2250 kg / m³
-
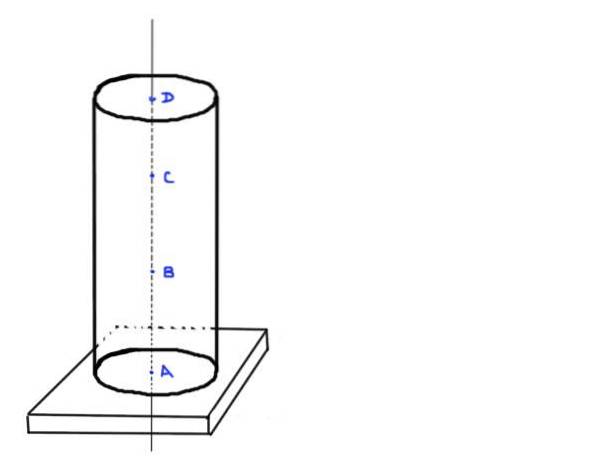
Figura 3. Coluna cilíndrica. Fonte: self made.
Solução
Peso total da coluna
O peso total W da coluna é o produto de sua densidade vezes o volume multiplicado pela aceleração da gravidade:
W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 N
Carga axial em A
No ponto A, a coluna deve suportar todo o seu peso, de modo que a carga axial neste ponto de compressão seja igual ao peso da coluna:
PA = W = 8313 N
Carga axial em B
Apenas ⅔ do pilar estará no ponto B, então a carga axial naquele ponto será de compressão e seu valor ⅔ o peso do pilar:
PB = ⅔ W = 5542 N
Figura 3. Coluna cilíndrica. Fonte: self made.
Acima da posição C há apenas ⅓ de coluna, de modo que sua carga axial de compressão será de ⅓ de seu próprio peso:
PC = ⅓ W = 2771 N
Carga axial em D
Finalmente, não há carga no ponto D, que é a extremidade superior do pilar, então a força axial naquele ponto é zero..
PD = 0 N
Esforços normais em cada uma das posições
Para determinar a tensão normal em cada uma das posições, será necessário calcular a seção transversal da área A, que é dada por:
A = π ∙ r² = 0,126m²
Desta forma, a tensão normal em cada uma das posições será o quociente entre a força axial em cada um dos pontos dividido pela área da seção transversal já calculada, que neste exercício é igual para todos os pontos por ser um coluna cilíndrica.
σ = P / A; σA = 66,15 kPa; σB = 44,10 kPa; σC = 22,05 kPa; σD = 0,00 kPa
-Exercício 2
A figura mostra uma estrutura formada por duas barras que chamaremos de AB e CB. A barra AB é apoiada na extremidade A por um pino e na outra extremidade conectada à outra barra por outro pino B.
Da mesma forma, a barra CB é apoiada na extremidade C por meio de um pino e na extremidade B com o pino B que a conecta à outra barra. Uma força vertical ou carga F é aplicada ao pino B, conforme mostrado na figura a seguir:
-
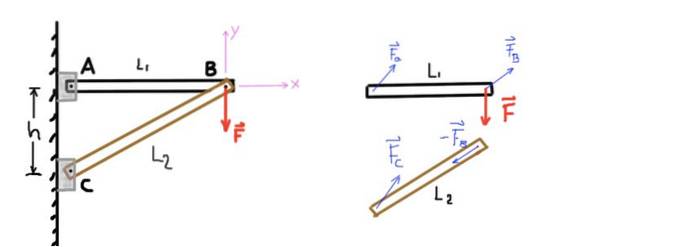
Figura 4. Estrutura de duas barras e diagrama de corpo livre. Fonte: self made.
Suponha que o peso das barras seja desprezível, uma vez que a força F = 500 kg-f é muito maior que o peso da estrutura. A separação entre os suportes A e C é h = 1,5m e o comprimento da barra AB é L1 = 2 m. Determine a carga axial em cada uma das barras, indicando se é compressão ou carga axial de tensão.
Solução 2
A figura mostra, por meio de um diagrama de corpo livre, as forças que atuam sobre cada um dos elementos da estrutura. O sistema de coordenadas cartesianas com o qual as equações de equilíbrio de forças serão estabelecidas também é indicado..
Torques ou momentos serão calculados no ponto B e serão considerados positivos se apontarem para fora da tela (eixo Z). O equilíbrio de forças e torques para cada barra é:
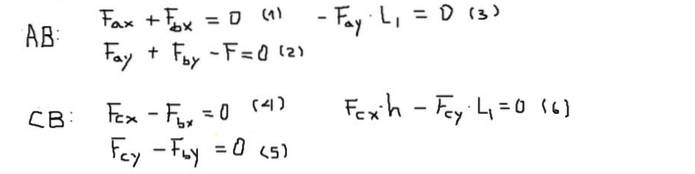
A seguir, os componentes das forças de cada uma das equações são resolvidos na seguinte ordem:
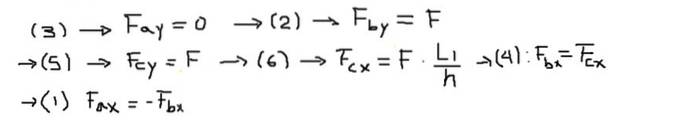
Finalmente, as forças resultantes nas extremidades de cada barra são calculadas:
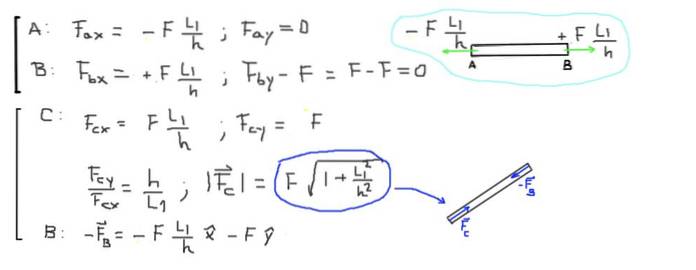
F ∙ (L1 / h) = 500 kg-f ∙ (2,0m / 1,5m) = 666,6 kg-f = 6533,3 N
A barra CB está em compressão devido às duas forças atuando em suas extremidades que são paralelas à barra e estão apontando para seu centro. A magnitude da força de compressão axial na barra CB é:
F ∙ (1 + L1² / h²) 1/2 = 500 kg-f ∙ (1 + (2 / 1,5) ²) 1/2 = 833,3 kg-f = 8166,6 N
Referências
- Cerveja F… Mecânica dos materiais. 5 ª. Edição. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Mecânica dos materiais. Oitava edição. Prentice Hall. 2011. 3-60.
- Gere J. Mecânica dos materiais. Oitava edição. Cengage Learning. 4-220.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6ª Ed. Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Notes on General Physics. UNAM. 87-98.


Ainda sem comentários