
Carga radial como calcular, exercícios resolvidos
O carga radial É a força exercida perpendicularmente ao eixo de simetria de um objeto e cuja linha de ação passa por esse eixo. Por exemplo, uma correia em uma polia impõe uma carga radial no rolamento ou rolamento do eixo da polia..
Na figura 1, as setas amarelas representam forças radiais ou cargas nos eixos devido à tensão da correia que passa pelas polias.
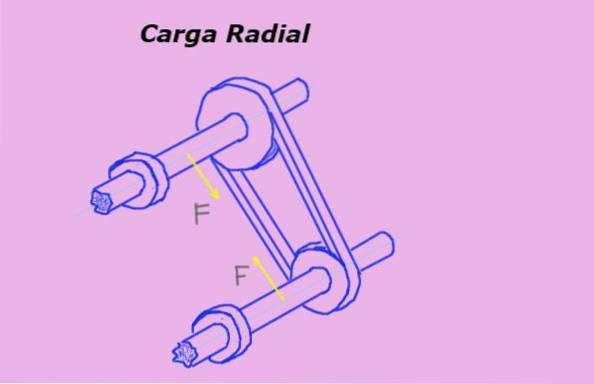
A unidade de medida para carga radial no sistema internacional ou SI é o Newton (N). Mas outras unidades de força também são freqüentemente usadas para medi-lo, como o quilograma-força (Kg-f) e a libra-força (lb-f).
Índice do artigo
- 1 Como é calculado?
- 2 exercícios resolvidos
- 2.1 - Exercício 1
- 2.2 Exercício 2
- 3 referências
Como é calculado?
Para calcular o valor da carga radial sobre os elementos de uma estrutura, devem ser seguidos os seguintes passos:
- Faça o diagrama de forças em cada elemento.
- Aplicar as equações que garantem o equilíbrio translacional; ou seja, que a soma de todas as forças é zero.
- Considere a equação de torques ou momentos para que o equilíbrio rotacional seja satisfeito. Neste caso, a soma de todos os torques deve ser zero.
- Calcule as forças para poder identificar as cargas radiais que atuam em cada um dos elementos.
Exercícios resolvidos
-Exercício 1
A figura a seguir mostra uma polia através da qual passa uma polia tensionada com tensão T. A polia é montada em um eixo sustentado por dois rolamentos. O centro de um deles está a uma distância L1 do centro da polia. Na outra extremidade está o outro rolamento, na distância Ldois.
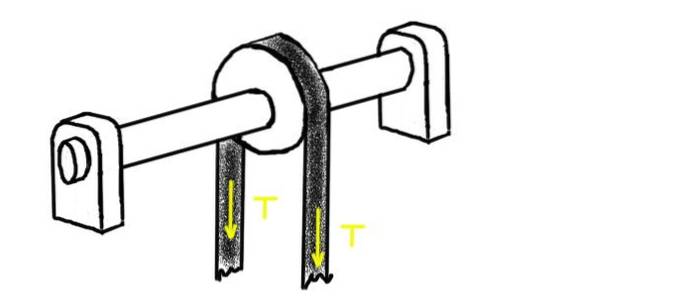
Determine a carga radial em cada um dos rolamentos, assumindo que o peso do eixo e da polia são significativamente menores do que a tensão aplicada.
Tome como valor para a tensão da correia 100 kg-fe para as distâncias L1= 1 m e Ldois= 2 m.
Solução
Em primeiro lugar, é feito um diagrama das forças que atuam no eixo.
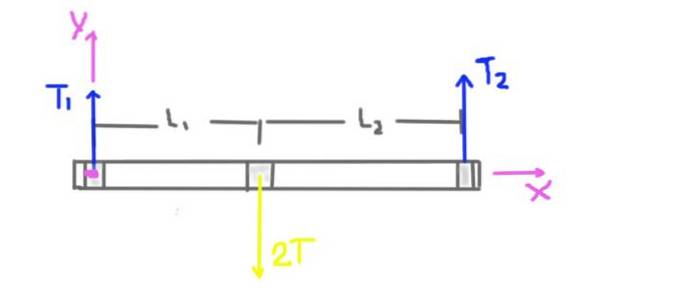
A tensão da polia é T, mas a carga radial no eixo na posição da polia é 2T. O peso do eixo e da polia não é levado em consideração porque a declaração do problema nos diz que é consideravelmente menor do que a tensão aplicada à correia.
A reação radial dos apoios no eixo é causada pelas forças radiais ou cargas T1 e T2. As distâncias L1 e L2 dos apoios ao centro da polia também estão indicadas no diagrama..
O sistema de coordenadas também é exibido. O torque ou momento total no eixo será calculado tomando como centro a origem do sistema de coordenadas e será positivo na direção Z.
Condições de equilíbrio
Agora as condições de equilíbrio estão estabelecidas: soma das forças igual a zero e soma dos torques igual a zero.
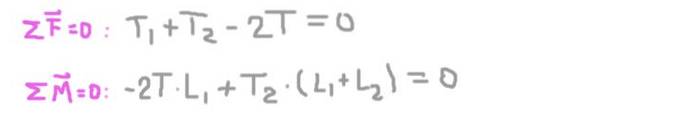
A partir da segunda equação obtemos a reação radial no eixo do suporte 2 (Tdois), substituindo no primeiro e resolvendo a reação radial no eixo no suporte 1 (T1).
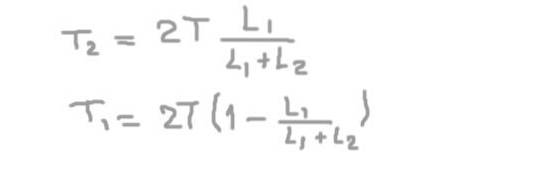
T1= (2/3) T = 66,6 kg-f
E a carga radial no eixo na posição do suporte 2 é:
Tdois= (4/3) T = 133,3 kg-f.
Exercício 2
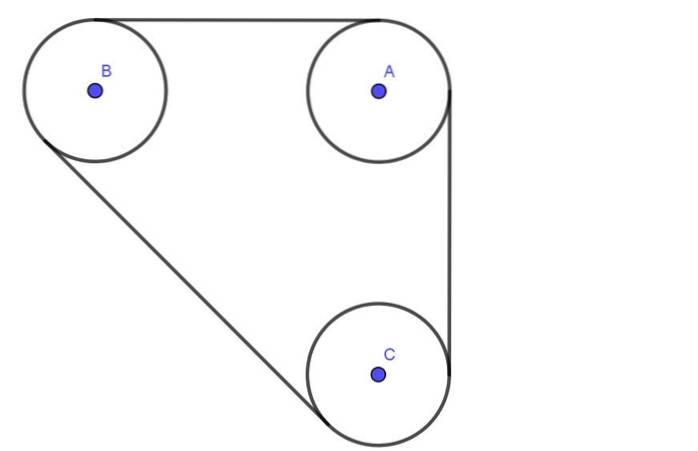
A figura a seguir mostra um sistema composto por três polias A, B, C, todas do mesmo raio R. As polias são conectadas por uma correia que possui uma tensão T.
Os eixos A, B, C passam por mancais lubrificados. A separação entre os centros dos eixos A e B é 4 vezes o raio R. Da mesma forma, a separação entre os eixos B e C também é 4R.
Determine a carga radial nos eixos das polias A e B, assumindo que a tensão da correia é 600N.
Solução
Começamos desenhando um diagrama das forças que atuam na polia A e na polia B. Na primeira temos as duas tensões T1 e Tdois, bem como a força FPARA que o rolamento exerce sobre o eixo A da polia.
Da mesma forma, na polia B, temos as tensões T3 , T4 e a força FB que o rolamento exerce sobre o eixo do mesmo. A carga radial no eixo da polia A é a força FPARA e a carga radial no B é a força FB.
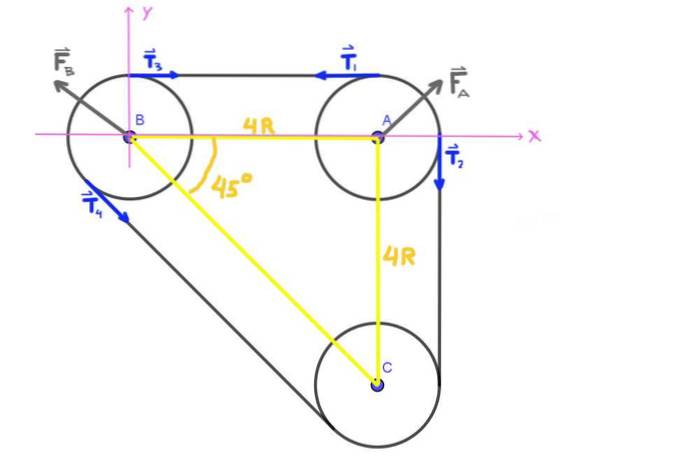
Como os eixos A, B, C formam um triângulo isorretângulo, o ângulo ABC é de 45 °.
Todas as tensões T1 , Tdois , T3 , T4 mostrado na figura tem o mesmo módulo T, que é a tensão da correia.
Condição de equilíbrio para polia A
Agora escrevemos a condição de equilíbrio para a polia A, que nada mais é do que a soma de todas as forças que atuam na polia A deve ser zero.
Separando os componentes X e Y das forças e adicionando (vetorial) o seguinte par de equações escalares é obtido:
FPARAX - T = 0; FPARAY - T = 0
Essas equações levam à seguinte igualdade: FMACHADO = FOH = T.
Portanto, a carga radial tem magnitude dada por:
FPARA = (T² + T²)1/2 = 21/2∙ T = 1,41 ∙ T = 848,5 N. com direção de 45 °.
Condição de equilíbrio para polia B
Da mesma forma, escrevemos a condição de equilíbrio para a polia B. Para o componente X, temos: FBX + T + T ∙ Cos45 ° = 0
Y para o componente Y: FBY + T ∙ Sen45 ° = 0
Desta forma:
FBX = - T (1 + 2-1/2) e FDE = -T ∙ 2-1/2
Ou seja, a magnitude da carga radial na polia B é:
FB = ((1 + 2-1/2) ² + 2-1)1/2∙ T = 1,85 ∙ T = 1108,66 N e sua direção é 135 °.
Referências
- Beer F, Johnston E, DeWolf J, Mazurek, D. Mecânica dos materiais. Quinta edição. 2010. Mc Graw Hill. 1-130.
- Gere J, Goodno, B. Mecânica dos materiais. Oitava edição. Cengage Learning. 4-220.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler R. Mecânica dos materiais. Oitava edição. Prentice Hall. 2011. 3-60.
- Valera Negrete, J. 2005. Notes on General Physics. UNAM. 87-98.



Ainda sem comentários