O célula unitária É um espaço ou região imaginária que representa a expressão mínima de um todo; que no caso da química, o todo seria um cristal composto de átomos, íons ou moléculas, que são arranjados seguindo um padrão estrutural.
Exemplos podem ser encontrados na vida cotidiana que incorporam esse conceito. Para isso, é necessário estar atento a objetos ou superfícies que apresentam certa ordem repetitiva de seus elementos. Alguns mosaicos, baixos-relevos, tectos em caixotões, folhas e papéis de parede, podem abranger em termos gerais o que se entende por célula unitária.
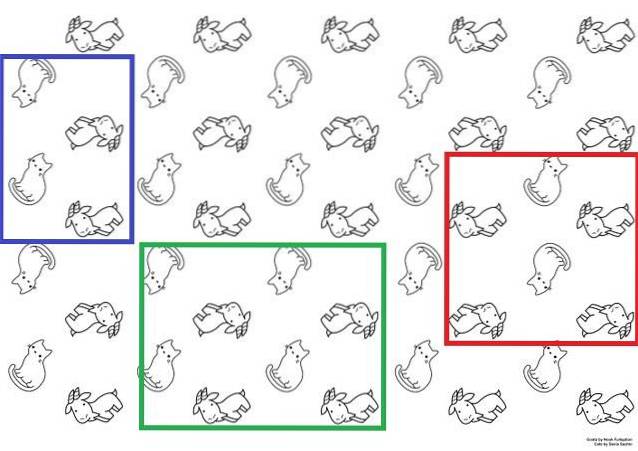
Para ilustrar com mais clareza, temos a imagem acima que pode ser usada como papel de parede. Nele, gatos e cabras aparecem com dois sentidos alternativos; os gatos ficam de pé ou de cabeça para baixo e as cabras ficam deitadas voltadas para cima ou para baixo.
Esses gatos e cabras estabelecem uma sequência estrutural repetitiva. Para construir todo o papel, bastaria reproduzir a célula unitária sobre a superfície um número suficiente de vezes, por meio de movimentos translacionais..
As células unitárias possíveis são representadas pelas caixas azul, verde e vermelha. Qualquer um desses três poderia ser usado para obter o papel; mas, é necessário movê-los imaginativamente ao longo da superfície para saber se reproduzem a mesma sequência observada na imagem..
Começando com a caixa vermelha, seria apreciado que se três colunas (de gatos e cabras) fossem movidas para a esquerda, duas cabras não apareceriam mais na parte inferior, mas apenas uma. Portanto, isso levaria a outra sequência e não pode ser considerado como uma célula unitária.
Ao passo que se eles movessem imaginativamente as duas caixas, azul e verde, a mesma sequência do papel seria obtida. Ambos são células unitárias; no entanto, a caixa azul obedece mais à definição, pois é menor que a caixa verde.
Índice do artigo
Sua própria definição, além do exemplo que acabamos de explicar, esclarece várias de suas propriedades:
-Se você se mover no espaço, independentemente da direção, obterá o sólido ou cristal completo. Isso porque, conforme mencionado com gatos e cabras, eles reproduzem a sequência estrutural; que é igual à distribuição espacial das unidades de repetição.
-Eles devem ser tão pequenos quanto possível (ou ocupar pouco volume) em comparação com outras opções de células possíveis.
-Eles geralmente são simétricos. Além disso, sua simetria é literalmente refletida nos cristais do composto; se a célula unitária de um sal é cúbica, seus cristais serão cúbicos. No entanto, existem estruturas cristalinas que são descritas com células unitárias com geometrias distorcidas..
-Eles contêm unidades repetidas, que podem ser substituídas por pontos, que por sua vez formam o que é conhecido como uma rede em três dimensões. No exemplo anterior, os gatos e cabras representam os pontos da rede, vistos de um plano superior; ou seja, duas dimensões.
As unidades de repetição ou pontos de rede das células unitárias mantêm a mesma proporção das partículas sólidas.
Se você contar o número de gatos e cabras dentro da caixa azul, terá dois gatos e cabras. O mesmo acontece com a caixa verde, e com a caixa vermelha também (mesmo que já se saiba que não é uma célula unitária).
Suponha, por exemplo, que gatos e cabras sejam átomos de G e C, respectivamente (uma estranha solda animal). Uma vez que a proporção de G para C é 2: 2 ou 1: 1 na caixa azul, pode-se esperar com segurança que o sólido terá a fórmula GC (ou CG).
Quando o sólido apresenta estruturas mais ou menos compactas, como acontece com sais, metais, óxidos, sulfetos e ligas, nas células unitárias não há unidades repetitivas inteiras; ou seja, há porções ou partes deles, que somam uma ou duas unidades.
Este não é o caso do GC. Nesse caso, a caixa azul “dividiria” os gatos e cabras em dois (1 / 2G e 1 / 2C) ou quatro (1 / 4G e 1 / 4C). Nas próximas seções, será visto que nessas células unitárias os pontos reticulares são convenientemente divididos desta e de outras maneiras..
As células unitárias no exemplo GC são bidimensionais; no entanto, isso não se aplica a modelos reais que consideram todas as três dimensões. Assim, os quadrados ou paralelogramos, são transformados em paralelepípedos. Agora, o termo "célula" faz mais sentido.
As dimensões dessas células ou paralelepípedos dependem do comprimento de seus respectivos lados e ângulos..
Na imagem inferior você tem o canto traseiro inferior do paralelepípedo, composto pelas laterais para, b Y c, e os ângulos α, β e γ.
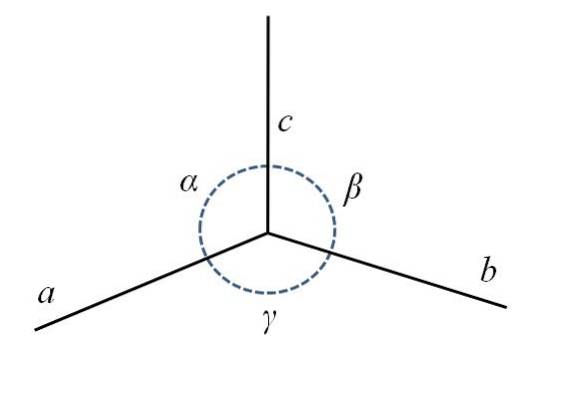
Como você pode ver, para é um pouco mais longo que b Y c. No centro há um círculo pontilhado para indicar os ângulos α, β e γ, entre ac, cb Y BA, respectivamente. Para cada célula unitária, esses parâmetros têm valores constantes e definem sua simetria e a do resto do cristal..
Aplicando um pouco de imaginação novamente, os parâmetros da imagem definiriam uma célula em forma de cubo esticada em sua borda. para. Assim, as células unitárias surgem com diferentes comprimentos e ângulos de suas bordas, que também podem ser classificadas em vários tipos.
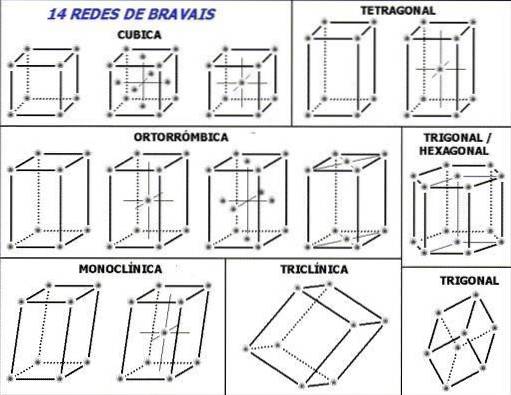
Observe para começar na imagem superior as linhas pontilhadas dentro das células unitárias: elas indicam o ângulo posterior inferior, como acabamos de explicar. A seguinte pergunta pode ser feita, onde estão os pontos da rede ou unidades repetidas? Embora dêem a impressão errada de que as células estão vazias, a resposta está em seus vértices.
Essas células são geradas ou escolhidas de forma que as unidades repetitivas (pontos acinzentados da imagem) fiquem em seus vértices. Dependendo dos valores dos parâmetros estabelecidos na seção anterior, constantes para cada célula unitária, sete sistemas de cristal são derivados.
Cada sistema de cristal tem sua própria célula unitária; o segundo define o primeiro. Na imagem superior existem sete quadrados, correspondendo aos sete sistemas de cristal; ou de uma forma um pouco mais resumida, redes cristalinas. Assim, por exemplo, uma célula unitária cúbica corresponde a um dos sistemas de cristal que define uma rede cristalina cúbica.
De acordo com a imagem, os sistemas ou redes cristalinas são:
-Cúbico
-Tetragonal
-Ortorrômbico
-Hexagonal
-Monoclínico
-Triclínico
-Trigonal
E dentro desses sistemas cristalinos surgem outros que compõem as quatorze redes Bravais; que entre todas as redes cristalinas, são as mais básicas.
Em um cubo, todos os seus lados e ângulos são iguais. Portanto, nesta célula unitária, o seguinte é verdadeiro:
para = b = c
α = β = γ = 90º
Existem três células unitárias cúbicas: simples ou primitivas, centradas no corpo (bcc) e centradas na face (fcc). As diferenças residem na forma como os pontos são distribuídos (átomos, íons ou moléculas) e no número deles.
Qual dessas células é a mais compacta? Aquele cujo volume é mais ocupado por pontos: o cúbico centrado nas faces. Observe que, se substituíssemos os pontos pelos gatos e cabras desde o início, eles não ficariam confinados a uma única célula; eles pertenceriam e seriam compartilhados por vários. Novamente, seriam porções de G ou C.
Se gatos ou cabras estivessem nos vértices, eles seriam compartilhados por 8 células unitárias; ou seja, cada célula teria 1/8 de G ou C. Junte ou imagine 8 cubos, em duas colunas de duas linhas cada, para visualizá-lo.
Se gatos ou cabras estivessem nos rostos, eles seriam compartilhados por apenas 2 células unitárias. Para vê-lo, basta colocar dois cubos juntos.
Por outro lado, se o gato ou a cabra estivessem no centro do cubo, eles pertenceriam apenas a uma única cela unitária; O mesmo acontece com as caixas da imagem principal, quando o conceito foi abordado.
Dito então o acima, dentro de uma célula unitária cúbica simples, temos uma unidade ou ponto de rede, pois possui 8 vértices (1/8 x 8 = 1). Para a célula cúbica centrada no corpo, existem: 8 vértices, que é igual a um átomo, e um ponto ou unidade no centro; portanto há dois unidades.
E para a célula cúbica centrada na face, existem: 8 vértices (1) e seis faces, onde metade de cada ponto ou unidade é compartilhada (1/2 x 6 = 3); portanto, possui quatro unidades.
Comentários semelhantes podem ser feitos em relação à célula unitária para o sistema tetragonal. Seus parâmetros estruturais são os seguintes:
para = b ≠ c
α = β = γ = 90º
Os parâmetros para a célula ortorrômbica são:
para ≠ b ≠ c
α = β = γ = 90º
Os parâmetros para a célula monoclínica são:
para ≠ b ≠ c
α = γ = 90 °; β ≠ 90º
Os parâmetros para a célula triclínica são:
para ≠ b ≠ c
α ≠ β ≠ γ ≠ 90º
Os parâmetros para a célula hexagonal são:
para = b ≠ c
α = β = 90 °; γ ≠ 120º
Na verdade, a célula constitui um terço de um prisma hexagonal.
E, finalmente, os parâmetros para a célula trigonal são:
para = b = c
α = β = γ ≠ 90º
Ainda sem comentários