
Propriedades do centro de gravidade, cálculo, exemplos
O Centro de gravidade de um corpo de tamanho mensurável é o ponto onde seu peso é considerado aplicado. É, portanto, um dos conceitos fundamentais da Estática.
A primeira abordagem nos problemas de física elementar consiste em assumir que qualquer objeto se comporta como um ponto de massa, ou seja, não tem dimensões e toda a massa está concentrada em um único ponto. Isso é válido para uma caixa, um carro, um planeta ou uma partícula subatômica. Este modelo é conhecido como modelo de partícula.

É claro que isso é uma aproximação, que funciona muito bem para muitas aplicações. Não é uma tarefa fácil considerar o comportamento individual dos milhares e milhões de partículas que qualquer objeto pode conter..
No entanto, as dimensões reais das coisas devem ser levadas em consideração, se se quiser obter resultados mais próximos da realidade. Uma vez que geralmente estamos nas proximidades da Terra, a força sempre presente em qualquer corpo é precisamente o peso.
Índice do artigo
- 1 Considerações para encontrar o centro de gravidade
- 2 Como o centro de gravidade é calculado?
- 3 propriedades
- 3.1 - Encontrar o centro de gravidade de um corpo em equilíbrio estático
- 3.2 - Exemplo resolvido
- 4 Diferença do centro de massa
- 5 exemplos de centro de gravidade
- 5.1 Centro de gravidade de objetos irregulares
- 5.2 Balanceamento de objetos
- 6 referências
Considerações para encontrar o centro de gravidade
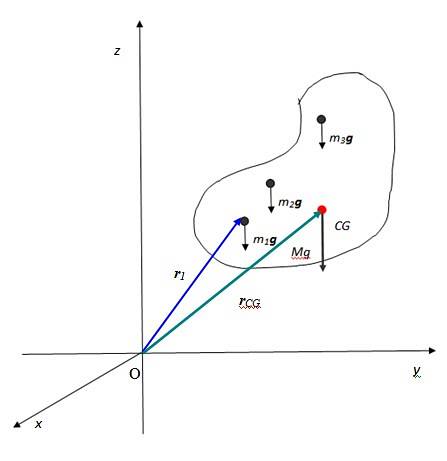
Se o tamanho do corpo for levado em consideração, onde especificamente o peso deve ser aplicado? Quando você tem um objeto arbitrariamente contínuo, seu peso é um força distribuída entre cada uma de suas partículas constituintes.
Que essas partículas sejam m1, mdois, m3... Cada um deles experimenta sua força gravitacional correspondente m1g, mdoisg, m3g…, todos eles paralelos. Isso porque o campo gravitacional da Terra é considerado constante na grande maioria dos casos, visto que os objetos são pequenos em relação ao tamanho do planeta e estão próximos de sua superfície..
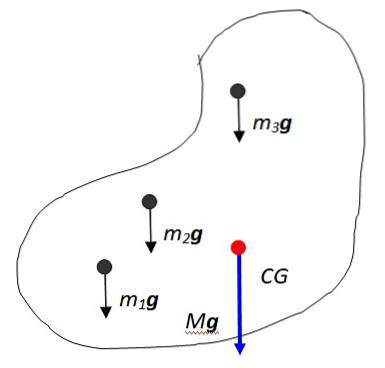
A soma vetorial dessas forças resulta no peso do objeto, aplicado ao ponto denominado centro de gravidade denotado na figura como CG, que então coincide com o Centro de massa. O centro de massa, por sua vez, é o ponto onde toda a massa pode ser considerada concentrada.
O peso resultante tem magnitude Mg Onde M é a massa total do objeto e, claro, é direcionado verticalmente para o centro da Terra. A notação de soma é útil para expressar a massa total do corpo:
O centro de gravidade nem sempre coincide com um ponto material. Por exemplo, o CG de um anel está em seu centro geométrico, onde não há massa em si. Mesmo assim, se você quiser analisar as forças que atuam em um arco, você deve aplicar o peso a este ponto preciso.
Nos casos em que o objeto tem uma forma arbitrária, se for homogêneo, seu centro de massa ainda pode ser calculado encontrando o centróide ou centro de gravidade da figura.
Como você calcula o centro de gravidade?
Em princípio, se o centro de gravidade (CG) e o centro de massa (cm) coincidem porque o campo gravitacional é uniforme, então o cm pode ser calculado e o peso aplicado a ele.
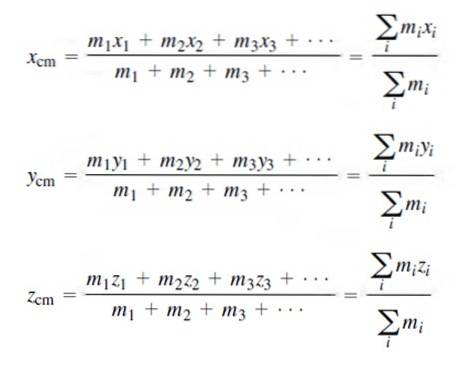
Vamos considerar dois casos: o primeiro é aquele em que a distribuição de massa é discreta; ou seja, cada massa que compõe o sistema pode ser contada e atribuída um número i, como foi feito no exemplo anterior.
As coordenadas do centro de massa para uma distribuição de massa discreta são:
Naturalmente, a soma de todas as massas é igual à massa total do sistema M, conforme indicado acima..
As três equações são reduzidas a uma forma compacta, considerando o vetor rcm ou vetor de posição do centro de massa:
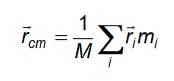
E no caso de uma distribuição de massa contínua, onde as partículas são de tamanho diferencial e não podem ser distinguidas para contá-las, a soma é substituída por uma integral que é feita sobre o volume ocupado pelo objeto em questão:
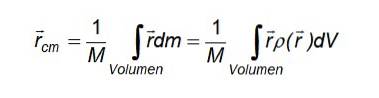
Onde r é o vetor posição de uma massa diferencial dm e a definição de densidade de massa foi usada para expressar o diferencial de massa dm contido em um diferencial de volume dV:
Propriedades
Algumas considerações importantes sobre o centro de massa são as seguintes:
- Embora seja necessário um sistema de referência para estabelecer as posições, o centro de massa não depende da escolha feita do sistema, uma vez que é uma propriedade do objeto.
- Quando o objeto tem um eixo ou plano de simetria, o centro de massa está nesse eixo ou plano. Aproveitando esta circunstância economiza tempo de cálculo.
- Todas as forças externas que atuam no objeto podem ser aplicadas ao centro de massa. Acompanhar o movimento deste ponto dá uma ideia global do movimento do objeto e facilita o trabalho de estudar seu comportamento..
-Encontrar o centro de gravidade de um corpo em equilíbrio estático
Suponha que você queira fazer com que o corpo da figura anterior esteja em equilíbrio estático, ou seja, ele não se translada ou gira em torno de um eixo de rotação arbitrário que pode ser O.

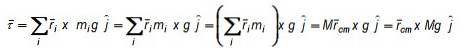
-Exemplo trabalhado
Uma barra fina de material uniforme tem 6 m de comprimento e pesa 30 N. Um peso de 50 N está pendurado em sua extremidade esquerda e um peso de 20 N está pendurado em sua extremidade direita. Encontre: a) A magnitude da força para cima necessária para manter o equilíbrio da barra, b) O centro de gravidade do conjunto.
Solução
O diagrama de força é mostrado na figura a seguir. O peso da barra é aplicado em seu centro de gravidade, que coincide com seu centro geométrico. A única dimensão da barra levada em consideração é o seu comprimento, já que o demonstrativo informa que ela é fina.
Para que o sistema bar + pesos permaneça em equilíbrio translacional, a soma das forças deve ser zero. As forças são verticais, se considerarmos para cima com sinal + e para baixo com sinal - então:
F- 50 - 20 - 30 N = 0
F = 100 N
Essa força garante o equilíbrio translacional. Tomando os momentos de torção de todas as forças em relação a um eixo que passa pela extremidade esquerda do sistema e aplicando a definição:
t = r x F
Os momentos de todas essas forças sobre o ponto selecionado são perpendiculares ao plano da barra:
tF = xF = 100x
tC = - (l / 2) mg = -3m. 30 N = -90 N.m
t1 = 0 (uma vez que a força de 50 N passa pelo eixo de rotação selecionado e não exerce momento)
tdois = -lFdois = 6 m. 20 N = -120 N.m
Portanto:
100 x -90 -120 N.m = 0
x = 2,10 m
O centro de gravidade do conjunto barra + pesos está localizado a 2,10 metros da extremidade esquerda da barra.
Diferença do centro de massa
O centro de gravidade coincide com o centro de massa, conforme indicado, desde que o campo gravitacional da Terra seja constante para todos os pontos do objeto a serem considerados. O campo gravitacional da Terra nada mais é do que o conhecido e familiar valor de g = 9,8 m / sdois dirigido verticalmente para baixo.
Embora o valor de g varie com a latitude e a altitude, eles geralmente não afetam os objetos que estão na maior parte do tempo. Seria muito diferente se você considerar um grande corpo nas proximidades da Terra, por exemplo, um asteróide que está muito perto do planeta.
O asteróide tem seu próprio centro de massa, mas seu centro de gravidade não teria mais que coincidir com este, uma vez que g provavelmente experimentaria variações substanciais em magnitude, dado o tamanho do asteróide e que os pesos de cada partícula podem não ser paralelos.
Outra diferença fundamental é que o centro de massa é encontrado independentemente de haver ou não uma força chamada peso aplicada ao objeto. É uma propriedade intrínseca do objeto que nos revela como sua massa se distribui em relação à sua geometria..
O centro de massa existe independentemente de haver ou não peso aplicado. E está localizado na mesma posição, mesmo que o objeto se mova para outro planeta no qual o campo gravitacional seja diferente..
Por outro lado, o centro de gravidade está claramente ligado à aplicação do peso, como vimos ao longo dos parágrafos anteriores..
Exemplos de centro de gravidade
Centro de gravidade de objetos irregulares
É muito fácil descobrir onde está o centro de gravidade de um objeto irregular como uma xícara. Primeiro, ele é suspenso em qualquer ponto e a partir daí uma linha vertical é desenhada (na figura 5 é a linha fúcsia na imagem à esquerda).
Ela é então suspensa em outro ponto e uma nova vertical é desenhada (linha turquesa na imagem da direita). A intersecção de ambas as linhas é o centro de gravidade do copo.

Objetos de equilíbrio
Vamos analisar a estabilidade de um caminhão viajando na estrada. Quando o centro de gravidade está acima da base do caminhão, o caminhão não tomba. A imagem à esquerda é a posição mais estável.
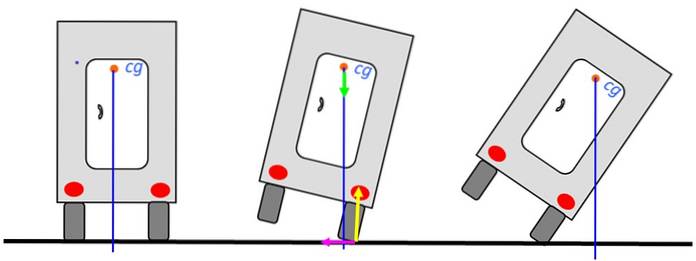
Mesmo quando o caminhão estiver inclinado para a direita, ele poderá retornar a uma posição de equilíbrio estável, como no desenho do meio, já que a vertical ainda passa pela base. No entanto, quando esta linha passa para fora, o caminhão capota.
O diagrama mostra as forças no ponto de apoio: normal em amarelo, peso em verde e atrito estático à esquerda em fúcsia. A normal e a fricção são aplicadas no eixo de rotação, portanto, não exercem torque. Portanto, eles não contribuirão para capotar o caminhão.
O peso permanece, o que exerce um torque, felizmente no sentido anti-horário e que tende a retornar o caminhão à sua posição de equilíbrio. Observe que a linha vertical passa pela superfície de apoio, que é o pneu.
Quando o caminhão está na posição mais à direita, o torque do peso muda para sentido horário. Incapaz de ser combatido em outro momento, o caminhão capotará.
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill. 247-253.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º… Ed Prentice Hall. 229-238.
- Resnick, R. (1999). Fisica. Vol. 1. 3ª Ed. Em espanhol. Compañía Editorial Continental S.A. de C.V. 331-341.
- Rex, A. 2011. Fundamentals of Physics. Pearson. 146-155.
- Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1.340-346.



Ainda sem comentários