Choques elásticos em uma dimensão, casos especiais, exercícios

O choques elásticos ou colisões elásticas consistem em interações breves, mas intensas entre objetos, nas quais tanto o momento quanto a energia cinética são conservados. Os acidentes são eventos muito frequentes na natureza: de partículas subatômicas a galáxias, a bolas de bilhar e carrinhos de choque em parques de diversões, são todos objetos capazes de colidir.

Durante uma colisão ou colisão, as forças de interação entre os objetos são muito fortes, muito mais do que aquelas que podem agir externamente. Desta forma, pode-se afirmar que durante a colisão, as partículas formam um sistema isolado.

Nesse caso, é verdade que:

P_ou = P_F

A quantidade de movimento P_ou antes da colisão é o mesmo que depois da colisão. Isso é verdadeiro para qualquer tipo de colisão, tanto elástica quanto inelástica..

Agora considere o seguinte: durante uma colisão, os objetos sofrem uma certa deformação. Quando o choque é elástico, os objetos recuperam rapidamente sua forma original.

Índice do artigo

• 1 Conservação de energia cinética
• 2 choques elásticos em uma dimensão
  • 2.1 - Fórmulas para colisões elásticas
• 3 casos especiais em colisões elásticas
  • 3.1 Duas massas idênticas
  • 3.2 Duas massas idênticas, uma das quais estava inicialmente em repouso
  • 3.3 Duas massas diferentes, uma delas inicialmente em repouso
• 4 Coeficiente de restituição ou regra de Huygens-Newton
• 5 exercícios resolvidos
  • 5.1 - Exercício resolvido 1
  • 5.2 - Exercício resolvido 2
  • 5.3 - Exercício resolvido 3
  • 5.4 - Exercício 4 resolvido
• 6 referências

Conservação de energia cinética

Normalmente, durante uma colisão, parte da energia dos objetos é gasta em calor, deformação, som e às vezes até na produção de luz. Portanto, a energia cinética do sistema após a colisão é menor do que a energia cinética original.

Quando a energia cinética K é conservada, então:

K_ou = K_F

O que significa que as forças que atuam durante a colisão são conservadoras. Durante a colisão, a energia cinética é brevemente transformada em energia potencial e depois de volta em energia cinética. As respectivas energias cinéticas variam, mas a soma permanece constante.

As colisões perfeitamente elásticas são raras, embora as bolas de bilhar sejam uma aproximação bastante boa, assim como as colisões que ocorrem entre as moléculas de gás ideais..

Choques elásticos em uma dimensão

Vamos examinar uma colisão de duas partículas disso em uma única dimensão; ou seja, as partículas interagentes se movem, digamos, ao longo do eixo x. Suponha que eles tenham massas m₁ Y m_dois. As velocidades iniciais de cada um são ou₁ Y ou_dois respectivamente. As velocidades finais são v₁ Y v_dois.

Podemos dispensar a notação vetorial, uma vez que o movimento é realizado ao longo do eixo x, porém os sinais (-) e (+) indicam a direção do movimento. À esquerda é negativo e à direita positivo, por convenção.

-Fórmulas para colisões elásticas

Pela quantidade de movimento

m₁ou₁ + m_doisou_dois = m₁v₁ + m_doisv_dois

Para energia cinética

½ m₁ou^dois₁ + ½ m_doisou^dois_dois = ½ m₁v^dois₁ +  ½ m_doisv^dois_dois

Desde que as massas e velocidades iniciais sejam conhecidas, as equações podem ser reagrupadas para encontrar as velocidades finais.

O problema é que, em princípio, é necessário fazer um pouco de álgebra tediosa, já que as equações da energia cinética contêm os quadrados das velocidades, o que torna o cálculo um pouco complicado. O ideal seria encontrar expressões que não os contenham.

A primeira coisa é prescindir do fator ½ e reorganizar as duas equações de forma que apareça um sinal negativo e as massas possam ser fatoradas:

m₁ou₁ - m₁v₁ = M_doisv_dois - m_doisou_dois

m₁ou^dois₁ - m₁v^dois₁  = + M_doisv^dois_dois - m_doisou^dois_dois

Sendo expresso desta forma:

m₁(ou₁ - v₁ ) = m_dois(v_dois - ou_dois)

m₁(ou^dois₁ - v^dois₁ ) = m_dois (v^dois_dois - ou^dois_dois)

Simplificação para eliminar os quadrados das velocidades

Agora devemos nos valer da soma notável do produto por sua diferença na segunda equação, com a qual obtemos uma expressão que não contém os quadrados, como originalmente desejado:

m₁(ou₁ - v₁ ) = m_dois(v_dois - ou_dois)

m₁(ou₁ - v₁ ) (ou₁ + v₁ ) = m_dois (v_dois - ou_dois) (v_dois + ou_dois)

A próxima etapa é substituir a primeira equação pela segunda:

m_dois(v_dois - ou_dois) (ou₁ + v₁ ) = m_dois (v_dois - ou_dois) (v_dois + ou_dois)

E quando o termo é repetido m_dois(v_dois - ou_dois) em ambos os lados da igualdade, o referido termo é cancelado e tem a seguinte aparência:

(ou₁ + v₁) = (v_dois + ou_dois)

Ou melhor ainda:

ou₁ - ou_dois= v_dois -  v₁

Velocidades finais v₁ e V_dois das partículas

Agora você tem duas equações lineares que são mais fáceis de trabalhar. Vamos colocá-los de volta um abaixo do outro:

m₁ou₁ + m_doisou_dois = m₁v₁ + m_doisv_dois

ou₁ - ou_dois= v_dois -  v₁

Multiplicando a segunda equação por m₁ e adicionar termo a termo é:

m₁ou₁ + m_doisou_dois = m₁v₁ + m_doisv_dois

m₁ou₁ - m₁ou_dois= m₁v_dois - m₁ v₁

-

2 m₁ou₁ + (m_dois - m₁) ou_dois = (m_dois + m₁) v_dois

E já é possível limpar v_dois. Por exemplo:

Casos especiais em colisões elásticas

Agora que as equações estão disponíveis para as velocidades finais de ambas as partículas, é hora de analisar algumas situações especiais.

Duas massas idênticas

Nesse caso m₁ = m_dois = m Y:

v₁ = u_dois

v_dois = u₁

As partículas simplesmente trocam suas velocidades após a colisão.

Duas massas idênticas, uma das quais estava inicialmente em repouso

De novo  m₁ = m_dois = m e assumindo que ou₁ = 0:

v₁ = u_dois

v_dois = 0

Após a colisão, a partícula que estava em repouso adquire a mesma velocidade da partícula que estava se movendo, e esta por sua vez para.

Duas massas diferentes, uma delas inicialmente em repouso

Neste caso, suponha que ou₁ = 0, mas as massas são diferentes:

Que passa sim m₁ é muito maior que m_dois?

Acontece que m₁ ainda está em repouso e m_dois retorna tão rápido quanto bateu.

Coeficiente de restituição ou regra de Huygens-Newton

Anteriormente, a seguinte relação entre as velocidades era derivada para dois objetos em colisão elástica: ou₁ - ou_dois = v_dois -  v₁. Essas diferenças são as velocidades relativas antes e depois da colisão. Em geral, para uma colisão, é verdade que:

ou₁ - ou_dois = - (v₁ -  v_dois)

O conceito de velocidade relativa é melhor apreciado se o leitor imaginar que está em uma das partículas e, a partir dessa posição, observar a velocidade com que a outra partícula se move. A equação acima foi reescrita assim:

Exercícios resolvidos

-Exercício 1 resolvido

Uma bola de bilhar está se movendo para a esquerda a 30 cm / s, colidindo de frente com outra bola idêntica se movendo para a direita a 20 cm / s. As duas bolas têm a mesma massa e a colisão é perfeitamente elástica. Encontrando a velocidade de cada bola após o impacto.

Solução

ou₁ = -30 cm / s

ou_dois = +20 cm / s

É o caso especial em que duas massas idênticas colidem elasticamente em uma dimensão, portanto as velocidades são trocadas.

v₁ = +20 cm / s

v_dois = -30 cm / s

-Exercício resolvido 2

O coeficiente de restituição de uma bola que quica no solo é igual a 0,82. Se cair do repouso, que fração de sua altura original a bola alcançará depois de quicar uma vez? E depois de 3 saltos?

Solução

O solo pode ser o objeto 1 na equação do coeficiente de restituição. E fica sempre em repouso, para que:

Com esta velocidade, ele salta:

O sinal + indica que é uma velocidade ascendente. E de acordo com ele, a bola atinge uma altura máxima de:

Agora ele retorna ao solo novamente com uma velocidade da mesma magnitude, mas o sinal oposto:

Isso atinge uma altura máxima de:

Volte para o solo com:

Saltos sucessivos

Cada vez que a bola quica e sobe, multiplique a velocidade novamente por 0,82:

Agora h₃ é cerca de 30% de h_ou. Qual seria a altura para o 6º salto sem a necessidade de fazer cálculos detalhados como os anteriores?

Seria h₆ = 0,82¹² h_ou = 0,092h_ou ou apenas 9% de h_ou.

-Exercício resolvido 3

Um bloco de 300 g está se movendo para o norte a 50 cm / se colide com um bloco de 200 g indo para o sul a 100 cm / s. Suponha que o choque seja perfeitamente elástico. Encontre as velocidades após o impacto.

Dados

m₁ = 300 g; ou₁ = + 50 cm / s

m_dois = 200 g; ou_dois = -100 cm / s

-Exercício resolvido 4

Uma massa de m é liberada₁ = 4 kg a partir do ponto indicado na pista sem atrito, até que colida com m_dois = 10 kg em repouso. Quão alto me sobe?₁ depois da colisão?

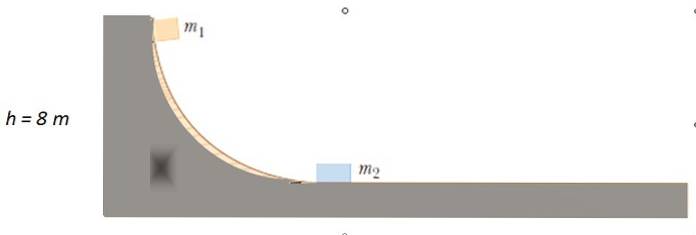
Solução

Uma vez que não há atrito, a energia mecânica é conservada para encontrar a velocidade ou₁ com que m₁ impactos  m_dois. Inicialmente a energia cinética é 0, uma vez que m₁ parte do resto. Quando ele se move na superfície horizontal, ele não tem altura, então a energia potencial é 0.

mgh = ½ mu₁ ^dois

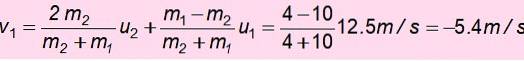
ou_dois = 0

Agora, a velocidade de m₁ após a colisão:

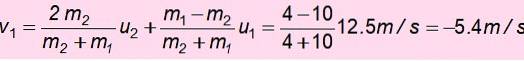
O sinal negativo significa que foi devolvido. Com esta velocidade ele aumenta e a energia mecânica é conservada novamente para encontrar h ', a altura à qual você pode subir após a queda:

½ mv₁^dois = mgh '

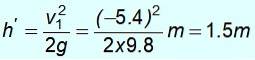
Observe que ele não retorna ao ponto inicial a uma altitude de 8 m. Não tem energia suficiente porque a massa deu parte de sua energia cinética m_1.

Referências

1. Giancoli, D. 2006. Física: Princípios com Aplicações. 6^º. Ed Prentice Hall. 175-181
2. Rex, A. 2011. Fundamentals of Physics. Pearson. 135-155.
3. Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9^{n / D} Cengage Learning. 172-182
4. Tipler, P. (2006) Physics for Science and Technology. 5ª Ed. Volume 1. Editorial Reverté. 217-238
5. Tippens, P. 2011. Physics: Concepts and Applications. 7ª Edição. MacGraw Hill. 185-195