Como encontrar o ângulo de um triângulo?

Existem várias maneiras de calcular os lados e ângulos de um triângulo. Isso depende do tipo de triângulo com o qual você está trabalhando.

Nesta oportunidade, será mostrado como calcular os lados e ângulos de um triângulo retângulo, assumindo que certos dados do triângulo são conhecidos.

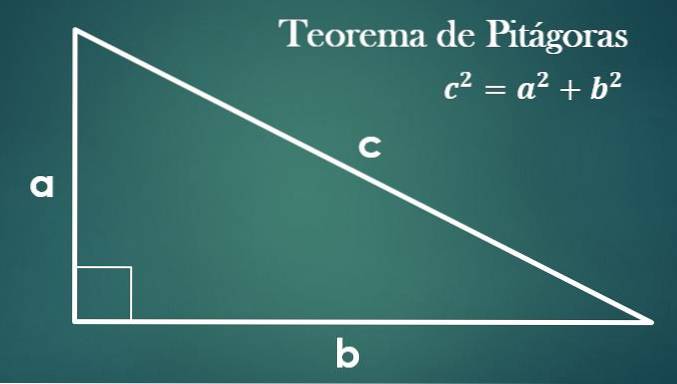
Os elementos que serão usados ​​são:

- O teorema de Pitágoras

Dado um triângulo retângulo com pernas "a", "b" e hipotenusa "c", é verdade que "c² = a² + b²".

- Área de um triângulo

A fórmula para calcular a área de qualquer triângulo é A = (b × h) / 2, onde “b” é o comprimento da base e “h” é o comprimento da altura.

- Ângulos de um triângulo

A soma dos três ângulos internos de um triângulo é 180º.

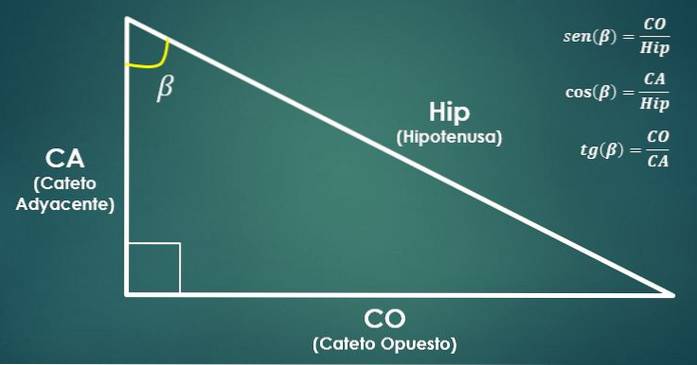
- Funções trigonométricas:

Considere um triângulo retângulo. Então, as funções trigonométricas seno, cosseno e tangente do ângulo beta (β) são definidas como segue:

sin (β) = CO / Hip, cos (β) = CA / Hip e tan (β) = CO / CA.

Como encontrar os lados e ângulos de um triângulo retângulo?

Dado um triângulo retângulo ABC, as seguintes situações podem ocorrer:

1- As duas pernas são conhecidas

Se a perna “a” mede 3 cm e a perna “b” mede 4 cm, então o teorema de Pitágoras é usado para calcular o valor de “c”. Substituindo os valores de "a" e "b" obtemos que c² = 25 cm², o que implica que c = 5 cm.

Agora, se o ângulo β é oposto à perna “b”, então sin (β) = 4/5. Aplicando a função inversa do seno, nesta última igualdade obtemos que β = 53,13º. Dois ângulos internos do triângulo já são conhecidos.

Seja θ o ângulo que falta saber, então 90º + 53,13º + θ = 180º, do qual obtemos que θ = 36,87º.

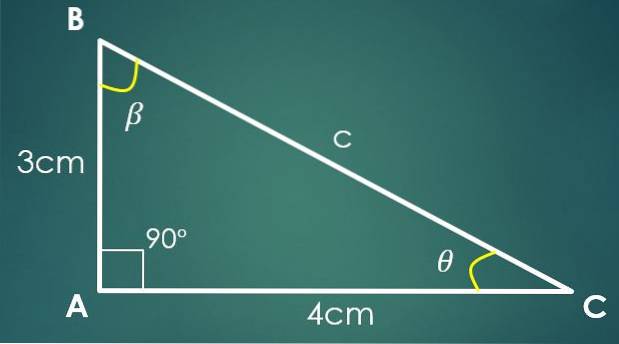
Neste caso, não é necessário que os lados conhecidos sejam as duas pernas, o importante é saber o valor de quaisquer dois lados.

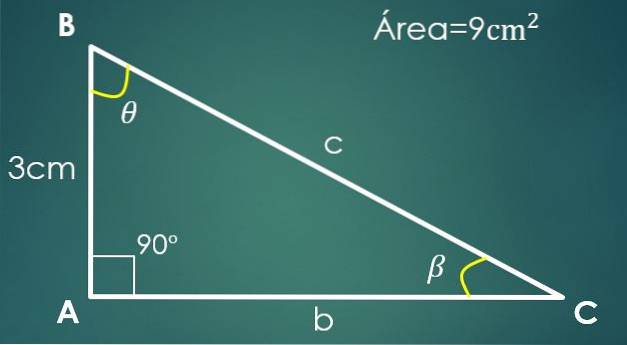
2- Uma perna é conhecida e a área

Seja a = 3 cm a perna conhecida e A = 9 cm² a área do triângulo.

Em um triângulo retângulo, uma perna pode ser considerada a base e a outra a altura (já que são perpendiculares).

Suponha que “a” seja a base, portanto 9 = (3 × h) / 2, de onde obtemos que a outra perna tem 6 cm. Para calcular a hipotenusa, proceda como no caso anterior, e obtemos que c = √45 cm.

Agora, se o ângulo β é oposto à perna “a”, então sin (β) = 3 / √45. Resolvendo para β obtém-se que seu valor é 26,57º. Precisamos apenas saber o valor do terceiro ângulo θ.

Está satisfeito que 90º + 26,57º + θ = 180º, a partir do qual se conclui que θ = 63,43º.

3- Um ângulo e uma perna são conhecidos

Seja β = 45º o ângulo conhecido e a = 3 cm a perna conhecida, onde a perna “a” é o ângulo oposto β. Usando a fórmula da tangente, obtemos que tg (45º) = 3 / CA, da qual segue que CA = 3 cm.

Usando o teorema de Pitágoras obtém-se que c² = 18 cm², ou seja, c = 3√2 cm.

Sabe-se que um ângulo mede 90º e que β mede 45º, daqui conclui-se que o terceiro ângulo mede 45º..

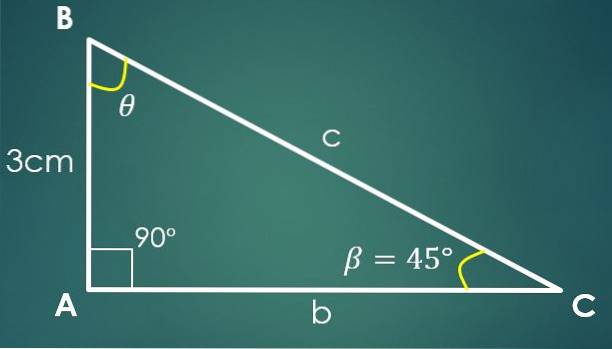
Neste caso, o lado conhecido não precisa ser uma perna, pode ser qualquer um dos três lados do triângulo.

Referências

1. Landaverde, F. d. (1997). Geometria (Reimpressão ed.). Progresso.
2. Leake, D. (2006). Triângulos (edição ilustrada). Heinemann-Raintree.
3. Pérez, C. D. (2006). Pré-cálculo. Pearson Education.
4. Ruiz, Á., & Barrantes, H. (2006). Geometrias. Tecnologia CR.
5. Sullivan, M. (1997). Pré-cálculo. Pearson Education.
6. Sullivan, M. (1997). Trigonometria e geometria analítica. Pearson Education.