Fórmulas de coeficiente de correlação, cálculo, interpretação, exemplo

O coeficiente de correlação nas estatísticas é um indicador que mede a tendência de duas variáveis ​​quantitativas X e Y terem uma relação linear ou proporcional entre elas..

Geralmente, os pares de variáveis ​​X e Y são duas características da mesma população. Por exemplo, X pode ser a altura de uma pessoa e Y seu peso..

Nesse caso, o coeficiente de correlação indicaria se há ou não tendência de relação proporcional entre altura e peso em uma determinada população..

O coeficiente de correlação linear de Pearson é denotado pela letra r letras minúsculas e seus valores mínimo e máximo são -1 e +1, respectivamente. 

Um valor r = +1 indicaria que o conjunto de pares (X, Y) está perfeitamente alinhado e que quando X crescer, Y crescerá na mesma proporção. Por outro lado, se r = -1, o conjunto de pares também ficaria perfeitamente alinhado, mas neste caso quando X aumenta, Y diminui na mesma proporção.

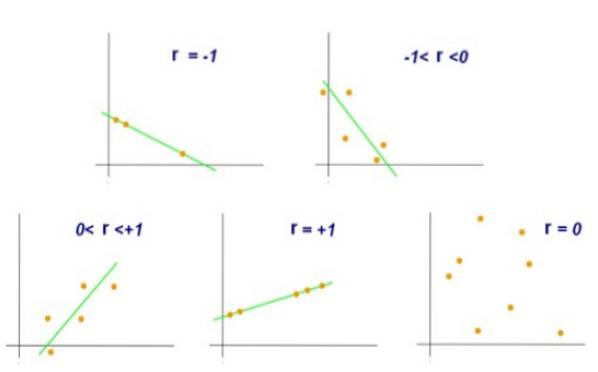
Por outro lado, um valor de r = 0 indicaria que não há correlação linear entre as variáveis ​​X e Y. Enquanto um valor de r = +0,8 indicaria que os pares (X, Y) tendem a se agrupar em um lado e outro de certo direto.

A fórmula para calcular o coeficiente de correlação r é a seguinte:

Como calcular o coeficiente de correlação?

O coeficiente de correlação linear é uma quantidade estatística encontrada em calculadoras científicas, na maioria das planilhas e programas estatísticos..

Porém, é conveniente saber como se aplica a fórmula que a define, e para isso será mostrado um cálculo detalhado, realizado em um pequeno conjunto de dados..

E como foi dito na seção anterior, o coeficiente de correlação é a covariância Sxy dividida pelo produto do desvio padrão Sx para as variáveis ​​X e Sy para a variável Y.

Covariância e variância

A covariância Sxy é:

Sxy = [Σ (Xi - ) (Yi - )] / (N-1)

Onde a soma vai de 1 para os N pares de dados (Xi, Yi). e são as médias aritméticas dos dados Xi e Yi respectivamente.

Por sua vez, o desvio padrão para a variável X é a raiz quadrada da variância do conjunto de dados Xi, com i de 1 a N:

Sx = √ [Σ (Xi - ) ^ 2) / (N-1)]

Da mesma forma, o desvio padrão para a variável Y é a raiz quadrada da variância do conjunto de dados Yi, com i de 1 a N:

Sy = √ [Σ (Yi - )^dois ) / (N-1)]

Caso ilustrativo

A fim de mostrar em detalhes como calcular o coeficiente de correlação, tomaremos o seguinte conjunto de quatro pares de dados 

(X, Y): (1, 1); (2,3); (3, 6) e (4, 7).

Primeiro, calculamos a média aritmética para X e Y, como segue:

= (1 + 2 + 3 + 4) / 4 = 2,5

= (1 + 3 + 6 + 7) / 4 = 4,25

Em seguida, os parâmetros restantes são calculados:

Covariância Sxy

Sxy = [(1 - 2,5) (1 - 4,25) + (2 - 2,5) (3 - 4,25) + (3 - 2,5) (6 - 4,25) +….…. (4 - 2,5) (7 - 4,25) ] / (4-1)

Sxy = [(-1,5) (- 3,25) + (-0,5) (- 1,25) + (0,5) (1,75) +… . 

…. (1,5) (2,75)] / (3) = 10,5 / 3 = 3,5

Desvio padrão Sx

Sx = √ [(-1,5)^dois + (-0,5)^dois + (0,5)^dois + (1,5)^dois) / (4-1)] = √ [5/3] = 1,29

Desvio padrão Sy

Sx = √ [(-3,25)^dois + (-1,25)^dois + (1,75)^dois + (2,75)^dois) / (4-1)] = 

√ [22,75 / 3] = 2,75

Coeficiente de correlação r

r = 3,5 / (1,29 * 2,75) = 0,98

Interpretação

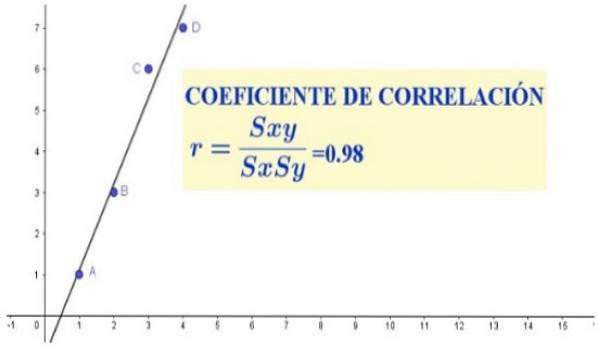
No conjunto de dados do caso anterior, observa-se uma forte correlação linear entre as variáveis ​​X e Y, que se manifesta tanto no gráfico de dispersão (mostrado na Figura 1) quanto no coeficiente de correlação, que gerou um valor bastante próximo da unidade.

Na medida em que o coeficiente de correlação está mais próximo de 1 ou -1, mais sentido faz o ajuste dos dados a uma linha, o resultado da regressão linear..

Regressão linear

A linha de regressão linear é obtida a partir de Método dos mínimos quadrados. em que os parâmetros da reta de regressão são obtidos a partir da minimização da soma do quadrado da diferença entre o valor estimado de Y e o Yi dos N dados.

Por outro lado, os parâmetros aeb da linha de regressão y = a + bx, obtidos pelo método dos mínimos quadrados, são:

* b = Sxy / (Sx^dois) Para a inclinação

* a = - b para a interseção da linha de regressão com o eixo Y.

Lembre-se de que Sxy é a covariância definida acima e Sx^dois é a variância ou quadrado do desvio padrão definido acima. e são as médias aritméticas dos dados X e Y respectivamente.

Exemplo

O coeficiente de correlação é usado para determinar se existe uma correlação linear entre duas variáveis. É aplicável quando as variáveis ​​a serem estudadas são quantitativas e, além disso, assume-se que seguem uma distribuição do tipo normal..

Temos um exemplo ilustrativo a seguir: uma medida do grau de obesidade é o índice de massa corporal, que é obtido dividindo-se o peso de uma pessoa em quilogramas pela altura ao quadrado da mesma em unidades de metros ao quadrado.

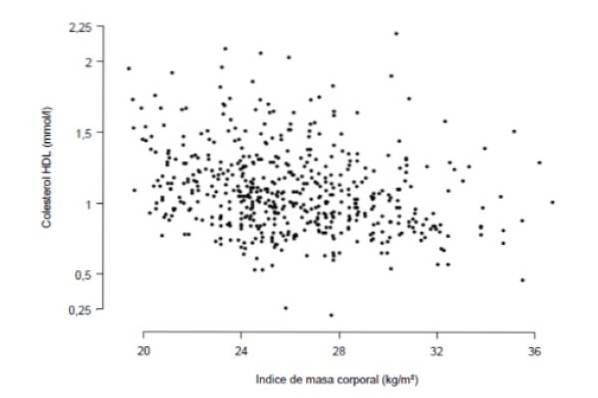
Você quer saber se existe uma forte correlação entre o índice de massa corporal e a concentração de colesterol HDL no sangue, medida em milimoles por litro. Para tanto, foi realizado um estudo com 533 pessoas, que se resume no gráfico a seguir, em que cada ponto representa os dados de uma pessoa.

A observação cuidadosa do gráfico mostra que existe uma certa tendência linear (não muito acentuada) entre a concentração de colesterol HDL e o índice de massa corporal. A medida quantitativa dessa tendência é o coeficiente de correlação, que para este caso acabou sendo r = -0,276.

Referências

1. González C. Estatísticas Gerais. Recuperado de: tarwi.lamolina.edu.pe
2. IACS. Instituto Aragonês de Ciências da Saúde. Recuperado de: ics-aragon.com 
3. Salazar C. e Castillo S. Princípios básicos de estatística. (2018). Recuperado de: dspace.uce.edu.ec
4. Superprof. Coeficiente de correlação. Recuperado de: superprof.es
5. USAC. Manual de estatísticas descritivas. (2011). Recuperado de: statistics.ingenieria.usac.edu.gt
6. Wikipedia. Coeficiente de correlação de Pearson. Recuperado de: es.wikipedia.com.