
Coeficiente de conceito de restituição, fórmula, cálculo, exemplo

O coeficiente de restituição é o quociente entre a velocidade relativa de recuo e a velocidade relativa de aproximação de dois corpos em colisão. Quando os corpos são unidos após a colisão, esse quociente é zero. E a unidade vale no caso em que a colisão seja perfeitamente elástica.
Suponha que duas esferas sólidas de massa M1 e massa M2 respectivamente que sofrem uma colisão. Pouco antes da colisão, as esferas tinham velocidades V1 Y V2 com respeito a um certo sistema de referência inercial. Logo após a colisão, suas velocidades mudam para V1 ' Y V2 '.
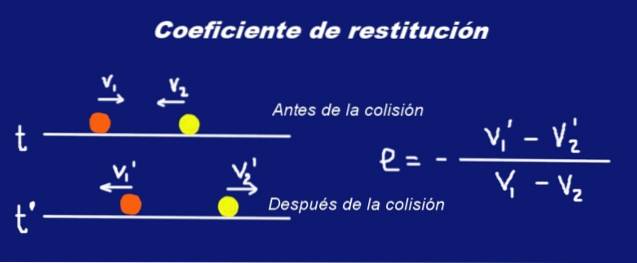
A carta foi colocada negrito nas velocidades para indicar que são quantidades vetoriais.
Experimentos indicam que cada colisão cumpre a seguinte relação:
V1 ' - V2 '= -e (V1 - V2)
Onde e é um número real entre 0 e 1, chamado de coeficiente de restituição da colisão. A expressão acima é interpretada assim:
A velocidade relativa de duas partículas antes da colisão é proporcional à velocidade relativa das duas partículas após a colisão, a constante de proporcionalidade é (-e), onde e é o coeficiente de restituição da colisão.
Índice do artigo
- 1 Qual é o coeficiente de restituição para?
- 1.1 O momento
- 1.2 Energia e coeficiente de restituição
- 2 Como é calculado o coeficiente de restituição?
- 3 exemplo
- 3.1 Solução
- 4 referências
Qual é o coeficiente de restituição para?
A utilidade deste coeficiente reside em conhecer o grau de inelasticidade de uma colisão. No caso em que a colisão é perfeitamente elástica, o coeficiente será 1, enquanto em uma colisão totalmente inelástica o coeficiente será 0, pois neste caso a velocidade relativa após a colisão é zero..
Por outro lado, se o coeficiente de restituição de uma colisão e as velocidades das partículas antes dela forem conhecidas, então as velocidades após a ocorrência da colisão podem ser previstas..
Momentum
Nas colisões, além da relação que estabelece o coeficiente de restituição, existe outra relação fundamental, que é a conservação de momentum.
Momentum p de uma partícula, ou momento, como também é chamado, é o produto da massa M da partícula por sua velocidade V. Quer dizer: o momentum p é uma quantidade vetorial.
Em colisões, o momento linear P do sistema é o mesmo antes e logo após a colisão, porque as forças externas são insignificantes em comparação com as forças breves, mas intensas de interação interna durante a colisão. Mas a conservação do momento não é suficiente P do sistema para resolver o problema geral de colisão.
No caso mencionado anteriormente, o das duas esferas em colisão de massas M1 e M2, a conservação do momento linear é escrita da seguinte forma:
M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .
Não há como resolver o problema da colisão se o coeficiente de restituição não for conhecido. A conservação do momento, embora necessária, é insuficiente para prever as velocidades após a colisão.
Quando um problema afirma que os corpos permanecem se movendo juntos após a colisão, isso implicitamente diz que o coeficiente de restituição é 0.

Energia e coeficiente de restituição
A outra quantidade física importante envolvida nas colisões é a energia. Durante as colisões, ocorrem trocas de energia cinética, energia potencial e outros tipos de energia, como energia térmica.
Antes e depois da colisão, a energia potencial de interação é praticamente zero, então o balanço de energia envolve a energia cinética das partículas antes e depois e uma quantidade Q chamada energia dissipada.
Para as duas esferas de massa em colisão M1 e M2, o balanço de energia antes e depois da colisão é escrito da seguinte forma:
½ M1 V1^ 2 + ½ M2 V2^ 2 = ½ M1 V1 '^ 2 + ½ M2 V2 '^ 2 + Q
Quando as forças de interação durante a colisão são puramente conservadoras, acontece que o energia cinética total das partículas em colisão é conservado, ou seja, é o mesmo antes e depois da colisão (Q = 0). Quando isso acontece, a colisão é considerada perfeitamente elástica..
Em casos de colisões elásticas, nenhuma energia é dissipada. E, além disso, o coeficiente de restituição está em conformidade com: e = 1.
Pelo contrário, nas colisões inelásticas Q ≠ 0 e 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.
Para que um problema de colisão seja perfeitamente determinado, é necessário conhecer o coeficiente de restituição, ou alternativamente a quantidade de energia dissipada durante a colisão.
O coeficiente de restituição depende da natureza e do tipo de interação entre os dois corpos durante a colisão..
Por sua vez, a velocidade relativa dos corpos antes da colisão definirá a intensidade da interação e, portanto, sua influência no coeficiente de restituição..
Como é calculado o coeficiente de restituição?
Para ilustrar como o coeficiente de restituição de uma colisão é calculado, tomaremos um caso simples:
Suponha que a colisão de duas esferas de massas M1 = 1 kg Y M2 = 2 kg movendo-se em um trilho reto sem atrito (como na figura 1).
A primeira esfera atinge com velocidade inicial V1 = 1 m / s no segundo que está originalmente em repouso, isto é V2 = 0 m / s.
Após a colisão, eles continuam se movendo assim: o primeiro para (V1 '= 0 m / s) e o segundo se move para a direita com velocidade V2 '= 1/2 m / s.
Para calcular o coeficiente de restituição nesta colisão, aplicamos a relação:
V1 ' - V2 ' = -e ( V1 - V2 )
0 m / s - 1/2 m / s = - e (1 m / s - 0 m / s) => - 1/2 = - e => e = 1/2 .
Exemplo
Na colisão unidimensional das duas esferas da seção anterior, seu coeficiente de restituição foi calculado, resultando em e = ½ .
Como e ≠ 1 a colisão não é elástica, ou seja, a energia cinética do sistema não é conservada e existe uma certa quantidade de energia dissipada Q (por exemplo, aquecimento das esferas devido à colisão).
Determine o valor da energia dissipada em Joules. Calcule também a porcentagem da fração de energia dissipada.
Solução
A energia cinética inicial da esfera 1 é:
K1i = ½ M1 V1 ^ 2 = ½ 1 kg (1 m / s) ^ 2 = ½ J
enquanto o da esfera 2 é zero porque está inicialmente em repouso.
Então, a energia cinética inicial do sistema é Ki = ½ J.
Após a colisão, apenas a segunda esfera se move com velocidade V2 '= ½ m / s, então a energia cinética final do sistema será:
Kf = ½ M2 V2 '^ 2 = ½ 2 kg (½ m / s) ^ 2 = ¼ J
Ou seja, a energia dissipada na colisão é:
Q = Ki - Kf = (½ J - ¼ J) = 1/4 J
E a fração de energia dissipada nesta colisão é calculada da seguinte forma:
f = Q / Ki = ¼ / ½ = 0,5 ou seja, 50% da energia do sistema foi dissipada devido à colisão inelástica cujo coeficiente de restituição é 0,5.
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill.
- Figueroa, D. 2005. Série: Física para Ciências e Engenharia. Volume 1. Cinemática. Editado por Douglas Figueroa (USB).
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1.
- Wikipedia. Quantidade de movimento recuperada de: en.wikipedia.org.



Ainda sem comentários