
Compressibilidade de sólidos, líquidos, gases, exemplos
O compressibilidade de uma substância ou material é a mudança de volume que ela experimenta quando é submetida a uma mudança na pressão. Em geral, o volume diminui quando a pressão é aplicada a um sistema ou objeto. No entanto, às vezes acontece o contrário: uma mudança na pressão pode produzir uma explosão na qual o sistema aumenta de volume ou quando ocorre uma mudança de fase..
Isso pode acontecer em algumas reações químicas e também nos gases, pois à medida que aumenta a frequência das colisões, ocorrem as forças repulsivas..

Ao imaginar como pode ser fácil ou difícil comprimir um objeto, considere os três estados em que a matéria normalmente se encontra: sólido, líquido e gasoso. Em cada um deles as moléculas mantêm certas distâncias umas das outras. Quanto mais fortes forem as ligações que unem as moléculas da substância que compõem o objeto e quanto mais próximas estiverem, mais difícil será causar uma deformação.
Um sólido tem suas moléculas muito próximas e, ao tentar aproximá-las, surgem forças repulsivas que dificultam a tarefa. Portanto, diz-se que os sólidos não são muito compressíveis. Nas moléculas de líquidos há mais espaço, logo sua compressibilidade é maior, mas mesmo assim a mudança de volume costuma exigir grandes forças.
Portanto, sólidos e líquidos dificilmente são compressíveis. Seria necessária uma variação de pressão muito grande para atingir uma alteração de volume apreciável sob as chamadas condições normais de pressão e temperatura. Por outro lado, os gases, como suas moléculas são amplamente espaçadas, são facilmente comprimidos e descomprimidos.
Índice do artigo
- 1 Compressibilidade de sólidos
- 1.1 - Compressibilidade de um material
- 2 exercícios-exemplos resolvidos
- 2.1 - Exercício resolvido 1
- 2.2 - Exercício resolvido 2
- 2.3 - Exercício resolvido 3
- 3 Compressibilidade em gases
- 3.1 - Exercício resolvido 5
- 4 referências
Compressibilidade sólida
Quando um objeto está imerso em um fluido, por exemplo, ele exerce pressão sobre o objeto em todas as direções. Desta forma, podemos pensar que o volume do objeto diminuirá, embora na maioria dos casos isso não seja apreciável..
A situação pode ser observada na figura a seguir:
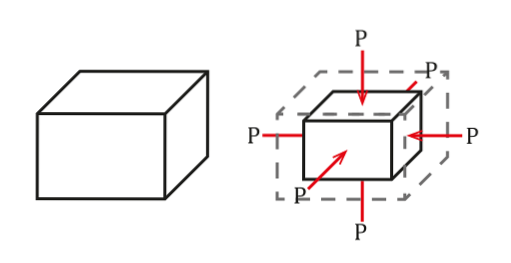
A pressão é definida como a força por unidade de área, que causará uma mudança de volume ΔV proporcional ao volume inicial do objeto Vou. Essa mudança de volume dependerá de suas qualidades..
A lei de Hooke afirma que a deformação experimentada por um objeto é proporcional à tensão aplicada a ele:
Tensão ∝ Tensão
A deformação volumétrica experimentada por um corpo é quantificada por B a constante de proporcionalidade exigida, que é chamada de módulo volumétrico do material:
B = -Stress / Strain
B = -ΔP / (ΔV / Vou)
Como ΔV / Vou é uma grandeza adimensional, por ser o quociente entre dois volumes, o módulo volumétrico possui as mesmas unidades de pressão, que no Sistema Internacional são Pascal (Pa).
O sinal negativo indica a redução esperada de volume, quando o objeto é comprimido o suficiente, ou seja, a pressão aumenta.
-Compressibilidade de um material
O valor inverso ou recíproco do módulo volumétrico é conhecido como compressibilidade e é denotado pela letra k. Portanto:

Aqui k é o negativo da mudança fracionária no volume por aumento na pressão. Suas unidades no Sistema Internacional são as inversas de Pa, ou seja, mdois / N.
A equação para B ou para k, se preferir, é aplicável a sólidos e líquidos. O conceito de módulo volumétrico raramente é aplicado a gases. Um modelo simples para quantificar a diminuição de volume que um gás real pode experimentar é explicado abaixo..
A velocidade do som e o módulo de compressibilidade
Uma aplicação interessante é a velocidade do som em um meio, que depende de seu módulo de compressibilidade:

Exemplos de exercícios resolvidos
-Exercício 1 resolvido
Uma esfera de latão maciço cujo volume é 0,8 m3 ele é jogado no oceano a uma profundidade onde a pressão hidrostática é 20 M Pa maior do que na superfície. Como o volume da esfera mudará? O módulo de compressibilidade do latão é conhecido por ser B = 35.000 MPa,
Solução
1 M Pa = 1 Mega pascal = 1,10 6 Pa
A variação de pressão em relação à superfície é DP = 20 x 10 6 Pa. Aplicando a equação dada para B, temos:
B = -ΔP / (ΔV / Vou)
Portanto:

ΔV = -5,71,10 -4 x 0,8 m3 = -4,57 x 10-4 m3
A diferença de volume pode ter um sinal negativo quando o volume final é menor que o volume inicial, portanto este resultado está de acordo com todas as suposições que fizemos até agora.
O módulo de compressibilidade muito alto indica que uma grande mudança na pressão é necessária para que o objeto experimente uma diminuição apreciável de volume..
-Exercício resolvido 2
Ao encostar o ouvido nos trilhos da ferrovia, você pode dizer quando um desses veículos está se aproximando ao longe. Quanto tempo leva o som ao viajar em um trilho de aço se o trem estiver a 1 km de distância?
Dados
Densidade do aço = 7,8 x 10 3 kg / m3
Módulo de compressibilidade do aço = 2,0 x 10 onze Pa.
Solução

O módulo de compressibilidade B calculado acima também se aplica a líquidos, embora um grande esforço seja geralmente necessário para produzir uma diminuição apreciável de volume. Mas os fluidos podem expandir ou contrair à medida que aquecem ou esfriam, e igualmente se forem despressurizados ou pressurizados..
Para água em condições padrão de pressão e temperatura (0 ° C e uma pressão atmosférica de aproximadamente ou 100 kPa), o módulo volumétrico é de 2100 MPa. Ou seja, cerca de 21.000 vezes a pressão atmosférica.
Por esse motivo, na maioria das aplicações, os líquidos são geralmente considerados incompressíveis. Isso pode ser verificado imediatamente com a aplicação numérica.
-Exercício resolvido 3
Encontre a diminuição fracionária do volume de água quando submetido a uma pressão de 15 MPa.
Solução

Compressibilidade em gases
Os gases, como explicado acima, funcionam um pouco diferente.
Para saber que volume eles têm n moles de um determinado gás quando mantido confinado a uma pressão P e a uma temperatura T, a equação de estado é usada. Na equação de estado de um gás ideal, onde as forças intermoleculares não são levadas em consideração, o modelo mais simples afirma que:
P.Videal = n. R. T
Onde R é a constante de gás ideal.
Mudanças no volume do gás podem ser realizadas a pressão ou temperatura constantes. Por exemplo, mantendo a temperatura constante, a compressibilidade isotérmica ΚT isso é:

Em vez do símbolo "delta" que foi usado antes na definição do conceito de sólidos, para um gás é descrito com uma derivada, neste caso derivada parcial em relação a P, mantendo T constante.
Portanto BT o módulo de compressibilidade isotérmica é:

E o módulo de compressibilidade adiabática B também é importante.adiabático, para o qual não há fluxo de calor de entrada ou saída.
Badiabático = γp
Onde γ é o coeficiente adiabático. Com este coeficiente, a velocidade do som no ar pode ser calculada:

Aplicando a equação acima, encontre a velocidade do som no ar.
Dados
O módulo de compressibilidade adiabática do ar é 1,42 × 105 Pa
A densidade do ar é de 1.225 kg / m3 (à pressão atmosférica e 15 ºC)
Solução

Em vez de trabalhar com o módulo de compressibilidade, como uma mudança de unidade no volume por mudança de pressão, o fator de compressibilidade de um gás real, um conceito diferente, mas ilustrativo de como o gás real se compara ao gás ideal:
P. Vreal = Z. R. T
Onde Z é o coeficiente de compressibilidade do gás, que depende das condições em que ele se encontra, sendo geralmente uma função tanto da pressão P quanto da temperatura T, e pode ser expresso como:
Z = f (P, T)
No caso de um gás ideal Z = 1. Para gases reais, o valor Z quase sempre aumenta com a pressão e diminui com a temperatura.
À medida que a pressão aumenta, as moléculas gasosas colidem com mais frequência e as forças repulsivas entre elas aumentam. Isso pode levar a um aumento no volume do gás real, em que Z> 1.
Em contraste, em pressões mais baixas, as moléculas são livres para se mover e as forças de atração predominam. Nesse caso, Z < 1.
Para o caso simples de 1 mol de gás n = 1, se as mesmas condições de pressão e temperatura forem mantidas, dividindo as equações anteriores termo por termo, obtemos:

Vreal = Z Videal
-Exercício resolvido 5
Existe um gás real a 250 ºK e 15 atm de pressão, que possui um volume molar 12% menor que o calculado pela equação de estado do gás ideal. Se a pressão e a temperatura forem mantidas constantes, encontre:
a) O fator de compressibilidade.
b) O volume molar do gás real.
c) Que tipo de forças predominam: atrativas ou repulsivas?
Solução
a) Se o volume real for 12% menor que o ideal, significa que:
Vreal = 0,88 Videal
Portanto, para 1 mol de gás, o fator de compressibilidade é:
Z = 0,88
b) Escolha da constante de gás ideal com as unidades adequadas para os dados fornecidos:
R = 0,082 L.atm / mol.K
O volume molar é calculado resolvendo e substituindo valores:
c) As forças atrativas predominam, uma vez que Z é menor que 1.
Referências
- Atkins, P. 2008. Physical Chemistry. Editorial Médica Panamericana. 10-15.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall. 242-243 e 314-15
- Mott, R. 2006. Mecânica dos fluidos. Pearson Education 13-14.
- Rex, A. 2011. Fundamentals of Physics. Pearson Education. 242-243.
- Tipler, P. (2006) Physics for Science and Technology. 5ª Ed. Volume 1. Editorial Reverté. 542.

Ainda sem comentários