O condutância de um condutor é definido como a facilidade que ele tem para passar a corrente elétrica. Depende não só do material utilizado para sua fabricação, mas também de sua geometria: comprimento e área da seção transversal.
O símbolo usado para condutância é G, e é o inverso da resistência elétrica R, uma quantidade um pouco mais familiar. A unidade SI International System para condutância é o inverso do ohm, denotado como Ω-1 e recebe o nome de siemens (S).
Outros termos usados em eletricidade que soam semelhantes à condutância e estão relacionados são condutividade e a dirigindo, mas eles não devem ser confundidos. O primeiro desses termos é uma propriedade intrínseca da substância com a qual o condutor é feito e o segundo descreve o fluxo de carga elétrica através dele..
Para um condutor elétrico com área transversal constante PARA, comprimento eu e condutividade σ, a condutância é dada por:
G = σ.A / L
Quanto maior a condutividade, maior a condutância. Além disso, quanto maior for a área da seção transversal, mais fácil será para o condutor passar a corrente. Ao contrário, quanto maior o comprimento L, menor a condutância, uma vez que os portadores de corrente perdem mais energia em caminhos mais longos..
Índice do artigo
A condutância G para um condutor com área de seção transversal constante é calculada de acordo com a equação dada acima. Isso é importante, porque se a seção transversal não for constante, você deve usar o cálculo integral para encontrar a resistência e a condutância.
Por ser o inverso da resistência, a condutância G pode ser calculada sabendo que:
G = 1 / R
Na verdade, a resistência elétrica de um condutor pode ser medida diretamente com um multímetro, um dispositivo que também mede corrente e tensão..
Conforme afirmado no início, a unidade de condutância no sistema internacional é a Siemens (S). Diz-se que um condutor tem uma condutância de 1 S se a corrente através dele aumentar em 1 ampere para cada volt de diferença de potencial.
Vamos ver como isso é possível através da lei de Ohm, se for escrita em termos de condutância:
V = I.R = I / G
Onde V é a diferença de tensão ou potencial entre as extremidades do condutor e eu intensidade atual. Em termos dessas magnitudes, a fórmula se parece com esta:
G = I / V
Anteriormente, a unidade de condutância era o mho (ohm escrito ao contrário) denotado como Ʊ, que é um ômega capital invertido. Esta notação foi descontinuada e foi substituída pelo siemens em homenagem ao engenheiro e inventor alemão Ernst Von Siemens (1816-1892), pioneiro das telecomunicações, mas ambos são totalmente equivalentes.
1 mho = 1 siemens = 1 A / V (ampere / volt)
Em outros sistemas de medição, o statsiemens (statS) (no sistema cgs ou centímetro-grama-segundo) e o absiemens (abS) (sistema cgs eletromagnético) com o "s" no final, sem indicar singular ou plural, pois provêm de um nome próprio.
Algumas equivalências
1 statS = 1,11265 x 10 -12 siemens
1 abS = 1 x 109 siemens
Como mencionado antes, tendo a resistência, a condutância é imediatamente conhecida na determinação do valor inverso ou recíproco. Desta forma, uma resistência elétrica de 100 ohm é equivalente a 0,01 siemens, por exemplo.
Aqui estão mais dois exemplos do uso de condutância:
São termos diferentes, conforme já indicado. A condutividade é uma propriedade da substância com a qual o condutor é feito, enquanto a condutância é própria do condutor.
A condutividade pode ser expressa em termos de G como:
σ = G. (L / A)
Aqui está uma tabela com as condutividades de materiais condutores usados com frequência:
tabela 1. Condutividades, resistividades e coeficientes térmicos de alguns condutores. Temperatura de referência: 20 ºC.
| Metal | σ x 106 (Vós) | ρ x 10-8 (Ω.m) | α ºC-1 |
|---|---|---|---|
| Prata | 62,9 | 1,59 | 0,0058 |
| Cobre | 56,5 | 1,77 | 0,0038 |
| Ouro | 41,0 | 2,44 | 0,0034 |
| Alumínio | 35,4 | 2,82 | 0,0039 |
| Tungstênio | 18,0 | 5,60 | 0,0045 |
| Ferro | 10,0 | 10,0 | 0,0050 |
Quando você tem circuitos com resistores em paralelo, às vezes é necessário obter a resistência equivalente. Saber o valor da resistência equivalente permite substituir um único valor pelo conjunto de resistores.
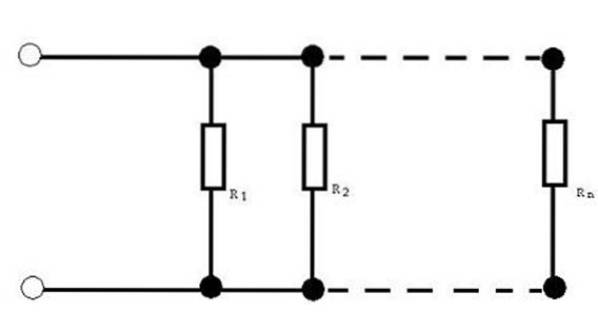
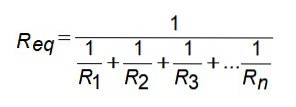
Para esta configuração de resistor, a resistência equivalente é dada por:
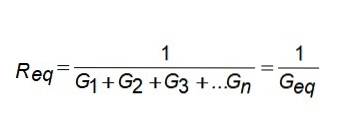
Geq = G1 + Gdois + G3 +… Gn
Ou seja, a condutância equivalente é a soma das condutâncias. Se você quiser saber a resistência equivalente, basta inverter o resultado.
a) Escreva a lei de Ohm em termos de condutância.
b) Encontre a condutância de um fio de tungstênio de 5,4 cm de comprimento e 0,15 mm de diâmetro.
c) Agora, uma corrente de 1,5 A passa pelo fio. Qual é a diferença de potencial entre as pontas deste condutor?
Nas seções anteriores, você deve:
V = I / G
G = σ.A / L
Substituindo o último no primeiro, fica assim:
V = I /(σ.A/L) = I.L / σ.A
Onde:
-Eu é a intensidade da corrente.
-L é o comprimento do condutor.
-σ é a condutividade.
-A é a área da seção transversal.
Para calcular a condutância deste fio de tungstênio, sua condutividade é necessária, que se encontra na Tabela 1:
σ = 18 x106 vós
L = 5,4 cm = 5,4 x 10-dois m
D = 0,15 mm = 0,15 x 10-3 m
A = π.Ddois / 4 = π. (0,15 x 10-3 m)dois / 4 = 1,77 x 10-8 mdois
Substituindo na equação, temos:
G = σ.A / L = 18 x 106 Vós . 1,77 x 10-8 mdois / 0,15 x 10-3 m = 2120,6 S.
V = I / G = 1,5 A / 2120,6 S = 0,71 mV.
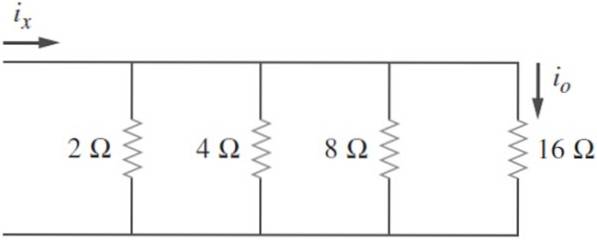
Encontre a resistência equivalente no seguinte circuito e sabendo que iou = 2 A, calcule ix e a potência dissipada pelo circuito:
Os resistores são listados: R1= 2 Ω; Rdois= 4 Ω; R3= 8 Ω; R4= 16 Ω
Em seguida, a condutância é calculada em cada caso: G1 = 0,5 Ʊ; Gdois = 0,25 Ʊ; G3 = 0,125 Ʊ; G4 = 0,0625 Ʊ
E, finalmente, eles são adicionados conforme indicado antes, para encontrar a condutância equivalente:
Geq = G1 + Gdois + G3 +… Gn = 0,5 Ʊ + 0,25 Ʊ + 0,125 Ʊ + 0,0625 Ʊ = 0,9375 Ʊ
Portanto Req = 1,07 Ω.
A tensão em R4 é v4 = iou. R4 = 2 A. 16 Ω = 32 V, e é igual para todos os resistores, já que estão conectados em paralelo. Então é possível encontrar as correntes que fluem através de cada resistência:
-eu1 = V1 / R1 = 32 V / 2 Ω = 16 A
-eudois = Vdois / Rdois = 32 V / 4 Ω = 8 A
-eu3 = V3 / R3 = 32 V / 8 Ω = 4 A
-eux = i1 + eudois + eu3 + euou = 16 + 8 + 4 + 2 A = 30 A
Finalmente, a potência dissipada P é:
P = (ix)dois. Req = 30 A x 1,07 Ω = 32,1 W
Ainda sem comentários