
Congruência figuras congruentes, critérios, exemplos, exercícios
O congruência, Na geometria, indica que, se duas figuras planas têm a mesma forma e dimensões, são congruentes. Por exemplo, dois segmentos são congruentes quando seus comprimentos são iguais. Da mesma forma, ângulos congruentes têm a mesma medida, embora não sejam orientados da mesma maneira no plano..
O termo "congruência" vem do latim congruente, cujo significado é correspondência. Assim, duas figuras congruentes correspondem exatamente uma à outra..
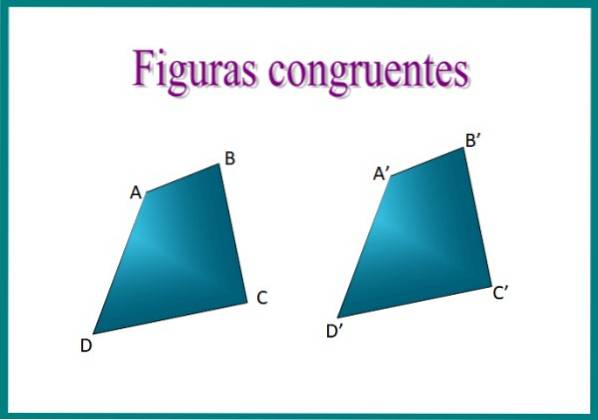
Por exemplo, se sobrepormos os dois quadriláteros na imagem, descobriremos que eles são congruentes, uma vez que a disposição de seus lados é idêntica e medem o mesmo.
Colocando os quadriláteros ABCD e A'B'C'D 'um em cima do outro, os números corresponderão exatamente. Os lados correspondentes são chamados lados homólogos ou correspondente e para expressar congruência o símbolo ≡ é usado. Então podemos afirmar que ABCD ≡ A'B'C'D '.
Índice do artigo
- 1 critério de congruência
- 1.1 Congruência, identidade e semelhança
- 2 exemplos de congruência
- 2.1 - Congruência angular
- 2.2 - Congruência de triângulos
- 3 exercícios resolvidos
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 4 referências
Critérios de congruência
As seguintes características são comuns a polígonos congruentes:
-Mesmo formato e tamanho.
-Medidas idênticas de seus ângulos.
-A mesma medida em cada um de seus lados.
No caso de dois polígonos em questão serem regulares, ou seja, todos os lados e ângulos internos medem o mesmo, a congruência é assegurada quando é cumprida algum das seguintes condições:
-Os lados são congruentes
-As apotemas eles têm a mesma medida
-O rádio de cada polígono mede igual
O apótema de um polígono regular é a distância entre o centro e um dos lados, enquanto o raio corresponde à distância entre o centro e um vértice ou canto da figura.
Os critérios de congruência são freqüentemente usados porque muitas partes e peças de todos os tipos são produzidas em massa e devem ter a mesma forma e medidas. Desta forma, eles podem ser facilmente substituídos quando necessário, por exemplo, porcas, parafusos, folhas ou lajes no chão da rua..

Congruência, identidade e semelhança
Existem conceitos geométricos relacionados à congruência, por exemplo figuras idênticas e as figuras semelhantes, isso não implica necessariamente que os números sejam congruentes.
Observe que as figuras congruentes são idênticas, porém os quadriláteros na Figura 1 podem ser orientados de maneiras diferentes no plano e ainda assim permanecer congruentes, uma vez que a orientação diferente não altera o tamanho de seus lados ou seus ângulos. Neste caso, eles deixariam de ser idênticos.
O outro conceito é o da semelhança de figuras: duas figuras planas são semelhantes se têm a mesma forma e seus ângulos internos medem o mesmo, embora o tamanho das figuras possa ser diferente. Se for esse o caso, os números não são congruentes.
Exemplos de congruência
- Congruência angular
Como indicamos no início, ângulos congruentes têm a mesma medida. Existem várias maneiras de obter ângulos congruentes:
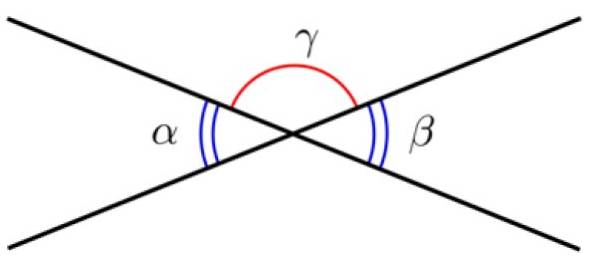
Exemplo 1
Duas linhas com um ponto em comum definem dois ângulos, chamados Ângulos opostos pelo vértice. Esses ângulos têm a mesma medida, portanto são congruentes.
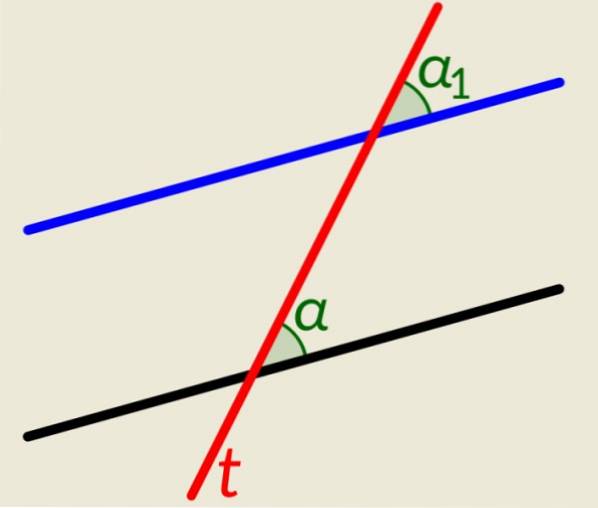
Exemplo 2
Existem duas linhas paralelas mais uma linha t que cruza os dois. Como no exemplo anterior, quando esta linha cruza os paralelos, ela gera ângulos congruentes, um em cada linha do lado direito e outros dois do lado esquerdo. A figura mostra α e α1, à direita da linha t, que são congruentes.
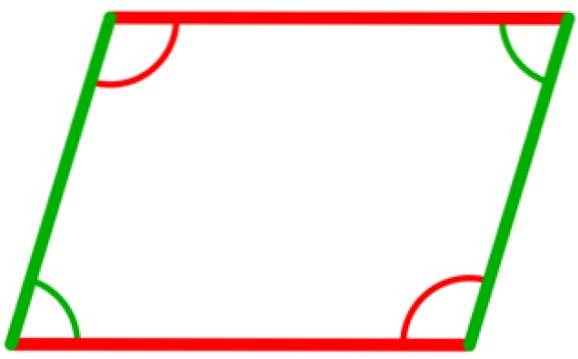
Exemplo 3
Em um paralelogramo, existem quatro ângulos internos, que são congruentes de dois para dois. São aqueles que se encontram entre vértices opostos, como mostra a figura a seguir, em que os dois ângulos em verde são congruentes, assim como os dois ângulos em vermelho.
- Congruência de triângulos
Dois triângulos da mesma forma e tamanho são congruentes. Para verificar isso, existem três critérios que podem ser examinados em busca de congruência:
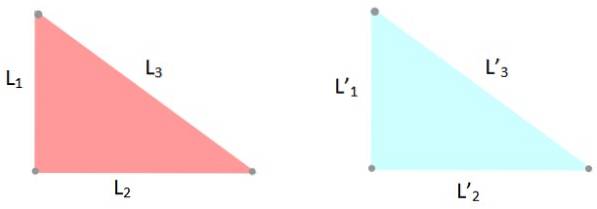
-Critério LLL: os três lados dos triângulos têm as mesmas medidas, portanto L1 = L '1; eudois = L 'dois e eu3 = L '3.
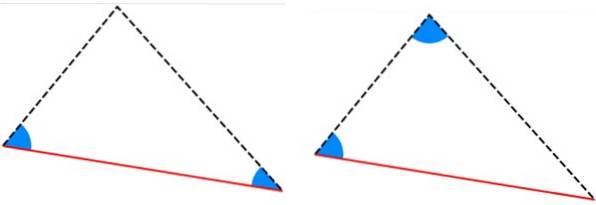
-Critérios ALA e AAL: triângulos têm dois ângulos internos iguais e o lado entre esses ângulos tem a mesma medida.
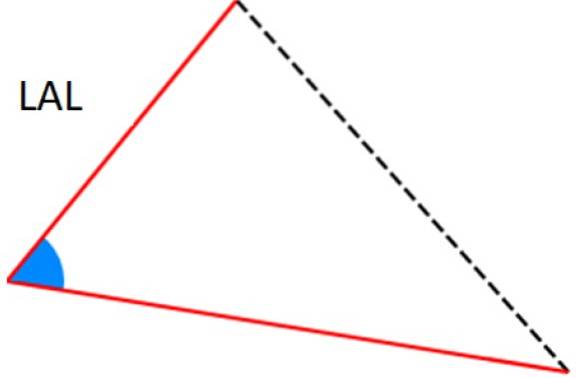
-Critério LAL: dois dos lados são idênticos (correspondentes) e entre eles há o mesmo ângulo.
Exercícios resolvidos
- Exercício 1
Dois triângulos são mostrados na figura a seguir: ΔABC e ΔECF. Sabe-se que AC = EF, que AB = 6 e que CF = 10. Além disso, os ângulos ∡BAC e ∡FEC são congruentes e os ângulos ∡ACB e ∡FCB também são congruentes..
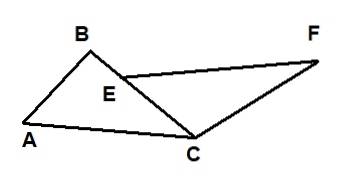
Então, o comprimento do segmento BE é igual a:
(i) 5
(ii) 3
(iii) 4
(iv) 2
(v) 6
Solução
Como os dois triângulos têm um lado de igual comprimento AC = EF compreendido entre os ângulos iguais ∡BAC = ∡CEF e ∡BCA = ∡CFE, pode-se dizer que os dois triângulos são congruentes pelo critério ALA.
Ou seja, ΔBAC ≡ ΔCEF, então temos que:
BA = CE = AB = 6
BC = CF = 10
AC = EF
Mas o segmento a ser calculado é BE = BC - EC = 10 - 6 = 4.
Portanto, a resposta correta é (iii).
- Exercício 2
Três triângulos são mostrados na figura abaixo. Sabe-se também que os dois ângulos indicados medem 80º cada e que os segmentos AB = PD e AP = CD. Encontre o valor do ângulo X indicado na figura.
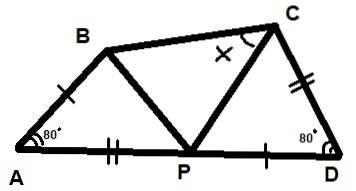
Solução
Você tem que aplicar as propriedades dos triângulos, que são detalhadas passo a passo.
Passo 1
Começando com o critério de congruência do triângulo LAL, pode-se afirmar que os triângulos BAP e PDC são congruentes:
ΔBAP ≡ ΔPDC
Passo 2
O exposto acima leva a afirmar que BP = PC, portanto o triângulo ΔBPC é isósceles e ∡PCB = ∡PBC = X.
etapa 3
Se chamarmos o ângulo de BPC γ, segue-se que:
2x + γ = 180º
Passo 4
E se chamarmos os ângulos APB e DCP de β e α os ângulos ABP e DPC, temos:
α + β + γ = 180º (uma vez que APB é um ângulo plano).
Etapa 5
Além disso, α + β + 80º = 180º pela soma dos ângulos internos do triângulo APB.
Etapa 6
Combinando todas essas expressões, temos:
α + β = 100º
Etapa 7
E, por conseguinte:
γ = 80º.
Etapa 8
Finalmente, segue-se que:
2X + 80º = 180º
Com X = 50º.
Referências
- Baldor, A. 1973. Plane and Space Geometry. Cultural da América Central.
- Fundação CK-12. Polígonos congruentes. Recuperado de: ck 12.org.
- Desfrute de matemática. Definições: Raio (polígono). Recuperado de: gustolasmatematicas.com.
- Referência de matemática aberta. Testando polígonos para congruência. Recuperado de: mathopenref.com.
- Wikipedia. Congruência (geometria). Recuperado de: es.wikipedia.org.
- Zapata, F. Triângulos, história, elementos, classificação, propriedades. Recuperado de: lifeder.com.



Ainda sem comentários