
Propriedades de conjuntos finitos, exemplos, exercícios resolvidos
É compreendido por conjunto finito qualquer conjunto com um número limitado ou contável de elementos. Exemplos de conjuntos finitos são as bolas de gude que estão contidas em uma bolsa, o conjunto de casas em um bairro ou o conjunto P formado pelos primeiros vinte (20) números naturais:
P = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
O conjunto de estrelas no universo é certamente imenso, mas não se sabe ao certo se é finito ou infinito. No entanto, o conjunto de planetas do sistema solar é finito.
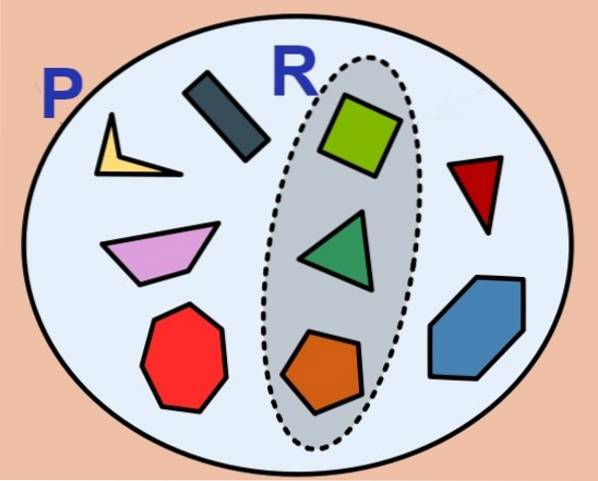
O número de elementos de um conjunto finito é chamado de cardinalidade e para o conjunto P é denotado assim: Cartão (P) ou #P. O conjunto vazio tem cardinalidade zero e é considerado um conjunto finito.
Índice do artigo
- 1 propriedades
- 2 exemplos
- 2.1 Mais exemplos
- 3 exercícios resolvidos
- 3.1 Exercício 1
- 3.2 Exercício 2
- 3.3 Exercício 3
- 3.4 Exercício 4
- 4 referências
Propriedades
Entre as propriedades dos conjuntos finitos estão as seguintes:
1- A união de conjuntos finitos dá origem a um novo conjunto finito.
2- Se dois conjuntos finitos se cruzam, um novo conjunto finito resulta.
3- Um subconjunto de um conjunto finito é finito e sua cardinalidade é menor ou igual à do conjunto original.
4- O conjunto vazio é um conjunto finito.
Exemplos
Existem muitos exemplos de conjuntos finitos. Alguns exemplos incluem o seguinte:
O conjunto M dos meses do ano, que de forma ampliada pode ser escrita assim:
M = Janeiro, fevereiro, março, abril, maio, junho, julho, agosto, setembro, outubro, novembro, dezembro, a cardinalidade de M é 12.
O conjunto S dos dias da semana: S = Segunda, Terça, Quarta, Quinta, Sexta, Sábado, Domingo. A cardinalidade de S é 7.
O conjunto Ñ das letras do alfabeto espanhol é um conjunto finito, este conjunto por extensão é escrito assim:
Ñ = a, b, c, d, e, f, g, h, i, j, k, l, m, n, ñ, o, p, q, r, s, t, u, v, w, x, y, z e sua cardinalidade é 27.
O conjunto V das vogais em espanhol é um subconjunto do conjunto Ñ:
V ⊂ Ñ portanto, é um conjunto finito.
O conjunto finito V em forma extensa, é escrito assim: V = a, e, i, o, u e sua cardinalidade é 5.
Os conjuntos podem ser expressos por compreensão. O conjunto F composto pelas letras da palavra "finito" é um exemplo:
F = x / x é uma letra da palavra "finito"
O referido conjunto expresso de forma extensiva será:
F = f, i, n, t, o cuja cardinalidade é 5 e, portanto, é um conjunto finito.
Mais exemplos
As cores do arco-íris são outro exemplo de um conjunto finito, o conjunto C dessas cores é:
C = vermelho, laranja, amarelo, verde, ciano, azul, violeta e sua cardinalidade é 7.
O conjunto de fases F de la Luna é outro exemplo de um conjunto finito:
F = Lua nova, primeiro quarto, lua cheia, quarto minguante este conjunto tem cardinalidade 4.
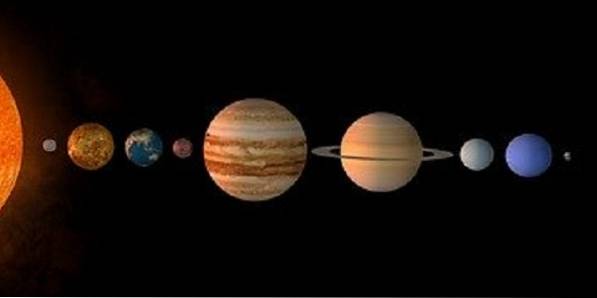
Outro conjunto finito é aquele formado pelos planetas do sistema solar:
P = Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano, Netuno, Plutão de cardinalidade 9.
Exercícios resolvidos
Exercício 1
O seguinte conjunto A = x∊ R / x ^ 3 = 27 é dado. Expresse em palavras e escreva por extensão, indique sua cardinalidade e diga se é finito ou não.
Solução: O conjunto A é o conjunto de números reais x tais que x ao cubo de como resultado 27.
A equação x ^ 3 = 27 tem três soluções: são x1 = 3, x2 = (-3/2 + 3√3 / 2 i) e x3 = (-3/2 - 3√3 / 2 i). Das três soluções, apenas x1 é real, enquanto as outras duas são números complexos.
Uma vez que a definição do conjunto A diz que x pertence aos números reais, então as soluções nos números complexos não fazem parte do conjunto A.
O conjunto A expresso extensivamente é:
A = 3, que é um conjunto finito de cardinalidade 1.
Exercício 2
Escreva de forma simbólica (por compreensão) e de forma extensiva o conjunto B de números reais maiores que 0 (zero) e menores ou iguais a 0 (zero). Indique sua cardinalidade e se é finito ou não.
Solução: B = x∊ R / 0 < x <= 0
O conjunto B está vazio porque um número real x não pode ser simultaneamente maior e menor que zero, assim como não pode ser 0 e também menor que 0.
B = e sua cardinalidade é 0. O conjunto vazio é um conjunto finito.
Exercício 3
O conjunto S das soluções de uma certa equação é dado. O conjunto S por compreensão é escrito assim:
S = x∊ R / (x-3) (x ^ 2 - 9x + 20) = 0
Escreva o referido conjunto de forma extensa, indique a sua cardinalidade e indique se é ou não um conjunto finito.
Solução: Em primeiro lugar, ao analisar a expressão que descreve o conjunto S, obtém-se que se trata de um conjunto de valores de x reais que são soluções da equação:
(x-3) (x ^ 2 - 9x + 20) = 0 (*)
Uma solução dessa equação é x = 3, que é um número real e, portanto, pertence a S. Mas há mais soluções que podem ser obtidas procurando as soluções da equação quadrática:
(x ^ 2 - 9x + 20) = 0
A expressão acima pode ser fatorada da seguinte maneira:
(x - 4) (x - 5) = 0
O que nos leva a mais duas soluções da equação original (*) que são x = 4 ex = 5. Em suma, a equação (*) tem como soluções 3, 4 e 5.
O conjunto S expresso de forma extensa tem a seguinte aparência:
S = 3, 4, 5, que tem cardinalidade 3 e, portanto, é um conjunto finito.
Exercício 4
Existem dois conjuntos A = 1, 5, 7, 9, 11 e B = x ∊ N / x é par ^ x < 10 .
Escreva explicitamente o conjunto B e encontre a união com o conjunto A. Encontre também a interceptação desses dois conjuntos e conclua.
Solução: o conjunto B é composto de números naturais, de modo que eles são pares e também menores do que o valor 10, portanto, no conjunto B na forma extensa é escrito da seguinte forma:
B = 2, 4, 6, 8
A união do conjunto A com o conjunto B é:
A U B = 1, 2, 4, 5, 6, 7, 8, 9, 11
e a interceptação do conjunto A com o conjunto B é escrita assim:
A ⋂ B = = Ø é o conjunto vazio.
Deve-se notar que a união e interceptação desses dois conjuntos finitos levam a novos conjuntos, que por sua vez também são finitos.
Referências
- Fuentes, A. (2016). MATEMÁTICA BÁSICA. Uma introdução ao cálculo. Lulu.com.
- Garo, M. (2014). Matemática: equações quadráticas: Como resolver uma equação quadrática. Marilù Garo.
- Haeussler, E. F., & Paul, R. S. (2003). Matemática para gestão e economia. Pearson Education.
- Jiménez, J., Rodríguez, M., Estrada, R. (2005). Matemática 1 SEP. Limiar.
- Preciado, C. T. (2005). Curso de Matemática 3º. Progreso Editorial.
- Matemática 10 (2018). "Exemplos de conjuntos finitos". Recuperado de: matematicas10.net
- Rock, N. M. (2006). Álgebra I é fácil! Tão fácil. Team Rock Press.
- Sullivan, J. (2006). Álgebra e trigonometria. Pearson Education.
- Wikipedia. Conjunto finito. Recuperado de: es.wikipedia.com


Ainda sem comentários