
História constante de Boltzmann, equações, cálculo, exercícios
O Constante de Boltzmann é o valor que relaciona a energia cinética média de um sistema termodinâmico ou de um objeto com sua temperatura absoluta. Embora sejam frequentemente confundidos, temperatura e energia não são o mesmo conceito.
A temperatura é uma medida de energia, mas não a energia em si. Com a constante de Boltzmann, eles estão ligados entre si da seguinte forma:
Ec = (3/2) kB T

Esta equação é válida para uma molécula de gás monatômica ideal de massa m, Onde Ec é a sua energia cinética dada em Joules, kB é a constante de Boltzmann e T é a temperatura absoluta em Kelvin.
Dessa forma, quando a temperatura aumenta, a energia cinética média por molécula de substância também aumenta, como é esperado. E o contrário acontece quando a temperatura diminui, podendo chegar ao ponto em que, se todo o movimento cessa, atinge-se a temperatura mais baixa possível ou o zero absoluto..
Ao falar sobre a energia cinética média, é necessário lembrar que a energia cinética está associada ao movimento. E as partículas podem se mover de várias maneiras, como mover-se, girar ou vibrar. É claro que nem todos o farão da mesma forma e, como são incontáveis, a média é tomada para caracterizar o sistema..
Alguns estados de energia são mais prováveis do que outros. Este conceito é de importância radical na termodinâmica. A energia considerada na equação acima é a energia cinética translacional. A probabilidade dos estados e sua relação com a constante de Boltzmann serão discutidas um pouco mais tarde..
Em 2018 o Kelvin foi redefinido e com ele a constante de Boltzmann, que no Sistema Internacional é de aproximadamente 1,380649 x 10-2,3 J. K-1. Muito mais precisão pode ser alcançada para a constante de Boltzmann, que foi determinada em vários laboratórios ao redor do mundo, por diferentes métodos..
Índice do artigo
- 1 história
- 1.1 Constante de Boltzmann e obras de Planck
- 2 Valor e equações
- 3 Constante e entropia de Boltzmann
- 4 Como o kB é calculado?
- 5 exercícios resolvidos
- 5.1 - Exercício 1
- 6 referências
História
A famosa constante deve seu nome ao físico vienense Ludwig Boltzmann (1844-1906), que dedicou sua vida como cientista ao estudo do comportamento estatístico de sistemas com muitas partículas, do ponto de vista da mecânica newtoniana..
Embora hoje a existência do átomo seja universalmente aceita, no século XIX a crença sobre se o átomo realmente existia ou se era um artifício com o qual muitos fenômenos físicos eram explicados estava em pleno debate..
Boltzmann foi um ferrenho defensor da existência do átomo e, em sua época, enfrentou duras críticas de muitos colegas a seu trabalho, que consideravam que continha paradoxos insolúveis..
Ele afirmou que fenômenos observáveis em níveis macroscópicos podem ser explicados pelas propriedades estatísticas das partículas constituintes, como átomos e moléculas..
Talvez essas críticas se devam ao profundo episódio de depressão que o levou a se suicidar no início de setembro de 1906, quando ainda tinha muito que fazer, pois foi considerado um dos grandes físicos teóricos de sua época e houve muito pouco resta para ir. que outros cientistas contribuem para corroborar a veracidade de suas teorias.
Não muito depois de sua morte, novas descobertas sobre a natureza do átomo e suas partículas constituintes se somaram para provar que Boltzmann estava certo..
Constante de Boltzmann e obras de Planck
Agora, a constante de Boltzmann kB foi introduzido como é conhecido hoje, algum tempo depois dos trabalhos do físico austríaco. Foi Max Planck, na sua lei da emissão do corpo negro, obra que apresentou em 1901, que então lhe atribuiu o valor de 1,34 x 10-23 J / K.
Por volta de 1933, uma placa com a definição de entropia envolvendo a famosa constante foi adicionada à lápide de Boltzmann em Viena como uma homenagem póstuma: S = kB log W, equação que será discutida mais tarde.
Hoje, a constante de Boltzmann é indispensável na aplicação das leis da termodinâmica, da mecânica estatística e da teoria da informação, campos dos quais esse físico com final triste foi um dos pioneiros..
Valor e equações
Os gases podem ser descritos em termos macroscópicos e também em termos microscópicos. Para a primeira descrição existem conceitos como densidade, temperatura e pressão.
No entanto, deve-se lembrar que um gás é composto de muitas partículas, que apresentam tendência global para determinado comportamento. É essa tendência que é medida macroscopicamente. Uma maneira de determinar a constante de Boltzmann é graças à conhecida equação do gás ideal:
p.V = n. R. T
Aqui p é a pressão do gás, V é o seu volume, n é o número de moles presentes, R é a constante do gás e T é a temperatura. Em um mol de gás ideal, a seguinte relação é cumprida entre o produto p.V, e a energia cinética translacional K todo o conjunto é:
p.V = (2/3). K
Portanto, a energia cinética é:
K = (3/2) n.R.T
Dividindo pelo número total de moléculas presentes, que será denominado N, obtém-se a energia cinética média de uma única partícula:
Ec = K / N
Ec= (3 / 2N) n.R.T
Em um mol está o número de partículas N de AvogadroPARA, e, portanto, o número total de partículas é N = nNA, restante:
Ec = (3 / 2nNPARA) n.R.T
Precisamente o quociente R / NPARA é a constante de Boltzmann, sendo assim mostrado que a energia cinética translacional média de uma partícula depende apenas da temperatura absoluta T e não de outras grandezas como pressão, volume ou mesmo o tipo de molécula:
Ec = (3/2) kB. T
Constante e entropia de Boltzmann
Um gás tem uma determinada temperatura, mas essa temperatura pode corresponder a diferentes estados de energia interna. Como visualizar essa diferença?
Considere o lançamento simultâneo de 4 moedas e as maneiras pelas quais elas podem cair:
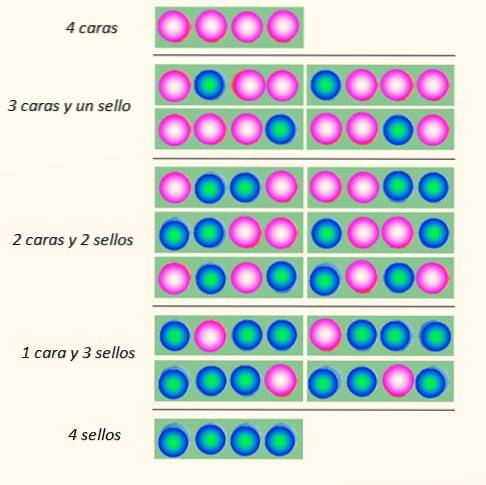
O conjunto de moedas pode assumir um total de 5 estados, que são considerados macroscópico, descrito na figura. Qual desses estados o leitor diria que é o mais provável?
A resposta deve ser o estado de 2 caras e 2 coroas, pois você tem um total de 6 possibilidades, das 16 ilustradas na figura. E 24 = 16. Estes são equivalentes aos estados microscópico.
E se 20 moedas forem lançadas em vez de 4? Haveria um total de 2vinte possibilidades ou "estados microscópicos". É um número muito maior e mais difícil de manusear. Para facilitar o manuseio de grandes números, os logaritmos são muito apropriados.
Agora, o que parece evidente é que o estado com maior desordem é o mais provável. Estados mais ordenados como 4 cabeças ou 4 selos são ligeiramente menos prováveis.
A entropia de um estado macroscópico S é definida como:
S = kB ln w
Onde C é o número de possíveis estados microscópicos do sistema e kB é a constante de Boltzmann. o que ln w é adimensional, a entropia tem as mesmas unidades que kB: Joule / K.
Esta é a famosa equação da lápide de Boltzmann em Viena. Porém, mais do que entropia, o que importa é sua mudança:
ΔS = kB ln wdois - kB ln w1 = kB ln (wdois/ C1)
Como você calcula kB?
O valor da constante de Boltzmann é obtido experimentalmente com extrema precisão com medições baseadas em termometria acústica, que são realizadas usando a propriedade que estabelece a dependência da velocidade do som em um gás com sua temperatura.
Na verdade, a velocidade do som em um gás é dada por:

Badiabático = γp
E ρ é a densidade do gás. Para a equação acima, p é a pressão do gás em questão e γ é o coeficiente adiabático, cujo valor para um determinado gás é encontrado nas tabelas.
Os institutos de metrologia também estão experimentando outras formas de medir a constante, como o Johnson Noise Thermometry, que usa flutuações térmicas que ocorrem aleatoriamente em materiais, principalmente condutores.
Exercícios resolvidos
-Exercício 1
Achar:
a) Energia cinética translacional média Ec que tem uma molécula de gás ideal a 25 ºC
b) Energia cinética translacional K das moléculas em 1 mol deste gás
c) A velocidade média de uma molécula de oxigênio a 25 ºC
Facto
moxigênio = 16 x 10 -3 kg / mol
Solução
para) Ec = (3/2) k T = 1,5 x 1,380649 x 10-2,3J. K-1 x 298 K = 6,2 x 10-vinte e um J
b) K = (3/2) n.R.T = 5 x 1 mol x 8,314 J / mol. K x 298 K = 3716 J
c) Ec = ½ mvdois, levando em consideração que a molécula de oxigênio é diatômica e a massa molar deve ser multiplicada por 2, teremos:

Encontre a mudança na entropia quando 1 mol de gás ocupando um volume de 0,5 m3 se expande para ocupar 1 m3.
Solução
ΔS = kB ln (wdois/ C1)
Cdois= 2NC1 (Havia 24 estados microscópicos para o lançamento das 4 moedas, lembra?)
Onde N é o número de partículas presentes em 0,5 mol de gás 0,5 x NPARA:
ΔS = kB ln (2N C1/ C1) = kB em 2N= kB 0,5NPARA ln 2 = 2,88 J / K
Referências
- Atkins, P. 1999. Physical Chemistry. Edições Omega. 13-47.
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill. 664-672.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º… Ed Prentice Hall. 443 -444.
- Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1. 647-673.
- SIM Redefinição. Kelvin: Boltzmann Constant. Obtido em: nist.gov

Ainda sem comentários