
Constante de proporcionalidade o que é, cálculo, exercícios
O constante de proporcionalidade É um elemento numérico relacional, usado para definir o padrão de similaridade entre 2 grandezas que são alteradas simultaneamente. É muito comum representá-lo como uma função linear de forma genérica usando a expressão F (X) = k.X. No entanto, esta não é a única representação de uma possível proporcionalidade.
Por exemplo, a relação entre X e Y na função Y = 3x possui uma constante de proporcionalidade igual a 3. Observa-se que à medida que a variável independente X cresce, também cresce a variável dependente Y, pelo triplo de seu valor anterior.
As alterações aplicadas a uma variável repercutem imediatamente na outra, de modo que há um valor conhecido como constante de proporcionalidade. Isso serve para relacionar as diferentes magnitudes que ambas as variáveis adquirem.
Índice do artigo
- 1 Qual é a constante de proporcionalidade e tipos
- 1.1 Proporcionalidade direta
- 1.2 Proporcionalidade inversa ou indireta
- 2 Como é calculado?
- 2.1 De acordo com seu gráfico
- 2.2 De acordo com a tabela de valores
- 2.3 De acordo com a expressão analítica
- 2.4 Por regra direta ou composta de três
- 3 História
- 4 exercícios resolvidos
- 4.1 Exercício 1
- 4.2 Exercício 2
- 5 referências
Qual é a constante de proporcionalidade e tipos
De acordo com a tendência na mudança das variáveis, as proporcionalidades podem ser classificadas em 2 tipos.
Proporcionalidade direta
Sugere uma relação unilateral entre duas quantidades. Nele, se a variável independente apresentar algum crescimento, a variável dependente também crescerá. Da mesma forma, qualquer diminuição na variável independente causará uma diminuição na magnitude de Y.
Por exemplo, a função linear usada na introdução; Y = 3X, corresponde a uma relação direta de proporcionalidade. Isso ocorre porque o aumento na variável independente X causará um aumento triplo no valor anterior tomado pela variável dependente Y.
Da mesma forma, a variável dependente diminuirá três vezes seu valor quando X diminuir em magnitude.
O valor da constante de proporcionalidade "K" em uma relação direta é definido como K = Y / X.
Proporcionalidade inversa ou indireta
Neste tipo de funções, a relação entre as variáveis é apresentada de forma antínima, onde o crescimento ou diminuição da variável independente corresponde respectivamente à diminuição ou crescimento da variável dependente..
Por exemplo, a função F (x) = k / x é uma relação inversa ou indireta. Uma vez que o valor da variável independente começa a aumentar, o valor de k será dividido por um número crescente, fazendo com que a variável dependente diminua de valor de acordo com a proporção.
Dependendo do valor obtido por K, a tendência da função proporcional inversa pode ser definida. Se k> 0, a função estará diminuindo em todos os números reais. E seu gráfico estará no 1º e 3º quadrante.
Caso contrário, se o valor de K for negativo ou menor que zero, a função será crescente e seu gráfico será encontrado no 2º e 4º quadrantes.
Como é calculado?
Existem diferentes contextos onde a definição da constante de proporcionalidade pode ser necessária. Nos diferentes casos, diferentes dados sobre o problema serão mostrados, onde o estudo destes finalmente renderá o valor de K.
De forma genérica, o acima mencionado pode ser recapitulado. Os valores de K correspondem a duas expressões dependendo do tipo de proporcionalidade presente:
- Direto: K = Y / X
- Inverso ou indireto: K = Y.X
De acordo com seu gráfico
Às vezes, o gráfico de uma função será apenas parcial ou totalmente conhecido. Nestes casos, será necessário, por meio de análise gráfica, determinar o tipo de proporcionalidade. Depois será necessário definir uma coordenada que permita verificar os valores de X e Y para aplicar à fórmula correspondente de K.
Os gráficos referentes às proporcionalidades diretas são lineares. Por outro lado, os gráficos de funções proporcionais inversas, geralmente assumem a forma de hipérboles.
De acordo com a tabela de valores
Em alguns casos, existe uma tabela de valores com os valores correspondentes a cada iteração da variável independente. Normalmente, isso implica na realização do gráfico, além de definir o valor de K.
De acordo com a expressão analítica
Retorna a expressão que define a função analiticamente. O valor de K pode ser resolvido diretamente ou também pode ser inferido da própria expressão.
Por regra direta ou composta de três
Em outros modelos de exercício, certos dados são apresentados, os quais se referem à relação entre os valores. Isso torna necessário aplicar a regra de três direta ou composta para definir outros dados necessários no exercício..
História
O conceito de proporcionalidade sempre existiu. Não só na mente e no trabalho dos grandes matemáticos, mas no dia a dia da população, devido à sua praticidade e aplicabilidade..
É muito comum encontrar situações que requerem uma abordagem de proporcionalidade. Estes são apresentados em cada caso onde é necessário comparar variáveis e fenômenos que possuem certas relações.
Por meio de uma linha do tempo podemos caracterizar os momentos históricos, nos quais os avanços matemáticos relativos à proporcionalidade foram aplicados..
- Século 2 aC O sistema de armazenamento de fração e proporção é adotado na Grécia.
- Século 5 aC A proporção que relaciona o lado e a diagonal de um quadrado também é descoberta na Grécia.
- 600 AC Tales de Mileto apresenta seu teorema sobre proporcionalidade.
- Ano 900. O sistema decimal usado anteriormente pela Índia é expandido em razões e proporções. Contribuição dos árabes.
- Século XVII. As contribuições referentes às proporções chegam ao cálculo de Euler.
- Século XIX. Gauss contribui com o conceito de número complexo e proporção.
- Século XX. A proporcionalidade como modelo de função é definida por Azcarate e Deulofeo.

Exercícios resolvidos
Exercício 1
É necessário calcular o valor das variáveis x, y, z e g. Conhecendo as seguintes relações proporcionais:
3x + 2y - 6z + 8g = 1925
x / 3 = y / 8 = z / 3 = g / 5
Passamos a definir os valores relativos da constante de proporcionalidade. Podem ser obtidos a partir da segunda relação, onde o valor que divide cada variável indica uma relação ou razão referente a K.
X = 3k y = 2k z = 3k g = 5k
Os valores são substituídos na primeira expressão, onde o novo sistema será avaliado em uma única variável k.
3 (3k) + 2 (2k) - 6 (3k) + 8 (5k) = 1925
9k + 4k -18k + 40k = 1925
35k = 1925
K = 1925/35 = 55
Usando este valor da constante de proporcionalidade podemos encontrar a figura que define cada uma das variáveis.
x = 3 (55) = 165 y = 2 (55) = 110
z = 3 (55) = 165 g = 5 (55) = 275
Exercício 2
Calcular a constante de proporcionalidade e a expressão que define a função, dado seu gráfico.
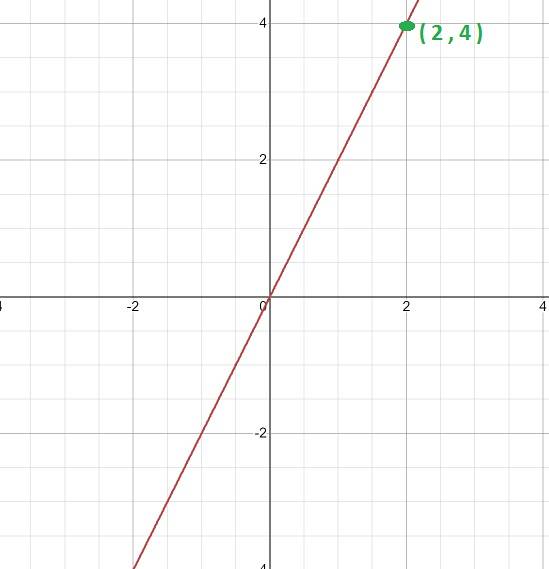
Em primeiro lugar, o gráfico é analisado, sendo evidente o seu caráter linear. Isso indica que se trata de uma função com proporcionalidade direta e que o valor de K será obtido através da expressão k = y / x
Em seguida, é escolhido um ponto determinável do gráfico, ou seja, aquele em que as coordenadas que o compõem podem ser visualizadas com exatidão..
Para este caso, o ponto (2, 4) é usado. De onde podemos estabelecer a seguinte relação.
K = 4/2 = 2
Portanto, a expressão é definida pela função y = kx, que neste caso será
F (x) = 2x
Referências
- Matemática para Eletricidade e Eletrônica. Dr. Arthur Kramer. Cengage Learning, 27 de julho 2012
- Visão 2020: O Papel Estratégico da Pesquisa Operacional. N. Ravichandran. Editores Aliados, 11 de setembro. 2005
- Conhecimentos de Gramática e Aritmética de Auxiliar Administrativo do Estado E-book. MAD-Eduforma
- Reforço da Matemática para apoio e diversificação curricular: para apoio e diversificação curricular. Mª Lourdes Lázaro Soto. Narcea Ediciones, 29 de agosto. 2003
- Logística e gestão comercial. Maria José Escudero Serrano. Ediciones Paraninfo, S.A., 1 set. 2013



Ainda sem comentários