
Exemplos de coordenadas esféricas e exercícios resolvidos

As coordenadas esféricas são um sistema de localização de pontos no espaço tridimensional que consiste em uma coordenada radial e duas coordenadas angulares chamadas de coordenada polar e coordenada de azimute.
A Figura 1, que vemos a seguir, mostra as coordenadas esféricas (r, θ, φ) de um ponto M. Essas coordenadas referem-se a um sistema ortogonal de eixos cartesianos X, Y, Z de origem O.
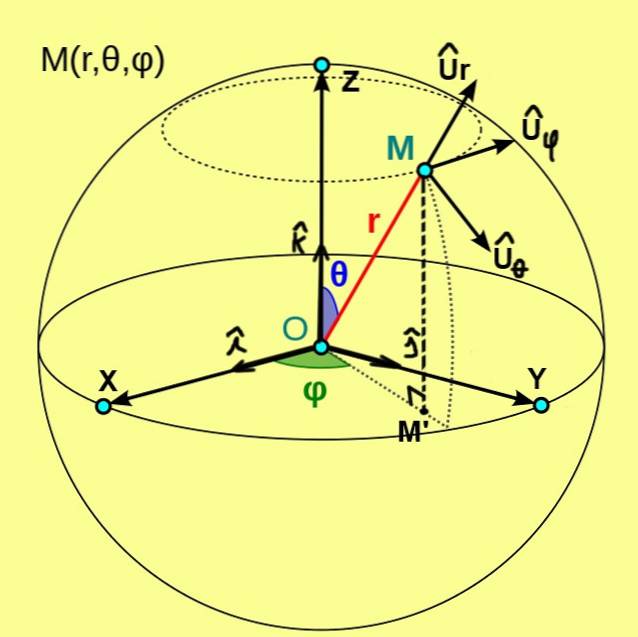
Nesse caso, a coordenada r do ponto M é a distância desse ponto até a origem O. A coordenada polar θ representa o ângulo entre o semieixo positivo Z e o vetor de raio OM. Enquanto a coordenada azimutal φ é o ângulo entre o semieixo positivo X e o vetor de raio OM ', onde M' é a projeção ortogonal de M no plano XY.
A coordenada radial r apenas assume valores positivos, mas se um ponto estiver localizado na origem, então r = 0. A coordenada polar θ assume como valor mínimo 0º para pontos localizados no semi-eixo Z positivo e um valor máximo 180º para os pontos está localizado no semi-eixo negativo Z. Finalmente, a coordenada azimutal φ assume como valor mínimo 0º e uma altura máxima de 360º.
0 ≤ r < ∞
0 ≤ θ ≤ 180º
0 ≤ φ < 360º
Índice do artigo
- 1 Mudança de coordenadas
- 1.1 Base vetorial em coordenadas esféricas
- 1.2 Elementos de linha e volume em coordenadas esféricas
- 2 Relacionamento com coordenadas geográficas
- 2.1 Fórmulas para mudar de geográfico para esférico
- 3 exemplos
- 3.1 Exemplo 1
- 3.2 Exemplo 2
- 4 exercícios
- 4.1 Exercício 1
- 4.2 Exercício 2
- 5 referências
Mudança de coordenadas
As fórmulas que permitem obter as coordenadas cartesianas (x, y, z) de um ponto M serão dadas a seguir, assumindo que as coordenadas esféricas do mesmo ponto (r, θ, φ) sejam conhecidas:
x = r Sen (θ) Cos (φ)
y = r Sen (θ) Sen (φ)
z = r Cos (θ)
Da mesma forma, é útil encontrar as relações para ir das coordenadas cartesianas (x, y, z) de um determinado ponto às coordenadas esféricas desse ponto:
r = √ (x ^ 2 + y ^ 2 + z ^ 2)
θ = Arctan (√ (x ^ 2 + y ^ 2) / z)
φ = Arctan (y / x)
Base vetorial em coordenadas esféricas
A partir das coordenadas esféricas, uma base ortonormal de vetores de base é definida, que são denotados por Ur, Uθ, Uφ. A Figura 1 mostra esses três vetores unitários, que possuem as seguintes características:
- Ur é o vetor unitário tangente à linha radial θ = ctte e φ = ctte;
- Uθ é o vetor unitário tangente ao arco φ = ctte e r = ctte;
- Uφ é o vetor unitário tangente ao arco r = ctte e θ = ctte.
Elementos de linha e volume em coordenadas esféricas
O vetor de posição de um ponto no espaço em coordenadas esféricas é escrito assim:
r = r Ur
Mas uma variação infinitesimal ou deslocamento de um ponto no espaço tridimensional, nessas coordenadas, é expressa pela seguinte relação vetorial:
dr = dr Ur + r dθ Uθ + r Sen (θ) dφ Uφ
Finalmente, um volume infinitesimal dV em coordenadas esféricas é escrito assim:
dV = r ^ 2 Sen (θ) dr dθ dφ
Essas relações são muito úteis para calcular integrais de linha e volume em situações físicas que têm simetria esférica..
Relacionamento com coordenadas geográficas
Por coordenadas geográficas entende-se aquelas que servem para localizar lugares na superfície terrestre. Este sistema usa as coordenadas de latitude e longitude para localizar a posição na superfície da Terra..
No sistema de coordenadas geográficas, a superfície da Terra é considerada esférica com raio Rt, embora seja conhecida por ser achatada nos pólos, e um conjunto de linhas imaginárias chamadas paralelas e meridianos é considerado.
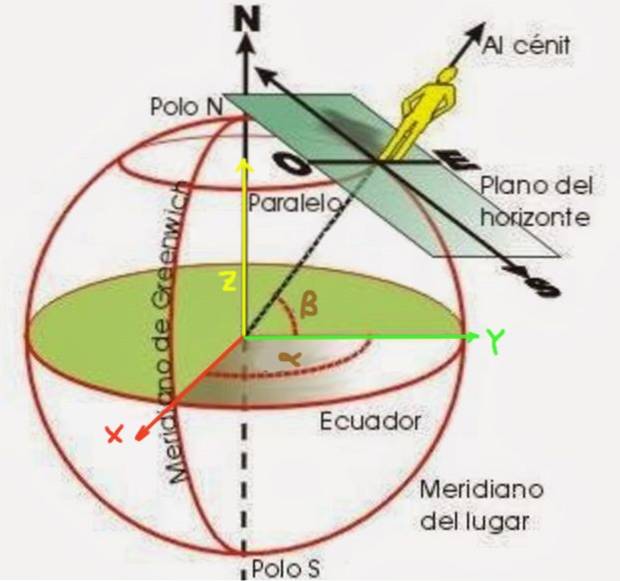
A latitude β é um ângulo formado por um raio que começa do centro da Terra até o ponto que você deseja posicionar. É medido a partir do plano equatorial, conforme mostrado na figura 2. Por outro lado, a longitude α é o ângulo que o meridiano do ponto que está sendo localizado forma em relação ao meridiano zero (conhecido como meridiano de Greenwich).
A latitude pode ser latitude norte ou sul, dependendo se o lugar que você está localizando está no hemisfério norte ou no hemisfério sul. Da mesma forma, a longitude pode ser oeste ou leste, dependendo se a localização é oeste ou leste do meridiano zero..
Fórmulas para mudar de geográfico para esférico
Para obter essas fórmulas, a primeira coisa é estabelecer um sistema de coordenadas. O plano XY é escolhido para coincidir com o plano equatorial, sendo o semi-eixo X positivo aquele que parte do centro da Terra e passa pelo meridiano zero. Por sua vez, o eixo Y passa pelo meridiano 90º E. A superfície da Terra tem um raio Rt.
Com este sistema de coordenadas, as transformações de geográfico para esférico são assim:
αEβN → (Rt, θ = 90º-β, φ = α)
αOβN → (Rt, θ = 90º-β, φ = 360º-α)
αEβS → (Rt, θ = 90º + β, φ = α)
αOβS → (Rt, θ = 90º + β, φ = 360º-α)
Exemplos
Exemplo 1
As coordenadas geográficas de Palma de Maiorca (Espanha) são:
Longitude Leste 38.847º e Latitude Norte 39.570º. Para determinar as coordenadas esféricas correspondentes a Palma de Maiorca, é aplicada a primeira das fórmulas da seção anterior:
38.847ºE39.570ºN → (r = 6371 km, θ = 90º-39.570º, φ = 38.847º)
Portanto, as coordenadas esféricas são:
Palma de Maiorca: (r = 6371 km, θ = 50,43º, φ = 38,85º)
Na resposta anterior, consideramos r igual ao raio médio da Terra.
Exemplo 2
Sabendo que as Ilhas Falkland (Malvinas) possuem coordenadas geográficas de 59ºO 51,75ºS, determine as coordenadas polares correspondentes. Lembre-se que o eixo X vai do centro da Terra ao meridiano 0º e no plano equatorial; o eixo Y também no plano equatorial e passando pelo meridiano 90º Oeste; finalmente, o eixo Z no eixo de rotação da Terra na direção Sul-Norte.
Para encontrar então as coordenadas esféricas correspondentes, usamos as fórmulas apresentadas na seção anterior:
59ºO 51,75ºS → (r = 6371 km, θ = 90º + 51,75º, φ = 360º-59º) que é
Malvinas: (r = 6371 km, θ = 141,75º, φ = 301º)
Treinamento
Exercício 1
Encontre as coordenadas cartesianas de Palma de Mallorca no sistema de referência cartesiano XYZ mostrado na figura 2.
Solução: Anteriormente, no exemplo 1, as coordenadas esféricas eram obtidas a partir das coordenadas geográficas de Palma de Maiorca. Portanto, as fórmulas apresentadas acima podem ser usadas para ir do esférico ao cartesiano:
x = 6371 km Sen (50,43º) Cos (38,85º)
y = 6371 km Sen (50,43º) Sen (38,85º)
z = 6371 km Cos (50,43º)
Realizando os cálculos correspondentes, temos:
Palma de Maiorca: (x = 3825 km, y = 3081 km, z = 4059)
Exercício 2
Encontre as coordenadas cartesianas das Ilhas Malvinas no sistema de referência cartesiano XYZ mostrado na figura 2.
Solução: Anteriormente, no exemplo 2, as coordenadas esféricas eram obtidas a partir das coordenadas geográficas das Ilhas Malvinas. Portanto, as fórmulas apresentadas acima podem ser usadas para ir do esférico ao cartesiano:
x = 6371 km Sen (141,75º) Cos (301º)
y = 6371 km Sen (141,75º) Sen (301º)
z = 6371 km Cos (141,75º)
Fazendo os cálculos correspondentes, obtemos:
Ilhas Malvinas: (x = 2031 km, y = -3381 km, z = -5003)
Referências
- Arfken G e Weber H. (2012). Métodos matemáticos para físicos. Um guia completo. 7ª edição. Academic Press. ISBN 978-0-12-384654-9
- Cálculo cc. Resolvidos problemas de coordenadas cilíndricas e esféricas. Recuperado de: calculo.cc
- Oficina de Astronomia. Latitude e longitude. Recuperado de: tarifamates.blogspot.com/
- Weisstein, Eric W. "Spherical Coordinates." Da MathWorld-A Wolfram Web. Recuperado de: mathworld.wolfram.com
- wikipedia. Sistema de coordenadas esféricas. Recuperado de: en.wikipedia.com
- wikipedia. Campos de vetores em coordenadas cilíndricas e esféricas. Recuperado de: en.wikipedia.com



Ainda sem comentários