
Exemplos de coordenadas retangulares e exercícios resolvidos
As coordenadas retangulares ou cartesianos são aqueles que se obtêm projetando ortogonalmente nos três eixos cartesianos X, Y, Z um ponto localizado no espaço tridimensional.
Os eixos cartesianos são linhas mutuamente orientadas perpendiculares entre si. No sistema de coordenadas cartesianas, cada ponto no espaço é atribuído a três números reais que são suas coordenadas retangulares.
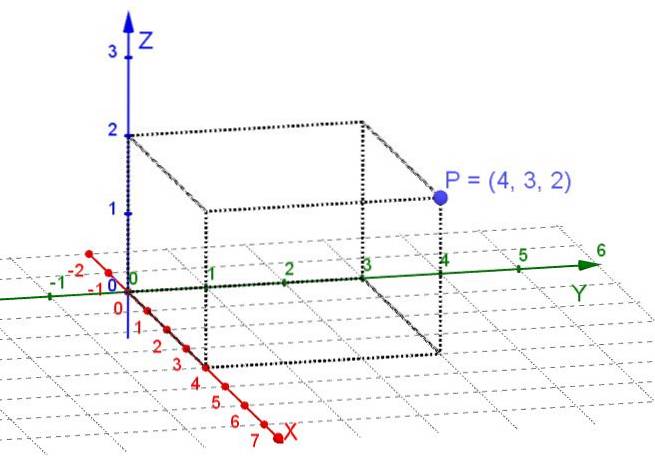
Um plano é um subespaço do espaço tridimensional. No caso de considerar pontos em um plano, basta escolher um par de eixos perpendiculares X, Y como sistema cartesiano. Então, cada ponto do plano é atribuído a dois números reais que são suas coordenadas retangulares.
Índice do artigo
- 1 Origem das coordenadas retangulares
- 2 O plano cartesiano
- 2.1 Distância entre dois pontos
- 2.2 Expressão analítica de uma linha
- 3 exemplos
- 3.1 Exemplo 1
- 3.2 Exemplo 2
- 4 exercícios resolvidos
- 4.1 Exercício 1
- 4.2 Exercício 2
- 5 referências
Origem das coordenadas retangulares
As coordenadas retangulares foram originalmente propostas pelo matemático francês René Descartes (1596 e 1650), por isso são chamadas de cartesianas.
Com esta ideia de Descartes, os pontos do plano e do espaço são atribuídos números, para que as figuras geométricas tenham uma equação algébrica associada e os teoremas geométricos clássicos possam ser provados algebricamente. Com as coordenadas cartesianas, nasce a geometria analítica.
O plano cartesiano
Se em um plano duas linhas perpendiculares são escolhidas que se cruzam em um ponto O; e se, além disso, a cada linha é atribuída uma direção e uma escala numérica entre pontos equidistantes sucessivos, então existe um sistema cartesiano ou plano no qual cada ponto do plano está associado a um par ordenado de dois números reais que são suas projeções respectivamente nos eixos X e Y.
Os pontos A = (3, 2); B = (- 2, 3); C = (- 2, -3) e D = (3, -3) são representados no plano cartesiano conforme mostrado abaixo:
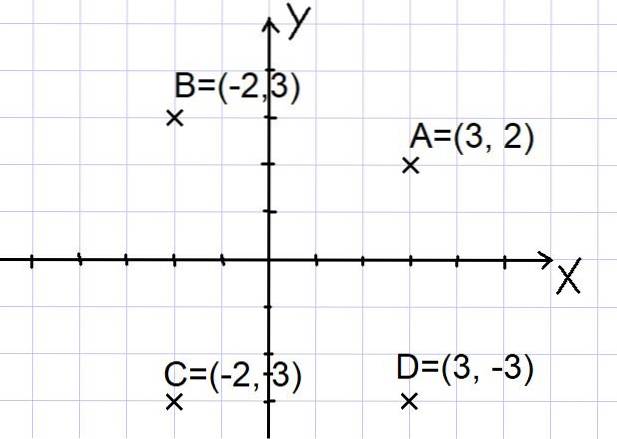
Observe que os dois eixos X e Y dividem o plano em quatro setores chamados quadrantes. O ponto A está no primeiro quadrante, B está no segundo quadrante, C está no terceiro quadrante e o ponto D está no quarto quadrante..
Distância entre dois pontos
A distância entre dois pontos A e B no plano cartesiano é o comprimento do segmento que os une. Esta distância pode ser calculada analiticamente da seguinte forma:
d (A, B) = √ (Bx - Ax) ^ 2 + (Por - Ay) ^ 2)
A fórmula acima é obtida aplicando o teorema de Pitágoras.
Aplicando esta fórmula aos pontos A, B na figura 2, temos:
d (A, B) = √ (-2 - 3) ^ 2 + (3 - 2) ^ 2) = √ (-5) ^ 2 + 1 ^ 2) = √ (26)
Ou seja, d (A, B) = 5,10 unidades. Observe que a distância foi obtida sem a necessidade de medir com uma régua, um procedimento totalmente algébrico foi seguido.
Expressão analítica de uma linha
As coordenadas retangulares permitem a representação analítica de objetos geométricos fundamentais, como o ponto e a linha. Dois pontos A e B definem uma única linha. A inclinação da linha é definida como o quociente entre a diferença das coordenadas Y do ponto B menos A, dividido pela diferença das coordenadas X do ponto B menos A:
inclinação = (Por - Ay) / (Bx - Ax)
Qualquer ponto P de coordenadas (x, y) que pertença à reta (AB) deve ter a mesma inclinação:
inclinação = (y - Ay) / (x - Ax)
A equação que se obtém por meio da igualdade das inclinações é a representação analítica ou algébrica da reta que passa pelos pontos A e B:
(y - Ay) / (x - Ax) = (By - Ay) / (Bx - Ax).
Se tomarmos para A e B as coordenadas retangulares da figura 2, temos:
(y - 2) / (x - 3) = (3 - 2) / (- 2 - 3)
(y - 2) / (x - 3) = -⅕
Neste caso particular, temos uma linha com uma inclinação negativa -⅕, o que significa que ao localizar em um ponto na linha e aumentar a coordenada x em uma unidade, a coordenada y diminui em 0,2 unidades.
A maneira mais comum de escrever a equação da reta no plano é com a coordenada y apagada em função da variável x:
y = - (1/5) x + 13/5
Exemplos
Exemplo 1
Obtenha por métodos analíticos a distância entre os pontos C e A, sendo as coordenadas retangulares de C = (-2, -3) e de A = (3,2)..
A fórmula para a distância euclidiana entre esses dois pontos é escrita assim:
d (A, C) = √ ((Cx - Ax) ^ 2 + (Cy - Ay) ^ 2)
Substituindo suas coordenadas retangulares correspondentes, temos:
d (A, C) = √ (-2 - 3) ^ 2 + (-3 - 2) ^ 2) = √ (-5) ^ 2 + (-5) ^ 2) = 5√2 = 7,07
Exemplo 2
Obtenha a equação da reta que passa pelo ponto C das coordenadas (-2, -3) e pelo ponto P das coordenadas (2, 0).
Primeiro, a inclinação da linha CP é obtida:
inclinação = (0 - (- 3)) / (2 - (-2)) = ¾
Qualquer ponto Q de coordenadas retangulares genéricas (x, y) que pertence à linha CP deve ter a mesma inclinação:
inclinação = (y - (- 3)) / (x - (-2)) = (y +3) / (x +2)
Em outras palavras, a equação da linha CP é:
(y +3) / (x +2) = ¾
Uma maneira alternativa de escrever a equação da linha que CP está resolvendo para y:
y = ¾ x - 3/2
Exercícios resolvidos
Exercício 1
Obtenha as coordenadas retangulares do ponto de intersecção entre as linhas y = - (1/5) x + 13/5 e a linha y = ¾ x - 3/2.
Solução: Por definição, o ponto de interseção das duas linhas compartilham as mesmas coordenadas retangulares. Portanto, as coordenadas y no ponto de interseção são idênticas para ambas as linhas:
-(1/5) x + 13/5 = ¾ x - 3/2
o que leva à seguinte expressão:
(¾ + ⅕) x = 13/5 +3/2
resolvendo a soma das frações, obtemos:
19/20 x = 41/10
Resolvendo para x:
x = 82/19 = 4,32
Para obter a interceptação y, o valor x obtido é substituído em qualquer uma das linhas:
y = ¾ 4,32 - 3/2 = 1,74
Isso significa que as linhas dadas se cruzam no ponto I das coordenadas I = (4.32, 1.74).
Exercício 2
Obtenha a equação da circunferência que passa pelo ponto R de coordenadas retangulares (3, 4) e que tem seu centro na origem das coordenadas.
Solução: O raio R é a distância do ponto R à origem O das coordenadas (0, 0).
d (R, O) = √ ((Rx - 0) ^ 2 + (Ry - 0) ^ 2) = √ ((3 - 0) ^ 2 + (4 - 0) ^ 2) = √ (3 ^ 2 + 4 ^ 2) = √ (9 + 16) = √ (25) = 5
Ou seja, é um círculo de raio 5 centrado em (0,0).
Qualquer ponto P (x, y) na circunferência deve ter a mesma distância 5 do centro (0, 0) para que possa ser escrito:
d (P, O) = √ ((x - 0) ^ 2 + (y - 0) ^ 2) = √ (x ^ 2 + y ^ 2) = 5
Quer dizer:
√ (x ^ 2 + y ^ 2) = 5
Para eliminar a raiz quadrada, ambos os membros da igualdade são elevados ao quadrado, obtendo:
x ^ 2 + y ^ 2 = 25
Qual é a equação da circunferência.
Este exemplo ilustra a força do sistema de coordenadas retangulares, que permite determinar objetos geométricos, como a circunferência, sem a necessidade do uso de papel, lápis e compasso. A circunferência solicitada foi determinada exclusivamente por métodos algébricos.
Referências
- Arfken G e Weber H. (2012). Métodos matemáticos para físicos. Um guia completo. 7ª edição. Academic Press. ISBN 978-0-12-384654-9
- Cálculo cc. Resolvidos problemas de coordenadas retangulares. Recuperado de: calculo.cc
- Weisstein, Eric W. "Cartesian Coordinates". Da MathWorld-A Wolfram Web. Recuperado de: mathworld.wolfram.com
- wikipedia. Sistema de coordenada cartesiana. Recuperado de: en.wikipedia.com



Ainda sem comentários