Comprimento do acorde (geometria), teorema e exercícios

UMA fragmento, na geometria plana, é o segmento de linha que une dois pontos em uma curva. A linha que contém este segmento é considerada uma linha secante da curva. Geralmente é um círculo, mas os acordes podem certamente ser desenhados em muitas outras curvas, como elipses e parábolas..

Na figura 1 à esquerda há uma curva, à qual pertencem os pontos A e B. O acorde entre A e B é o segmento verde. À direita está uma circunferência e uma de suas cordas, já que é possível desenhar infinitas.

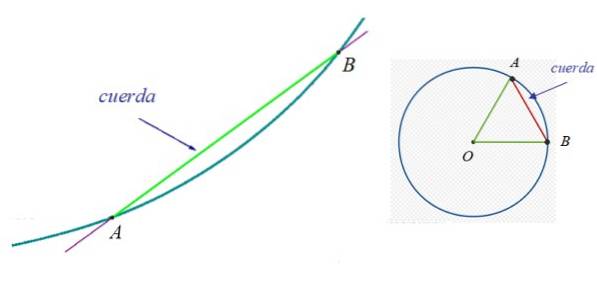
Na circunferência seu diâmetro é particularmente interessante, também conhecido como acorde maior. É um acorde que sempre contém o centro da circunferência e mede o dobro do raio.

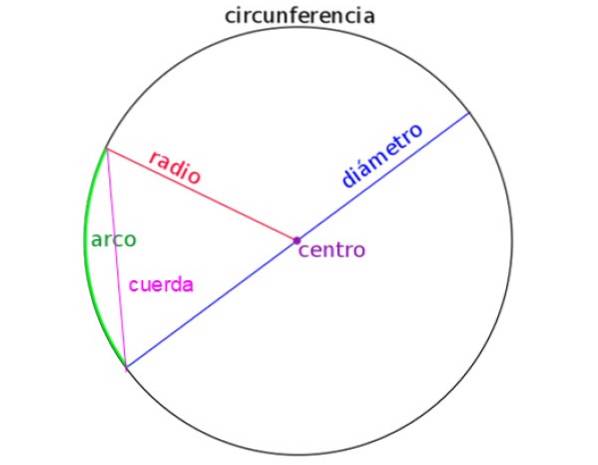
A figura a seguir mostra o raio, o diâmetro, uma corda e também o arco de um círculo. Identificar corretamente cada um é importante ao resolver problemas.

Índice do artigo

• 1 comprimento de corda de uma circunferência
  • 1.1 Teorema das cordas 
• 2 exercícios resolvidos de cordas
  • 2.1 - Exercício 1
  • 2.2 - Exercício 2
• 3 referências

Comprimento da corda de uma circunferência

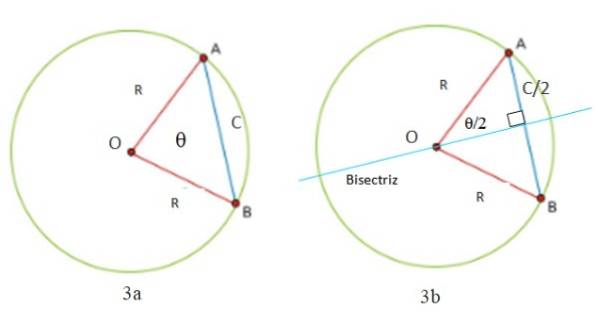
Podemos calcular o comprimento da corda em um círculo a partir das Figuras 3a e 3b. Observe que um triângulo é sempre formado por dois lados iguais (isósceles): segmentos OA e OB, que medem R, o raio da circunferência. O terceiro lado do triângulo é o segmento AB, chamado C, que é precisamente o comprimento da corda.

É necessário traçar uma linha perpendicular à corda C para bissectar o ângulo θ que existe entre os dois raios e cujo vértice é o centro O da circunferência. Este é um ângulo central -porque seu vértice é o centro - e a linha bissetriz também é uma secante à circunferência.

Imediatamente são formados dois triângulos retângulos, cuja hipotenusa mede R. Como a bissetriz, e com ela o diâmetro, divide a corda em duas partes iguais, verifica-se que uma das pernas é a metade de C, conforme indicado na figura 3b.

A partir da definição do seno de um ângulo:

sin (θ / 2) = perna oposta / hipotenusa = (C / 2) / R

Portanto:

sin (θ / 2) = C / 2R

C = 2R sen (θ / 2)

Teorema das cordas 

O teorema das cordas é assim:

Se quaisquer duas cordas de um círculo se cruzam em um ponto, o produto do comprimento dos segmentos que aparecem em uma das cordas é igual ao produto dos comprimentos dos segmentos que são definidos na outra corda..

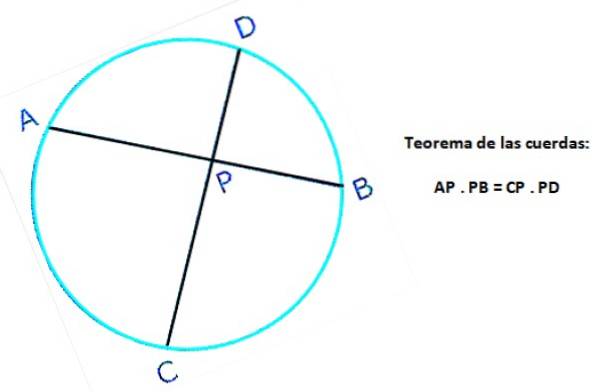
A figura a seguir mostra dois acordes da mesma circunferência: AB e CD, que se cruzam no ponto P. No acorde AB os segmentos AP e PB são definidos, enquanto no acorde CD CP e PD são definidos. Então, de acordo com o teorema:

AP. PB = CP. P.S.

Exercícios resolvidos de cordas

- Exercício 1

Uma circunferência tem uma corda de 48 cm, que está a 7 cm do centro. Calcule a área do círculo e o perímetro da circunferência.

Solução  

Para calcular a área do círculo A, basta saber o raio da circunferência ao quadrado, pois é verdade:

A = π.R^dois

Agora, a figura que se forma com os dados fornecidos é um triângulo retângulo, cujas pernas têm 7 e 24 cm respectivamente.

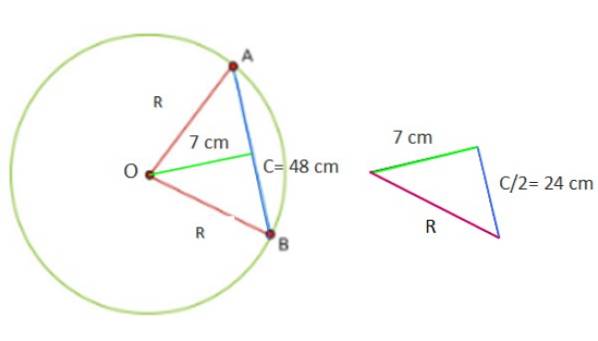
Portanto, para encontrar o valor de R^dois o teorema de Pitágoras é aplicado diretamente c^dois = a^dois + b^dois, uma vez que R é a hipotenusa do triângulo:

R^dois = (7 cm)^dois + (24 cm)^dois = 625 cm^dois

Portanto, a área solicitada é:

A = π. 625 cm^dois = 1963,5 cm^dois

Em relação ao perímetro ou comprimento L da circunferência, é calculado por:

L = 2π. R

Substituindo valores:

R = √625 cm^dois = 25 cm

L = 2π. 25 cm = 157,1 cm.

- Exercício 2

Determine o comprimento da corda de um círculo cuja equação é:

x^dois + Y^dois - 6x - 14a -111 = 0

As coordenadas do ponto médio do acorde são conhecidas como P (17/2; 7/2).

Solução

O ponto médio do acorde P não pertence à circunferência, mas os pontos finais do acorde sim. O problema pode ser resolvido por meio do teorema das cordas previamente declarado, mas primeiro é conveniente escrever a equação da circunferência na forma canônica, para determinar seu raio R e seu centro O.

Etapa 1: obtenha a equação canônica da circunferência

A equação canônica do círculo com centro (h, k) é:

(x-h)^dois + (e que)^dois = R^dois

Para obtê-lo, é necessário preencher quadrados:

(x^dois - 6x) + (e^dois - 14y) -111 = 0

Observe que 6x = 2. (3x) e 14y = 2. (7y), de modo que a expressão anterior é reescrita assim, permanecendo inalterada:

(x^dois - 6x + 3^dois-3^dois) + (e^dois - 14a + 7^dois-7^dois) -111 = 0

E agora, lembrando a definição de produto notável (a-b)^dois = a^dois - 2ab + b^dois Pode ser escrito:

(x - 3)^dois - 3^dois + (e - 7)^dois - 7^dois - 111 = 0

= (x - 3)^dois + (e - 7)^dois = 111 + 3^dois + 7^dois → (x - 3)^dois + (e - 7)^dois = 169

A circunferência tem centro (3,7) e raio R = √169 = 13. A figura a seguir mostra o gráfico da circunferência e os acordes que serão usados ​​no teorema:

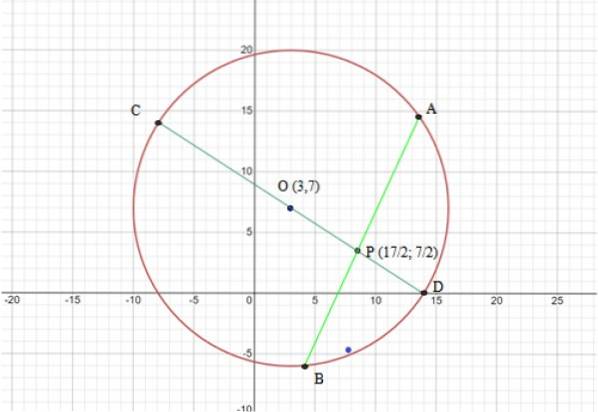
Etapa 2: determinar os segmentos a serem usados ​​no teorema das cordas

Os segmentos a serem utilizados são as strings CD e AB, conforme figura 6, ambas são cortadas no ponto P, portanto:

CP. PD = AP. PB

Agora vamos encontrar a distância entre os pontos O e P, pois isso nos dará o comprimento do segmento OP. Se adicionarmos o raio a este comprimento, teremos o segmento CP.

A distância d_OP entre dois pontos coordenados (x₁,Y₁) e (x_dois,Y_dois) isso é:

d_OP^dois = OP^dois = (x_dois - x₁)^dois + (Y_dois - Y₁)^dois = (3-17 / 2)^dois + (7/7/2)^dois = 121/4 + 49/4 = 170/4

d_OP = OP = √170 / 2

Com todos os resultados obtidos, mais o gráfico, construímos a seguinte lista de segmentos (ver figura 6):

CO = 13 cm = R

OP = √170 / 2 cm

CP = OP + R = 13 + √170 / 2 cm

PD = OD - OP = 13 - √170 / 2 cm

AP = PB

2.AP = comprimento do acorde

Substituindo no teorema das cordas:

CP. PD = AP. PB = [(13 + √170 / 2). (13 -√170 / 2)] = AP^dois

[169 -170/4] = AP^dois

253/2 = AP^dois

AP = √ (253/2)

O comprimento do acorde é 2.AP = 2 (√253 / 2) = √506

O leitor poderia resolver o problema de outra maneira?

Referências

1. Baldor, A. 2004. Geometria plana e espacial com trigonometria. Publicaciones Cultural S.A. de C.V. México.
2. C-K12. Comprimento de um acorde. Recuperado de: ck12.org.
3. Escobar, J. The Circumference. Recuperado de: matematicas.udea.edu.co.
4. Villena, M. Cónicas. Recuperado de: dspace.espol.edu.ec.
5. Wikipedia. Corda (geometria). Recuperado de: es.wikipedia.org.