
Exemplos de dados agrupados e exercícios resolvidos
O dados agrupados são aqueles que foram classificados em categorias ou classes, tendo como critério a sua frequência. Isso é feito para simplificar o tratamento de grandes quantidades de dados e estabelecer suas tendências..
Uma vez organizados nessas classes por suas frequências, os dados constituem um distribuição de frequência, do qual informações úteis são extraídas por meio de suas características.

Aqui está um exemplo simples de dados agrupados:
Suponha que a altura de 100 alunas, selecionadas de todos os cursos básicos de física de uma universidade, seja medida e os seguintes resultados sejam obtidos:

Os resultados obtidos foram divididos em 5 classes, que aparecem na coluna da esquerda.
A primeira turma, entre 155 e 159 cm, tem 6 alunos, a segunda turma 160 - 164 cm tem 14 alunos, a terceira turma de 165 a 169 cm tem o maior número de membros: 47. A seguir a turma continua 170-174 cm com 28 alunos e finalmente o 175-174 cm com apenas 5.
O número de membros de cada classe é precisamente o frequência ou Frequência absoluta e ao adicionar todos eles, o total de dados é obtido, que neste exemplo é 100.
Índice do artigo
- 1 Características da distribuição de frequência
- 1.1 Freqüência
- 1.2 Limites
- 1.3 Fronteiras
- 1.4 Amplitude
- 1.5 marca de classe
- 2 Medidas de tendência central e dispersão para dados agrupados
- 2.1 Média
- 2,2 mediana
- 2.3 Moda
- 2.4 Variância e desvio padrão
- 3 Exercício resolvido
- 3.1 Solução a
- 3.2 Solução b
- 3.3 Solução d
- 4 referências
Características da distribuição de frequência
Frequência
Como vimos, a frequência é o número de vezes que um dado é repetido. E para facilitar os cálculos das propriedades da distribuição, como média e variância, são definidas as seguintes quantidades:
-Frequência acumulativa: é obtido somando a frequência de uma classe com a frequência acumulada anterior. A primeira de todas as frequências corresponde ao intervalo em questão e a última é o número total de dados.
-Frequência relativa: calculado dividindo a frequência absoluta de cada classe pelo número total de dados. E se você multiplicar por 100, você tem a frequência percentual relativa.
-Frequência relativa cumulativa: é a soma das frequências relativas de cada classe com as anteriores acumuladas. A última das frequências relativas acumuladas deve ser igual a 1.
Para nosso exemplo, as frequências são assim:
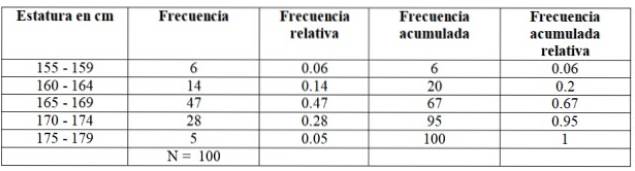
Limites
Os valores extremos de cada classe ou intervalo são chamados limites de classe. Como podemos ver, cada classe possui um limite inferior e um superior. Por exemplo, a primeira aula do estudo sobre alturas tem um limite inferior de 155 cm e um limite superior de 159 cm..
Este exemplo tem limites claramente definidos, porém é possível definir limites abertos: se em vez de definir os valores exatos, diga "altura menor que 160 cm", "altura menor que 165 cm" e assim por diante.
Fronteiras
A altura é uma variável contínua, portanto, pode-se considerar que a primeira classe na verdade começa em 154,5 cm, pois o arredondamento desse valor para o inteiro mais próximo dá 155 cm.
Esta classe abrange todos os valores até 159,5 cm, pois após isso, as alturas são arredondadas para 160,0 cm. Uma altura de 159,7 cm já pertence à seguinte classe.
Os limites reais da classe para este exemplo são, em cm:
- 154,5 - 159,5
- 159,5 - 164,5
- 164,5 - 169,5
- 169,5 - 174,5
- 174,5 - 179,5
Amplitude
A largura de uma classe é obtida subtraindo os limites. Para o primeiro intervalo do nosso exemplo, temos 159,5 - 154,5 cm = 5 cm.
O leitor pode verificar que para os demais intervalos do exemplo a amplitude também é de 5 cm. No entanto, deve-se notar que as distribuições podem ser construídas com intervalos de diferentes amplitudes.
Marca de classe
É o ponto médio do intervalo e é obtido pela média entre o limite superior e o limite inferior.
Para o nosso exemplo, a marca da primeira classe é (155 + 159) / 2 = 157 cm. O leitor pode ver que as demais marcas da classe são: 162, 167, 172 e 177 cm.
Determinar as notas da classe é importante, pois são necessárias para encontrar a média aritmética e a variância da distribuição.
Medidas de tendência central e dispersão para dados agrupados
As medidas de tendência central mais comumente usadas são a média, a mediana e a moda, e descrevem com precisão a tendência dos dados de se agruparem em torno de um determinado valor central..
Metade
É uma das principais medidas de tendência central. Nos dados agrupados, a média aritmética pode ser calculada usando a fórmula:

-X é a média
-Feu é a frequência da aula
-meu é a marca da classe
-g é o número de classes
-n é o número total de dados
Mediana
Para a mediana é necessário identificar o intervalo onde se encontra a observação n / 2. Em nosso exemplo, esta observação é o número 50, porque há um total de 100 pontos de dados. Esta observação está na faixa de 165-169 cm.
Então você tem que interpolar para encontrar o valor numérico que corresponde a essa observação, para a qual a fórmula é usada:

Onde:
-c = largura do intervalo onde a mediana é encontrada
-BM = o limite inferior do intervalo ao qual a mediana pertence
-Fm = número de observações contidas no intervalo mediano
-n / 2 = metade dos dados totais
-FBM = número total de observações antes intervalo mediano
moda
Para o modo, é identificada a classe modal, aquela que contém mais observações, cuja marca de classe é conhecida.
Variância e desvio padrão
A variância e o desvio padrão são medidas de dispersão. Se denotarmos a variação com sdois e o desvio padrão, que é a raiz quadrada da variância como s, para dados agrupados teremos respectivamente:

Y

Exercício resolvido
Para a distribuição de alturas de universitárias propostas no início, calcule os valores de:
a) Média
b) mediana
c) Moda
d) Variância e desvio padrão.

Solução para
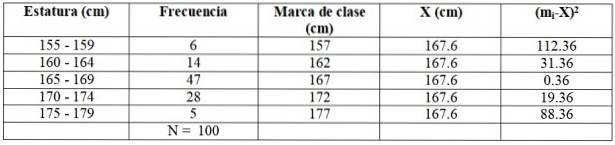
Vamos construir a seguinte tabela para facilitar os cálculos:


Substituindo valores e realizando a soma diretamente:
X = (6 x 157 + 14 x 162 + 47 x 167 + 28 x 172+ 5 x 177) / 100 cm =
= 167,6 cm
Solução b
O intervalo ao qual pertence a mediana é de 165-169 cm por ser o intervalo com maior frequência.

Vamos identificar cada um desses valores no exemplo, com a ajuda da Tabela 2:
c = 5 cm (veja a seção de amplitude)
BM = 164,5 cm
Fm = 47
n / 2 = 100/2 = 50
FBM = 20
Substituindo na fórmula:
O intervalo que contém a maioria das observações é de 165-169 cm, cuja marca de classe é de 167 cm.
Solução d
Expandimos a tabela anterior adicionando duas colunas adicionais:

Aplicamos a fórmula:

E desenvolvemos o somatório:
sdois = (6 x 112,36 + 14 x 31,36 + 47 x 0,36 + 28 x 19,36 + 5 x 88,36) / 99 = = 21,35 cmdois
Portanto:
s = √21,35 cmdois = 4,6 cm
Referências
- Berenson, M. 1985. Statistics for management and economics. Interamericana S.A.
- Canavos, G. 1988. Probabilidade e Estatística: Aplicações e métodos. Colina Mcgraw.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8º. Edição. Cengage.
- Levin, R. 1988. Statistics for Administrators. 2ª Edição. Prentice Hall.
- Spiegel, M. 2009. Estatísticas. Schaum series. 4º Edição. Colina Mcgraw.
- Walpole, R. 2007. Probabilidade e Estatística para Engenharia e Ciências. Pearson.



Ainda sem comentários