
Densidade
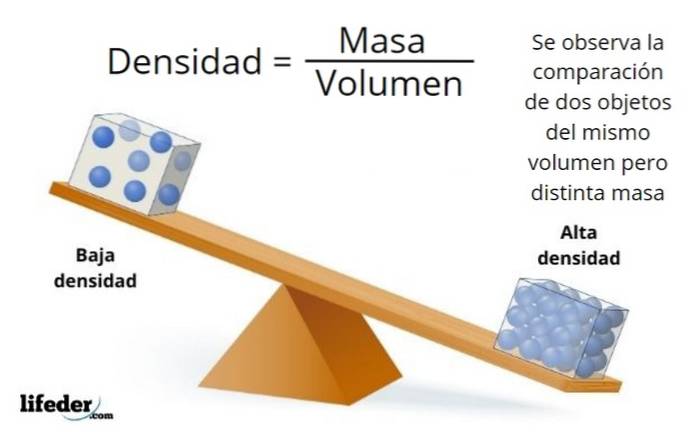
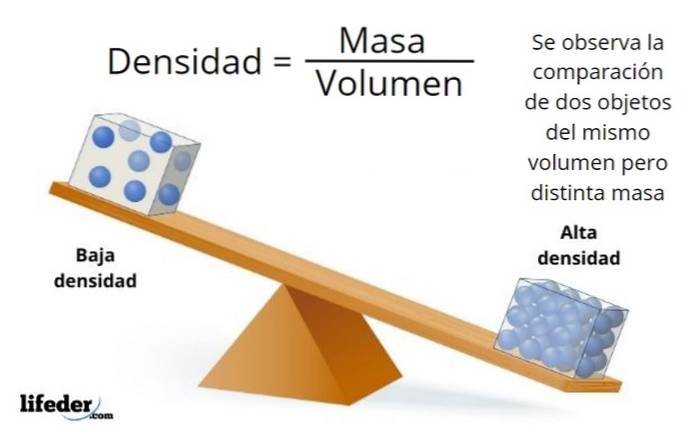
O que é densidade?
O densidade A massa de uma substância é o quociente entre a massa da amostra e o volume que ela ocupa, sendo sua unidade de medida kg / m3 no Sistema Internacional de Unidades. A letra grega ρ (rho) é freqüentemente usada para denotá-lo.
A densidade da água, que é o fluido universal, é 1000 kg / m3 ou 1 g / cm3 a 25 ºC, uma vez que a densidade sofre alterações com a temperatura e pressão.
Muitas vezes são encontrados objetos com as mesmas dimensões, mas alguns são mais leves e outros mais pesados, isso se deve às diferenças de densidade. O objeto mais leve tem uma densidade menor do que o mais pesado.
A densidade é uma propriedade intensiva da matéria, que não depende da quantidade de massa da amostra a ser examinada, pois é a relação massa / volume que permanece constante para a mesma substância. Isso torna possível diferenciar uma substância de outra.
Os materiais possuem uma ampla gama de densidades, as mais baixas são as dos gases, portanto a unidade kg / m3 é muito grande e gramas / litro ou g / L são os preferidos. Outras unidades usadas com frequência são gramas / mililitro ou gramas / centímetro cúbico.
O conceito de densidade é especialmente útil ao trabalhar com meios contínuos, como fluidos, sejam eles gases ou líquidos..
Fórmula de densidade
De acordo com a definição dada, a densidade tem uma fórmula matemática dada por:

Onde a densidade é ρ, m é a massa e V é o volume.
Como você mede a densidade?
A densidade de um objeto pode ser calculada se sua massa e volume forem medidos previamente. Este último nem sempre é fácil, pois a amostra pode ser irregular, porém existem vários métodos.
Método geométrico
Se a amostra tem uma forma geométrica regular, existem fórmulas que permitem que o volume seja calculado com base em suas dimensões. Quanto à massa, esta pode ser obtida com o auxílio de uma balança.
Método do tubo de ensaio: deslocamento de volume

Se o objeto não for regular, seu volume pode ser determinado medindo o volume deslocado, submergindo-o completamente em um fluido como a água..
Para isso, é utilizado um recipiente graduado e preenchido com um volume exato de água V1, então o objeto está completamente submerso e o novo volume V é medidodois. O volume do objeto é igual à diferença Vdois - V1.
Para usar este método, a substância da amostra não deve se dissolver na água e um recipiente graduado do tamanho apropriado deve estar disponível..
Densidade usando o princípio de Arquimedes
O princípio de Arquimedes pode ser usado para encontrar a densidade de uma amostra sólida. O princípio afirma que um corpo parcialmente ou totalmente submerso em um fluido experimenta uma força ascendente denominada empuxo, cuja magnitude é igual ao peso do fluido deslocado ao colocar o corpo.
Para determinar a densidade de um objeto usando o princípio de Arquimedes, as seguintes etapas são seguidas:
-
Passo 1
Determine a massa mc do objeto usando uma escala.
-
Passo 2
Encha um recipiente com um fluido de densidade conhecida, que geralmente é água destilada. Este valor é chamado de m1.
-
etapa 3
Mergulhe completamente o objeto sólido no recipiente com água, tomando cuidado para que não toque nas paredes. Observa-se que o fluido exerce um impulso E no sólido para cima, e este por sua vez, pela terceira lei de Newton, exerce uma reação de igual magnitude sobre a água, mas na direção oposta.
Ao pesar o conjunto, o valor obtido, denominado mdois, será o do recipiente cheio de água mais esta reação.
-
Passo 4
A partir da equação da densidade, podemos expressar o volume V do corpo, que é igual ao volume de fluido deslocado:

A massa do fluido desalojado mF É simplesmente:
mF = mdois −m1
Portanto:

Tipos de densidade
Densidade absoluta
É a densidade conforme definido acima: a razão da massa para o volume da amostra.

Densidade relativa
Ligue também gravidade específica, É a densidade de uma substância em relação a outra que é tomada como referência. Para sólidos e líquidos, esta substância de referência é água a 4ºC e 1 atm de pressão e para gases é ar seco. É calculado por:
Densidade relativa = densidade do material / densidade da água
Tanto a densidade do material quanto a da água devem ser medidas nas mesmas condições de pressão e temperatura e expressas nas mesmas unidades..
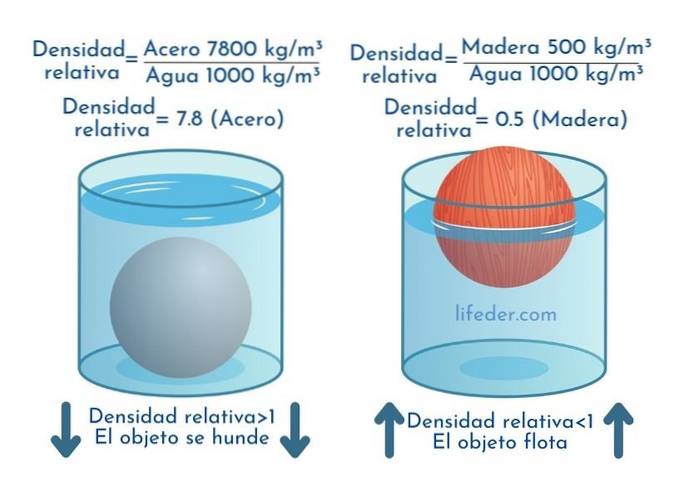
A imagem a seguir mostra as densidades relativas de aço e madeira.

Uma vez que a densidade do aço é 7800 kg / m3 e o da água é de 1000 kg / m3, A densidade relativa do aço, denotada como sg, é:
sg = 7800/1000 = 7,8
Por sua vez, a densidade relativa da madeira é:
sg = 500/1000 = 0,5
Objetos cuja densidade relativa é menor que 1 flutuam na água, enquanto aqueles cuja densidade relativa é maior que 1 afundam.
Densidade aparente
É calculado pelo quociente entre a massa da amostra e seu volume, incluindo poros e espaços com ar:
Densidade aparente = Massa / Volume = (Massa partículas + Massa ar ) / (Volume partículas+ Volume ar)
Exemplos de densidade
- O metal mais leve de todos é o lítio, com densidade de 530 kg / m3
- A densidade do sangue é 1060 kg / m3
- Ósmio é o metal mais denso conhecido, com uma densidade de 22 570 kg / m3
- O plasma quark tem uma densidade de 1 × 1019 kg / m3
Exercícios resolvidos
Exercício 1
Calcule a densidade da cortiça, sabendo que um cubo feito com este material, que mede 1,5 cm de lado, tem uma massa de 1 g.
-
Solução
O volume de um cubo é:
V = ℓ3 = (1,5 cm)3 = 3,375 cm3
O enunciado indica que a massa m do cubo é m = 1 g, portanto, substituindo valores na equação de densidade:
ρ = m / V = 1g / 3,375 cm3 = 0,296 g / cm3
Exercício 2
Qual é a massa de uma esfera de ósmio com raio de 15 cm?
-
Solução
A partir da equação da densidade:

A massa é apagada como:
m = ρ ∙ V
É necessário calcular o volume da esfera, que é dado pela fórmula:
Onde r é o raio da esfera. Uma vez que a densidade do ósmio é 22570 kg / m3, É conveniente expressar os 15 cm em metros:
r = 15 cm = 15 × 10-2 m
V = (4/3) π × (15 × 10-2 m)3 = 0,01414 m3
Este valor é substituído na folga pela massa:
m = ρ ∙ V = 22570 kg / m3 × 0,01414 m3 = 319,1 kg
Referências
- Chang, R. 2013. Chemistry. 11º. Edição. McGraw Hill Education.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall.
- Shipman, J. 2009. An Introduction to Physical Science. Décima segunda edição. Brooks / Cole, Edições Cengage.
- Tippens, P. 2011. Physics: Concepts and Applications. 7ª Edição. Colina Mcgraw.
- Universidade de Antioquia. Densidade de sólidos. Recuperado de: docencia.udea.edu.co.


Ainda sem comentários