O densidade aparente de uma amostra é definido como o quociente entre sua massa e o volume inalterado, que inclui todos os espaços ou poros que contém. Se houver ar nesses espaços, a densidade aparente ρb, ou densidade aparente isso é:
ρb = Massa / Volume = Massa partículas + Massa ar /Volume partículas+ Volume ar
Ao calcular a densidade aparente de uma amostra de solo, esta deve ser previamente seca em estufa a 105 ºC até que a massa fique constante, indicando que todo o ar evaporou..
De acordo com esta definição, a densidade aparente dos solos ou densidade seca, é calculado desta forma:
ρs = Peso de elementos sólidos / Volume sólido + Volume poros
Denotando como Ms para peso seco ou massa e Vt = Vs + Vp como o volume total, a fórmula é:
ρs = Ms / Vt
Índice do artigo
As unidades de densidade aparente no Sistema Internacional de Unidades são kg / m3. No entanto, outras unidades, como g / cm3 e megagramas / metro cúbico: Mg / m3 também são amplamente usados.
O conceito de densidade aparente é muito útil quando se trata de materiais heterogêneos e porosos como os solos, pois é indicativo de sua capacidade de drenagem e aeração, entre outras qualidades..
Por exemplo, solos pouco porosos têm altas densidades aparentes, são compactos e tendem a inundar facilmente, ao contrário dos solos porosos..
Quando há água ou outro fluido nos poros da amostra, o volume após a secagem diminui, portanto, ao fazer os cálculos, é necessário saber a proporção original da água (ver exemplo resolvido).
A densidade aparente dos materiais em geral, incluindo o solo, é muito variável, visto que existem fatores como o grau de compactação, a presença de matéria orgânica, sua textura, estrutura, profundidade e outros, que afetam a forma e a forma. de espaços de poros.
Os solos são definidos como uma mistura heterogênea de substâncias inorgânicas, substâncias orgânicas, ar e água. Ao toque eles podem ser textura fino, médio ou grosso, enquanto as partículas componentes podem ser organizadas de várias maneiras, um parâmetro conhecido como estrutura.
Solos finos e bem estruturados com alto percentual de matéria orgânica tendem a ter baixos valores de densidade aparente. Ao contrário, solos espessos, com menos matéria orgânica e pouca estrutura, tendem a ter valores mais elevados..
De acordo com sua textura, a densidade aparente possui os seguintes valores:
| Textura | Densidade aparente (g / cm3) |
|---|---|
| Multar | 1,00 - 1,30 |
| Mediana | 1,30 - 1,50 |
| Bruto | 1,50 - 1,70 |
Esses valores servem como referência geral. Em solos turfosos, abundantes em resíduos vegetais, a densidade aparente pode ser tão baixa quanto 0,25 g / cm3, se for um solo mineral vulcânico fica em torno de 0,85 g / cm3, enquanto em solos muito compactados atinge 1,90 g / cm3.
O valor da densidade aparente também aumenta com a profundidade, uma vez que o solo geralmente é mais compactado e possui menor porcentagem de matéria orgânica..
O interior do terreno é composto por camadas ou estratos horizontais, chamados horizontes. Os horizontes têm diferentes texturas, composição e compactação. Portanto apresentam variação em termos de densidade aparente..
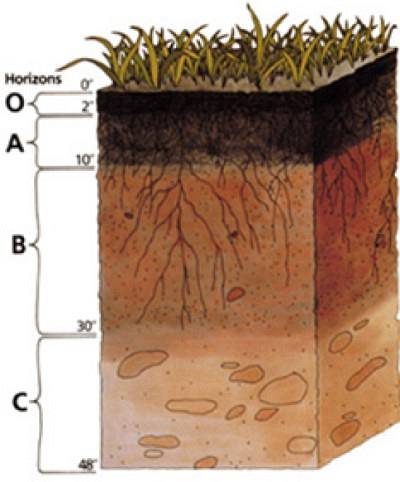
Um estudo de solo é baseado em seu perfil, que consiste em vários horizontes que ocorrem de forma vertical ordenada.
Uma vez que a variabilidade na densidade aparente é muito grande, muitas vezes tem que ser medida diretamente por vários procedimentos..
O método mais simples é extrair uma amostra do solo, inserindo nela uma broca com cilindro de metal espacial de volume conhecido e tomando cuidado para não compactar o solo. A amostra extraída é lacrada, para evitar perda de umidade ou alteração das características.
Em seguida, no laboratório a amostra é extraída, pesada e colocada em uma estufa a 105ºC para secar por 24 horas..
Embora seja a forma mais simples de se encontrar a densidade seca do solo, não é a mais recomendada para solos com texturas muito soltas ou cheios de pedras..
Para estes, o método de cavar um buraco e guardar a terra extraída é preferível, que será a amostra a secar. O volume da amostra é determinado despejando areia seca ou água no buraco cavado.
Em qualquer caso, a partir da amostra é possível determinar propriedades muito interessantes do solo para caracterizá-lo. O seguinte exercício resolvido descreve como fazê-lo.
Uma amostra de argila de 100 mm de comprimento é retirada do cilindro de amostra, cujo diâmetro interno também é de 100 mm. Quando pesada, obteve-se uma massa de 1531 g, que depois de seca foi reduzida para 1178 g. A gravidade específica das partículas é 2,75. É pedido para calcular:
a) A densidade aparente da amostra
b) Teor de umidade
c) O índice de vazios
d) Densidade seca
e) O grau de saturação
f) Conteúdo do ar
O volume sem alterar Vt é o volume original da amostra. Para um cilindro de diâmetro D e altura h, o volume é:
V cilindro = Vt = Área da base x altura = πDdois/ 4 = π x (100 x 10-3 m)dois x 100 x 10 -3 m / 4 = 0,000785 m3
A declaração afirma que a massa da amostra é Ms = 1531 g, portanto de acordo com a equação dada no início:
ρb = Ms / Vt = 1531 g / 0,000785 m3 = 1950 319 g / m3 = 1,95 Mg / m3
Uma vez que temos a massa original e a massa seca, a massa de água contida na amostra é a diferença entre as duas:
M Água = 1531 g - 1178 g = 353 g
A porcentagem de umidade na amostra é calculada da seguinte forma:
% Umidade = (Massa Água / Ms) x 100% = (353 g / 1178 g) = 29,97%
Para encontrar a razão de vazios, é necessário decompor o volume total da amostra Vt sobre:
V t = V partículas + Volume poros
O volume ocupado pelas partículas é obtido a partir da massa seca e do peso específico, dados obtidos no demonstrativo. A gravidade específica sg é o quociente entre a densidade do material e a densidade da água nas condições padrão, portanto, a densidade do material é:
ρ = sg x ρÁgua = 2,75 x 1 g / cm3 = 2,75 g / cm3
ρ = Ms / Vs → Vs = 1,178 g / 2,75 g / cm3 = 0,428 cm3 = 0,000428 m3
O volume de vazios na amostra é Vv = Vt - Vs = 0,000785 m3 - 0,000428 m3 = 0,000357 m3.
A proporção de vazios e isso é:
e = Vv / Vs = 0,000357 m3 / 0,000428 m3 = 0,83
A densidade seca da amostra é calculada conforme indicado na introdução:
ρs = Peso de elementos sólidos / Volume sólido + Volume poros= 1178 g / 0,000785 m3 = 1,5 Mg / m3
O grau de saturação é S = (VÁgua / Vv ) x 100%. Como sabemos a massa de água da amostra, calculada no item b) e sua densidade, o cálculo de seu volume é imediato:
ρÁgua = MÁgua / V Água → VÁgua = 353 g / 1 g / cm3 = 353 cm3 = 0,000353 m3
Por outro lado, o volume de vazios foi calculado no item c)
S = (0,000353 m3 / 0,000357 m3) x 100% = 98,9%
Finalmente, a porcentagem de conteúdo de ar é A = (Var / Vt) x 100%. O volume de ar corresponde a:
Vv - VÁgua = 0,000357 m3 - 0,000353 m3 = 0,000004 m3
A = (Var / Vt) x 100% = (0,000004 m3/ 0,000785 m3) x100% = 0,51%
For individuals who appreciate the art of sensuality and enjoy indulging in the satisfaction of lubricating their partner's skin with lotion, these galleries provide a plethora of scenes to fulfill your desires. Feast your eyes on high-quality, high-definition pictures of <a href="https://sexyhugetits.com/instagram-hoes-huge-tits-galleries-pics/">instagram hoes huge tits</a> and more. Delve into an environment of enticing material, featuring steamy occasions captured in pornographic picture galleries. And let's remember about the captivating women showcased here. From amateur models to seasoned porn stars, each one is fully exposed, allowing you to bask in the beauty of their enough bosoms and glistening nether areas. Dive into a assortment of XXX pictures which will leave you craving more, all designed for your viewing pleasure free. Enjoy the visual feast!