
Derivados sucessivos (com exercícios resolvidos)
As derivados sucessivos são as derivadas de uma função após a segunda derivada. O processo para calcular as derivadas sucessivas é o seguinte: temos uma função f, que podemos derivar e assim obter a função derivada f '. Podemos derivar esta derivada de f novamente, obtendo (f ')'.
Essa nova função é chamada de segunda derivada; todas as derivadas calculadas a partir da segunda são sucessivas; Estes, também chamados de ordem superior, têm grandes aplicações, como fornecer informações sobre o plot do gráfico de uma função, o teste da segunda derivada para extremos relativos e a determinação de séries infinitas..

Índice do artigo
- 1 definição
- 1.1 Exemplo 1
- 1.2 Exemplo 2
- 2 Velocidade e aceleração
- 2.1 Exemplo 1
- 2.2 Exemplo 2
- 3 aplicativos
- 3.1 Derivação implícita
- 3.2 Exemplo
- 3.3 Extremos relativos
- 3.4 Exemplo
- 3.5 série Taylor
- 3.6 Exemplo
- 4 referências
Definição
Usando a notação de Leibniz, temos que a derivada de uma função "y" com respeito a "x" é dy / dx. Para expressar a segunda derivada de "y" usando a notação de Leibniz, escrevemos o seguinte:

Em geral, podemos expressar derivadas sucessivas como segue com a notação de Leibniz, onde n representa a ordem da derivada.

Outras notações usadas são as seguintes:
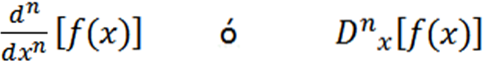
Alguns exemplos onde podemos ver as diferentes notações são:
Exemplo 1
Obtenha todas as derivadas da função f definida por:
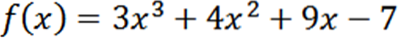
Usando as técnicas usuais de derivação, temos que a derivada de f é:

Repetindo o processo, podemos obter a segunda derivada, a terceira derivada e assim por diante.
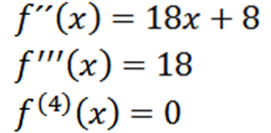
Observe que a quarta derivada é zero e a derivada de zero é zero, então temos:

Exemplo 2
Calcule a quarta derivada da seguinte função:
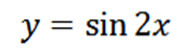
Derivando a função dada, temos como resultado:
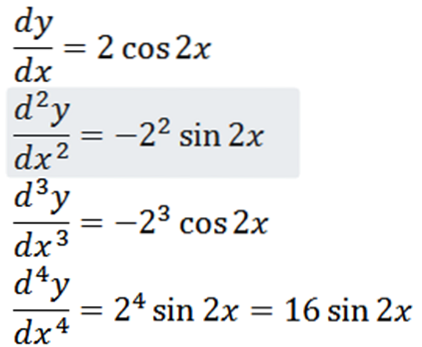
Velocidade e aceleração
Uma das motivações que levaram à descoberta da derivada foi a busca pela definição da velocidade instantânea. A definição formal é a seguinte:
Seja y = f (t) uma função cujo gráfico descreve a trajetória de uma partícula em um instante t, então sua velocidade em um instante t é dada por:

Uma vez obtida a velocidade de uma partícula, podemos calcular a aceleração instantânea, que é definida da seguinte forma:
A aceleração instantânea de uma partícula cujo caminho é dado por y = f (t) é:

Exemplo 1
Uma partícula se move ao longo de uma linha de acordo com a função de posição:

Onde "y" é medido em metros e "t" em segundos.
- Em que instante sua velocidade é 0?
- Em que instante é sua aceleração 0?
Ao derivar a função posição "y" temos que sua velocidade e aceleração são dadas respectivamente por:

Para responder à primeira questão, basta determinar quando a função v torna-se zero; isto é:
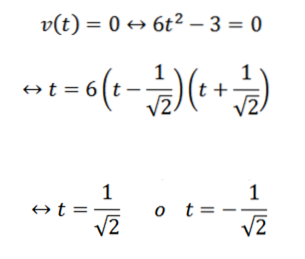
Prosseguimos com a seguinte questão de forma análoga:

Exemplo 2
Uma partícula se move ao longo de uma linha de acordo com a seguinte equação de movimento:

Determine "t, y" e "v" quando a = 0.
Saber que a velocidade e a aceleração são dadas por

Prosseguimos para derivar e obter:

Fazendo a = 0, temos:
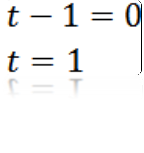
De onde podemos deduzir que o valor de t para que a seja igual a zero é t = 1.
Então, avaliando a função de posição e a função de velocidade em t = 1, temos:

Formulários
Derivação explícita
Derivadas sucessivas também podem ser obtidas por derivação implícita.
Exemplo
Dada a seguinte elipse, encontre “y”:

Derivando implicitamente em relação ax, temos:
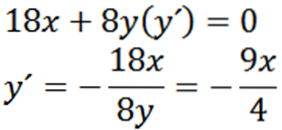
Então, re-derivar implicitamente em relação ax nos dá:

Finalmente, temos:
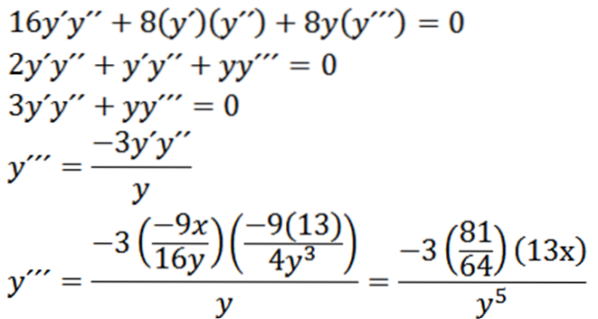
Extremos relativos
Outro uso que podemos dar às derivadas de segunda ordem é no cálculo de extremos relativos de uma função.
O critério da primeira derivada para extremos locais nos diz que, se temos uma função contínua f em um intervalo (a, b) e existe um c que pertence a dito intervalo tal que f 'desaparece em c (isto é, que c é um ponto crítico), um dos três casos pode ocorrer:
- Se f '(x)> 0 para qualquer x pertencente a (a, c) e f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
- Se f '(x) < 0 para cualquier x perteneciente a (a,c) y f'(x)>0 para x pertencente a (c, b), então f (c) é um mínimo local.
- Se f '(x) tem o mesmo sinal em (a, c) e em (c, b), isso implica que f (c) não é um extremo local.
Usando o critério da segunda derivada podemos saber se um número crítico de uma função é um máximo ou mínimo local, sem ter que ver qual é o sinal da função nos intervalos mencionados..
O segundo critério de deriva nos diz que se f '(c) = 0 e que f "(x) é contínuo em (a, b), acontece que se f" (c)> 0, então f (c) é um local mínimo e se f "(c) < 0 entonces f(c) es un máximo local.
Se f "(c) = 0, não podemos concluir nada.
Exemplo
Dada a função f (x) = x4 + (4/3) x3 - 4xdois, encontre os máximos e mínimos relativos de f aplicando o critério da segunda derivada.
Primeiro calculamos f '(x) e f "(x) e temos:
f '(x) = 4x3 + 4xdois - 8x
f "(x) = 12xdois + 8x - 8
Agora, f '(x) = 0 se, e somente se 4x (x + 2) (x - 1) = 0, e isso ocorre quando x = 0, x = 1 ou x = - 2.
Para determinar se os números críticos obtidos são extremos relativos, basta avaliar em f "e assim observar seu sinal..
f "(0) = - 8, então f (0) é um máximo local.
f "(1) = 12, então f (1) é um mínimo local.
f "(- 2) = 24, então f (- 2) é um mínimo local.
Série Taylor
Seja f uma função definida da seguinte forma:
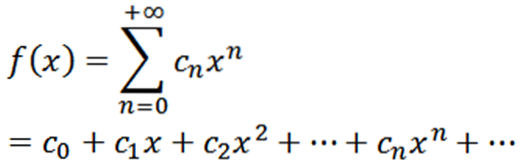
Esta função possui um raio de convergência R> 0 e derivadas de todas as ordens em (-R, R). As derivadas sucessivas de f nos dão:
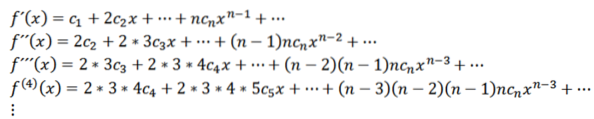
Tomando x = 0, podemos obter os valores de cn com base em seus derivados da seguinte forma:
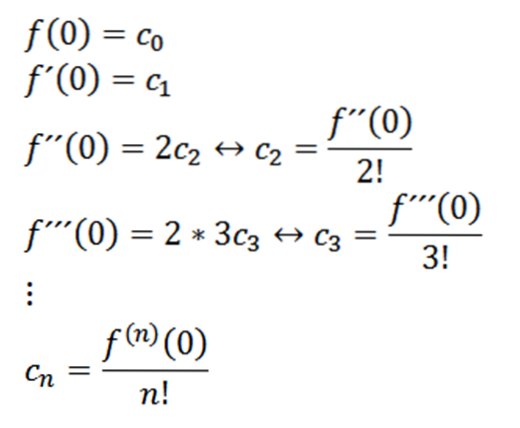
Se tomarmos n = 0 como a função f (ou seja, f ^ 0 = f), podemos reescrever a função da seguinte maneira:
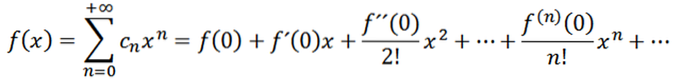
Agora vamos considerar a função como uma série de potências em x = a:
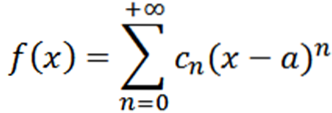
Se fizermos uma análise análoga à anterior, teríamos que escrever a função f como:
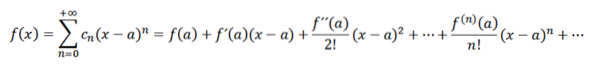
Essas séries são conhecidas como séries de Taylor de f a a. Quando a = 0, temos o caso particular denominado série Maclaurin. Este tipo de série é de grande importância matemática principalmente na análise numérica, pois graças a elas podemos definir funções em computadores como ex , sin (x) e cos (x).
Exemplo
Obtenha a série Maclaurin para ex.
Observe que se f (x) = ex, então f(n)(x) = ex e f(n)(0) = 1, então sua série Maclaurin é:
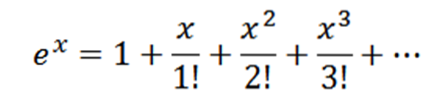
Referências
- Frank Ayres, J., & Mendelson, E. (s.f.). Cálculo 5ed. Mc Graw Hill.
- Leithold, L. (1992). O cálculo com geometria analítica. HARLA, S.A.
- Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Cálculo. México: Pearson Education.
- Saenz, J. (2005). Cálculo diferencial. Hipotenusa.
- Saenz, J. (s.f.). Cálculo integral. Hipotenusa.



Ainda sem comentários