
Demonstração da desigualdade do triângulo, exemplos, exercícios resolvidos
Se denomina desigualdade triangular à propriedade de dois números reais que consistem em que o valor absoluto de sua soma é sempre menor ou igual à soma de seus valores absolutos. Esta propriedade também é conhecida como desigualdade de Minkowski ou desigualdade triangular.
Essa propriedade dos números é chamada de desigualdade triangular porque nos triângulos acontece que o comprimento de um lado é sempre menor ou igual à soma dos outros dois, embora essa desigualdade nem sempre se aplique na área dos triângulos..

Existem várias provas da desigualdade triangular em números reais, mas neste caso vamos escolher uma com base nas propriedades de valor absoluto e do binômio ao quadrado..
Teorema: Para cada par de números para Y b em relação aos números reais, deve:
| a + b | ≤ | para | + | b |
Índice do artigo
- 1 demonstração
- 2 exemplos
- 2.1 Exemplo 1
- 2.2 Exemplo 2
- 2.3 Exemplo 3
- 2.4 Exemplo 4
- 2.5 Exemplo 5
- 2.6 Exemplo 6
- 3 exercícios resolvidos
- 3.1 Exercício 1
- 3.2 Exercício 2
- 3.3 Exercício 3
- 3.4 Exercício 4
- 4 referências
Demonstração
Começamos considerando o primeiro membro da desigualdade, que será elevado ao quadrado:
| a + b | ^ 2 = (a + b) ^ 2 = a ^ 2 + 2 a b + b ^ 2 (Eq. 1)
Na etapa anterior, utilizamos a propriedade de que qualquer número ao quadrado é igual ao valor absoluto desse número ao quadrado, ou seja: | x | ^ 2 = x ^ 2. O desenvolvimento do binômio quadrado também foi usado..
Todos os números x é menor ou igual ao seu valor absoluto. Se o número for positivo é igual, mas se o número for negativo será sempre menor que um número positivo. Neste caso o seu próprio valor absoluto, ou seja, pode-se afirmar que x ≤ | x |.
O produto (a b) é um número, portanto, aplica-se que (a b) ≤ | a b |. Quando esta propriedade é aplicada a (Eq. 1), temos:
| a + b | ^ 2 = a ^ 2 + 2 (a b) + b ^ 2 ≤ a ^ 2 + 2 | a b | + b ^ 2 (Eq. 2)
Tendo em conta que | a b | = | a || b | (Eq. 2) pode ser escrita da seguinte forma:
| a + b | ^ 2 ≤ a ^ 2 + 2 | a || b | + b ^ 2 (Eq. 3)
Mas, como dissemos antes que o quadrado de um número é igual ao valor absoluto do número ao quadrado, a equação 3 pode ser reescrita da seguinte forma:
| a + b | ^ 2 ≤ | a | ^ 2 + 2 | a | | b | + | b | ^ 2 (Eq. 4)
No segundo membro da desigualdade, um produto notável é reconhecido, que quando aplicado leva a:
| a + b | ^ 2 ≤ (| a | + | b |) ^ 2 (Eq. 5)
Na expressão anterior, deve-se observar que os valores a serem elevados ao quadrado em ambos os membros da desigualdade são positivos, portanto, também deve-se atender a que:
| a + b | ≤ (| a | + | b |) (Eq. 6)
A expressão acima é exatamente o que se queria demonstrar.
Exemplos
A seguir, vamos verificar a desigualdade triangular com vários exemplos.
Exemplo 1
Tomamos o valor a = 2 e o valor b = 5, ou seja, ambos os números positivos e verificamos se a desigualdade é satisfeita ou não.
| 2 + 5 | ≤ | 2 | + | 5 |
| 7 ≤ | 2 | + | 5 |
7 ≤ 2+ 5
A igualdade é verificada, portanto, o teorema da desigualdade do triângulo foi cumprido.
Exemplo 2
Os seguintes valores são escolhidos a = 2 eb = -5, ou seja, um número positivo e outro negativo, verificamos se a desigualdade é satisfeita ou não.
| 2 - 5 | ≤ | 2 | + | -5 |
| -3 | ≤ | 2 | + | -5 |
3 ≤ 2 + 5
A desigualdade é satisfeita, portanto, o teorema da desigualdade triangular foi verificado.
Exemplo 3
Tomamos o valor a = -2 e o valor b = 5, ou seja, um número negativo e outro positivo, verificamos se a desigualdade é satisfeita ou não.
| -2 + 5 | ≤ | -2 | + | 5 |
| 3 | ≤ | -2 | + | 5 |
3 ≤ 2 + 5
A desigualdade é verificada, portanto o teorema foi cumprido.
Exemplo 4
Os seguintes valores são escolhidos a = -2 eb = -5, ou seja, ambos os números negativos e verificamos se a desigualdade é satisfeita ou não.
| -2 - 5 | ≤ | -2 | + | -5 |
| -7 | ≤ | -2 | + | -5 |
7 ≤ 2+ 5
A igualdade é verificada, portanto, o teorema da desigualdade de Minkowski foi cumprido.
Exemplo 5
Tomamos o valor a = 0 e o valor b = 5, ou seja, um número zero e o outro positivo, então verificamos se a desigualdade é satisfeita ou não.
| 0 + 5 | ≤ | 0 | + | 5 |
| 5 ≤ | 0 | + | 5 |
5 ≤ 0+ 5
A igualdade é cumprida, portanto, o teorema da desigualdade do triângulo foi verificado.
Exemplo 6
Tomamos o valor a = 0 e o valor b = -7, ou seja, um número zero e o outro positivo, então verificamos se a desigualdade é satisfeita ou não.
| 0 - 7 | ≤ | 0 | + | -7 |
| -7 | ≤ | 0 | + | -7 |
7 ≤ 0+ 7
A igualdade é verificada, portanto, o teorema da desigualdade triangular foi cumprido.
Exercícios resolvidos
Nos exercícios a seguir, represente geometricamente a desigualdade do triângulo ou desigualdade de Minkowski para os números a e b.
O número a será representado como um segmento no eixo X, sua origem O coincide com o zero do eixo X e a outra extremidade do segmento (no ponto P) estará na direção positiva (à direita) do Eixo X se a> 0, mas se um < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.
Da mesma forma, o número b será representado como um segmento cuja origem está no ponto P. O outro extremo, ou seja, o ponto Q estará à direita de P se b for positivo (b> 0) e o ponto Q será | b | unidades à esquerda de P se b<0.
Exercício 1
Represente graficamente a desigualdade do triângulo para a = 5 e b = 3 | a + b | ≤ | para | + | b |, sendo c = a + b.
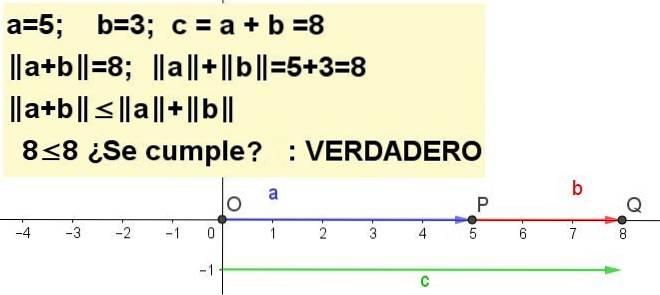
Exercício 2
Represente graficamente a desigualdade triangular para a = 5 e b = -3.
| a + b | ≤ | para | + | b |, sendo c = a + b.

Exercício 3
Mostre graficamente a desigualdade do triângulo para a = -5 e b = 3.
| a + b | ≤ | para | + | b |, sendo c = a + b.
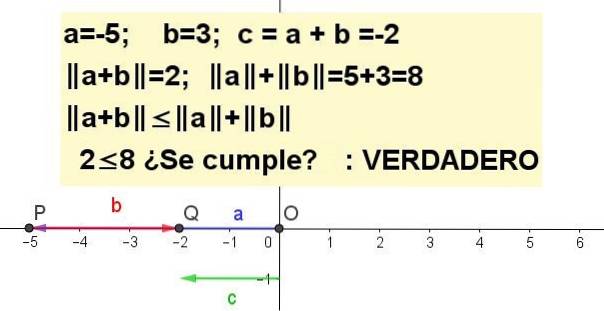
Exercício 4
Construa graficamente a desigualdade triangular para a = -5 e b = -3.
| a + b | ≤ | para | + | b |, sendo c = a + b.
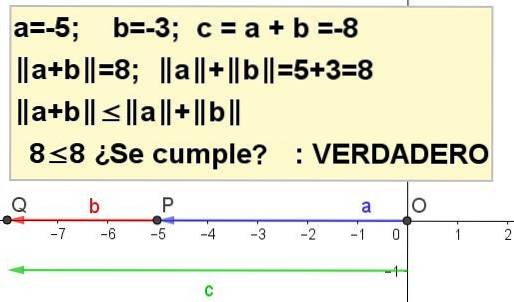
Referências
- E. Whitesitt. (1980) Boolean Algebra and its Applications. Empresa Editorial Continental C. A.
- Mícheál O 'Searcoid. (2003) Elements of Abstract Analysis… Departamento de matemática. Faculdade universitária Dublin, Beldfield, Dublind.
- J. Van Wyk. (2006) Matemática e Engenharia em Ciência da Computação. Instituto de Ciências e Tecnologia da Computação. National Bureau of Standards. Washington, D.C. 20234
- Eric Lehman. Matemática para Ciência da Computação. Google Inc.
- F. Thomson Leighton (1980). Cálculo. Departamento de Matemática e Ciência da Computação e Laboratório de IA, Instituto de Tecnologia de Massachusetts.
- Khan Academy. Teorema da Desigualdade do Triângulo. Recuperado de: khanacademy.org
- Wikipedia. Desigualdade triangular. Recuperado de: es. wikipedia.com


Ainda sem comentários