
Dilatação linear o que é, fórmula e coeficientes, exemplo
O dilatação linear ocorre quando um objeto experimenta expansão devido a uma variação na temperatura, predominantemente em uma dimensão. Isso se deve às características do material ou à sua forma geométrica..
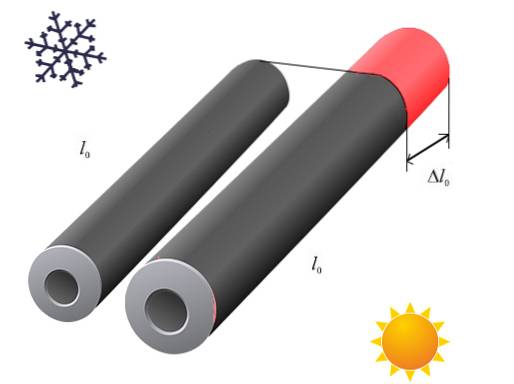
Por exemplo, em um fio ou barra, quando há aumento de temperatura, é o comprimento que sofre a maior alteração devido à dilatação térmica..

Os cabos nos quais as aves da figura anterior se empoleiram sofrem um estiramento quando sua temperatura aumenta; em vez disso, eles se contraem quando esfriam. O mesmo acontece, por exemplo, com as barras que formam os trilhos de uma ferrovia.
Índice do artigo
- 1 O que é dilatação linear?
- 2 Fórmula de dilatação linear e seu coeficiente
- 2.1 Coeficiente de expansão linear para vários materiais
- 3 exemplos trabalhados de expansão linear
- 3.1 Exemplo 1
- 3.2 Exemplo 2
- 3.3 Exemplo 3
- 3.4 Exemplo 4
- 4 referências
O que é dilatação linear?
Em um material sólido, os átomos mantêm suas posições relativas mais ou menos fixas em torno de um ponto de equilíbrio. No entanto, devido à agitação térmica, eles estão sempre oscilando em torno do mesmo.
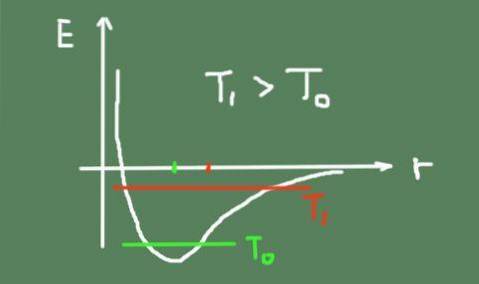
Conforme a temperatura aumenta, a oscilação térmica também aumenta, fazendo com que as posições de oscilação do meio mudem. Isso ocorre porque o potencial de ligação não é exatamente parabólico e tem assimetria em torno do mínimo.
Abaixo está uma figura que descreve a energia da ligação química em função da distância interatômica. Ele também mostra a energia total de oscilação em duas temperaturas, e como o centro de oscilação se move.
Fórmula de dilatação linear e seu coeficiente
Para medir a expansão linear, começamos com um comprimento inicial L e uma temperatura inicial T, do objeto cuja expansão será medida..
Suponha que este objeto seja uma barra cujo comprimento é L e as dimensões da seção transversal são muito menores que L.
Este objeto é primeiramente submetido a uma variação de temperatura ΔT, de forma que a temperatura final do objeto uma vez que o equilíbrio térmico com a fonte de calor tenha sido estabelecido será T '= T + ΔT.
Durante este processo, o comprimento do objeto também terá mudado para um novo valor L '= L + ΔL, onde ΔL é a variação do comprimento.
O coeficiente de expansão linear α é definido como o quociente entre a variação relativa do comprimento por unidade da variação da temperatura. A seguinte fórmula define o coeficiente de expansão linear α:
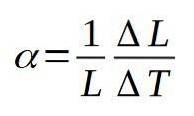
As dimensões do coeficiente de expansão linear são as do inverso da temperatura.
Coeficiente de expansão linear para vários materiais
A seguir, daremos uma lista do coeficiente de expansão linear para alguns materiais e elementos típicos. O coeficiente é calculado à pressão atmosférica normal com base em uma temperatura ambiente de 25 ° C; e seu valor é considerado constante em uma faixa ΔT de até 100 ° C.
A unidade do coeficiente de expansão linear será (° C)-1.
- Aço: α = 12 ∙ 10-6 (° C)-1
- Alumínio: α = 23 ∙ 10-6 (° C)-1
- Ouro: α = 14 ∙ 10-6 (° C)-1
- Cobre: α = 17 ∙ 10-6 (° C)-1
- Latão: α = 18 ∙ 10-6 (° C)-1
- Ferro: α = 12 ∙ 10-6 (° C)-1
- Vidro: α = (7 a 9) ∙ 10-6 (° C)-1
- Mercúrio: α = 60,4 ∙ 10-6 (° C)-1
- Quartzo: α = 0,4 ∙ 10-6 (° C)-1
- Diamante: α = 1,2 ∙ 10-6 (° C)-1
- Lead: α = 30 ∙ 10-6 (° C)-1
- Madeira de carvalho: α = 54 ∙ 10-6 (° C)-1
- PVC: α = 52 ∙ 10-6 (° C)-1
- Fibra de carbono: α = -0,8 ∙ 10-6 (° C)-1
- Betão: α = (8 a 12) ∙ 10-6 (° C)-1
A maioria dos materiais estica com o aumento da temperatura. No entanto, alguns materiais especiais, como a fibra de carbono, encolhem com o aumento da temperatura..
Exemplos trabalhados de dilatação linear
Exemplo 1
Um cabo de cobre é pendurado entre dois postes e seu comprimento em um dia frio a 20 ° C é de 12 m. Calcule o valor de sua longitude em um dia quente a 35 ° C.
Solução
Partindo da definição do coeficiente de expansão linear, e sabendo que para o cobre este coeficiente é igual a: α = 17 ∙ 10-6 (° C)-1
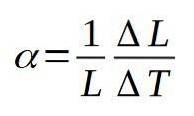
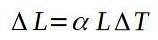
O comprimento do cabo de cobre aumenta, mas é de apenas 3 mm. Ou seja, o cabo passa de 12.000 m para 12.003 m.
Exemplo 2
Em uma ferraria, uma barra de alumínio sai da fornalha a 800 graus Celsius, medindo um comprimento de 10,00 m. Assim que esfriar para a temperatura ambiente de 18 graus Celsius, determine quanto tempo a barra terá.
Solução
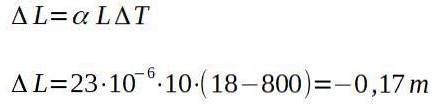
Em outras palavras, a barra, uma vez fria, terá um comprimento total de:
9,83 m.
Exemplo 3
Um rebite de aço tem um diâmetro de 0,915 cm. Em uma placa de alumínio é feito um furo de 0,910 cm. Estes são os diâmetros iniciais quando a temperatura ambiente é de 18 ° C.
A que temperatura mínima a placa deve ser aquecida para que o rebite passe pelo orifício? O objetivo disso é que quando o ferro voltar à temperatura ambiente, o rebite ficará bem encaixado na placa.
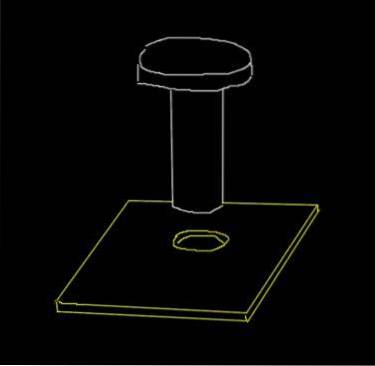
Solução
Embora a placa seja uma superfície, estamos interessados na dilatação do diâmetro do orifício, que é uma grandeza unidimensional..
Vamos chamar D0 ao diâmetro original da placa de alumínio, e D ao qual terá uma vez aquecido.
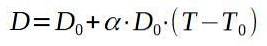
Resolvendo para a temperatura final T, temos:
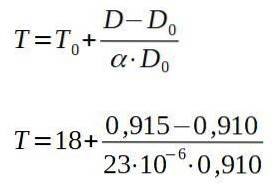
O resultado das operações anteriores é de 257 ° C, que é a temperatura mínima a que a placa deve ser aquecida para que o rebite passe pelo orifício.
Exemplo 4
O rebite e a placa do exercício anterior são colocados juntos em uma fornalha. Determine a temperatura mínima em que o forno deve estar para que o rebite de aço passe pelo orifício na placa de alumínio.
Solução
Nesse caso, tanto o rebite quanto o orifício ficarão dilatados. Mas o coeficiente de expansão do aço é α = 12 ∙ 10-6 (° C)-1, enquanto o do alumínio é α = 23 ∙ 10-6 (° C)-1 .
Em seguida, procuramos uma temperatura final T de modo que ambos os diâmetros coincidam.
Se chamarmos o rebite 1 e a placa de alumínio 2, procuramos uma temperatura final T tal que D1 = Ddois.
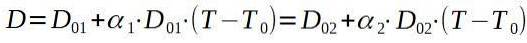
Se resolvermos para a temperatura final T, ficamos com:
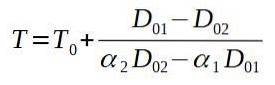
Então colocamos os valores correspondentes.
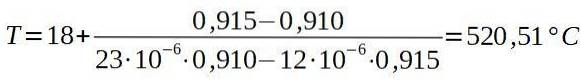
A conclusão é que o forno deve estar a pelo menos 520,5 ° C para que o rebite passe pelo orifício da placa de alumínio.
Referências
- Giancoli, D. 2006. Física: Princípios com Aplicações. Sexta Edição. Prentice Hall. 238-249.
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mac Graw Hill. 422-527.


Ainda sem comentários