O dilatação superficial É a expansão que ocorre quando um objeto experimenta variações em sua superfície devido a uma variação na temperatura. É devido às características do material ou à sua forma geométrica. A dilatação predomina em duas dimensões na mesma proporção.
Por exemplo, em uma folha, quando há uma mudança de temperatura, é a superfície da folha que sofre a maior alteração devido à expansão térmica..
A folha de metal da figura anterior aumenta sua largura e seu comprimento sensivelmente quando é aquecida pela radiação solar. Pelo contrário, ambos diminuem significativamente quando é resfriado devido à diminuição da temperatura ambiente..
É por essa razão que, quando os ladrilhos são instalados no piso, as bordas não devem ficar juntas, mas deve haver uma lacuna chamada junta de dilatação..
Além disso, este espaço é preenchido com uma mistura especial que possui um certo grau de flexibilidade, evitando que as placas rachem devido às fortes pressões que a dilatação térmica pode produzir..
Índice do artigo
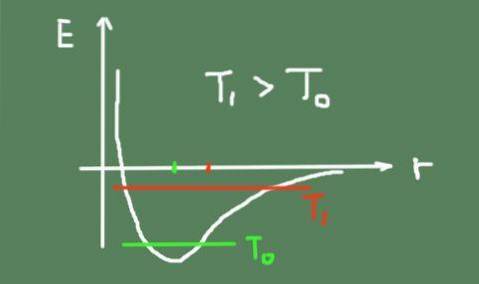
Em um material sólido, os átomos mantêm suas posições relativas mais ou menos fixas em torno de um ponto de equilíbrio. No entanto, devido à agitação térmica, eles estão sempre oscilando em torno do mesmo.
Conforme a temperatura aumenta, a oscilação térmica também aumenta, fazendo com que as posições de oscilação do meio mudem. Isso ocorre porque o potencial de ligação não é exatamente parabólico e tem assimetria em torno do mínimo.
Abaixo está uma figura que descreve a energia da ligação química em função da distância interatômica. A energia total de oscilação em duas temperaturas e como o centro de oscilação se move também são mostrados..
Para medir a dilatação da superfície, partimos de uma área inicial A e de uma temperatura inicial T, do objeto cuja dilatação será medida..
Suponha que o referido objeto seja uma folha de área A e sua espessura seja muito menor que a raiz quadrada da área A. A folha está sujeita a uma variação de temperatura ΔT, de modo que sua temperatura final uma vez que o equilíbrio térmico com a fonte de calor tenha sido estabelecido, será T '= T + ΔT.
Durante este processo térmico, a área de superfície também terá mudado para um novo valor A '= A + ΔA, onde ΔA é a mudança no comprimento. Assim, o coeficiente de expansão da superfície σ é definido como o quociente entre a variação relativa de área por unidade de variação de temperatura.
A fórmula a seguir define o coeficiente de expansão da superfície σ:
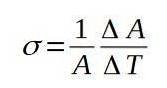
O coeficiente de expansão da superfície σ é praticamente constante em uma ampla faixa de valores de temperatura.
Pela definição de σ suas dimensões são inversas à temperatura. A unidade é geralmente ° C-1.
A seguir, daremos uma lista do coeficiente de expansão superficial para alguns materiais e elementos. O coeficiente é calculado na pressão atmosférica normal com base em uma temperatura ambiente de 25 ° C, e seu valor é considerado constante em uma faixa de ΔT de -10 ° C a 100 ° C.
A unidade do coeficiente de expansão da superfície será (° C)-1
- Aço: σ = 24 ∙ 10-6 (° C)-1
- Alumínio: σ = 46 ∙ 10-6 (° C)-1
- Ouro: σ = 28 ∙ 10-6 (° C)-1
- Cobre: σ = 34 ∙ 10-6 (° C)-1
- Latão: σ = 36 ∙ 10-6 (° C)-1
- Ferro: σ = 24 ∙ 10-6 (° C)-1
- Vidro: σ = (14 a 18) ∙ 10-6 (° C)-1
- Quartzo: σ = 0,8 ∙ 10-6 (° C)-1
- Diamante: σ = 2 ,, 4 ∙ 10-6 (° C)-1
- Lead: σ = 60 ∙ 10-6 (° C)-1
- Madeira de carvalho: σ = 108 ∙ 10-6 (° C)-1
- PVC: σ = 104 ∙ 10-6 (° C)-1
- Fibra de carbono: σ = -1,6 ∙ 10-6 (° C)-1
- Concreto: σ = (16 a 24) ∙ 10-6 (° C)-1
A maioria dos materiais estica com o aumento da temperatura. No entanto, alguns materiais, como a fibra de carbono, encolhem com o aumento da temperatura..
Uma placa de aço tem dimensões de 3m x 5m. De manhã e à sombra a temperatura é de 14 ° C, mas ao meio-dia o Sol a aquece até 52 ° C. Encontre a área final da placa.
Partimos da definição do coeficiente de expansão da superfície:
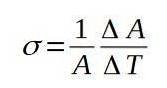
A partir daqui, resolvemos a variação na área:
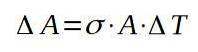
Em seguida, procedemos à substituição dos respectivos valores para encontrar o aumento da área pelo aumento da temperatura.
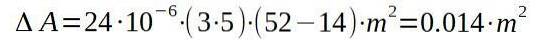
Ou seja, a área final será de 15.014 metros quadrados.
Mostre que o coeficiente de expansão da superfície é aproximadamente duas vezes o coeficiente de expansão linear.
Suponha que partamos de uma placa retangular com dimensões largura Lx e comprimento Ly, então sua área inicial será A = Lx ∙ Ly
Quando a placa sofre um aumento de temperatura ΔT, então suas dimensões também aumentam sendo sua nova largura Lx 'e seu novo comprimento Ly', de modo que sua nova área será A '= Lx' ∙ Ly '
A variação sofrida pela área da placa devido à mudança de temperatura será então
ΔA = Lx '∙ Ly' - Lx ∙ Ly
onde Lx '= Lx (1 + α ΔT) e Ly' = Ly (1 + α ΔT)
Ou seja, a mudança na área em função do coeficiente de expansão linear e a mudança na temperatura será:
ΔA = Lx (1 + α ΔT) ∙ Ly (1 + α ΔT) - Lx ∙ Ly
Isso pode ser reescrito como:
ΔA = Lx ∙ Ly ∙ (1 + α ΔT) ² - Lx ∙ Ly
Desenvolvendo o quadrado e multiplicando temos o seguinte:
ΔA = Lx ∙ Ly + 2α ΔT Lx ∙ Ly + (α ΔT) ² Lx ∙ Ly - Lx ∙ Ly
Uma vez que α é da ordem de 10-6, quando ao quadrado é da ordem de 10-12. Assim, o termo quadrático na expressão acima é desprezível.
Então, o aumento na área pode ser aproximado por:
ΔA ≈ 2α ΔT Lx ∙ Ly
Mas o aumento da área em função do coeficiente de expansão da superfície é:
ΔA = γ ΔT A
Da qual é derivada uma expressão que relaciona o coeficiente de expansão linear com o coeficiente de expansão da superfície.
γ ≈ 2 ∙ α
Ainda sem comentários