
Símbolos e fórmulas de diâmetro, como obtê-lo, circunferência
O diâmetro É a linha reta que passa pelo centro de uma curva plana fechada ou de uma figura em duas ou três dimensões e que também une seus pontos opostos. Normalmente é uma circunferência (uma curva plana), um círculo (uma figura plana), uma esfera ou um cilindro circular direito (objetos tridimensionais).
Embora circunferência e círculo sejam geralmente considerados sinônimos, há uma diferença entre os dois termos. A circunferência é a curva fechada que envolve o círculo, que atende à condição de que a distância entre qualquer um de seus pontos e o centro seja a mesma. Esta distância nada mais é do que o raio da circunferência. Em vez disso, o círculo é uma figura plana limitada pela circunferência.

No caso de circunferência, círculo e esfera, o diâmetro é um segmento reto que contém pelo menos três pontos: o centro mais dois pontos da borda da circunferência ou círculo, ou a superfície da esfera.
E quanto ao cilindro circular direito, o diâmetro se refere à seção transversal, que juntamente com a altura, são seus dois parâmetros característicos.
O diâmetro da circunferência e do círculo, simbolizado por ø ou simplesmente pela letra “D” ou “d”, está relacionado ao seu perímetro, contorno ou comprimento, que é denotado pela letra L:
L = π.D = π. ou
Enquanto houver uma circunferência, o quociente entre seu comprimento e seu diâmetro é o número irracional π = 3,14159 ..., desta forma:
π = L / D
Índice do artigo
- 1 Como obter o diâmetro?
- 1.1 Figuras de largura constante
- 2 diâmetro de um círculo
- 2.1 - Exemplo 1
- 2.2 - Exemplo 2
- 3 quantos diâmetros uma circunferência tem?
- 4 referências
Como obter o diâmetro?
Quando você tem o desenho da circunferência ou do círculo, ou diretamente do objeto circular, como uma moeda ou um anel por exemplo, é muito fácil encontrar o diâmetro com uma régua. Você só precisa ter certeza de que a borda da régua toca dois pontos da circunferência e o centro dela ao mesmo tempo..
Um paquímetro, vernier ou paquímetro é muito adequado para medir diâmetros externos e internos em moedas, aros, anéis, porcas, tubos e muito mais..

Se ao invés do objeto ou seu desenho houver dados como o raio R, então, multiplicando por 2, temos o diâmetro. E se o comprimento ou perímetro da circunferência for conhecido, o diâmetro também pode ser conhecido, limpando:
D = 2.R
D = L / π
Outra maneira de encontrar o diâmetro é conhecendo a área do círculo, a superfície esférica, a seção transversal do cilindro, a área curva do cilindro ou os volumes da esfera ou cilindro. Tudo depende de qual figura geométrica é. Por exemplo, o diâmetro está envolvido nas seguintes áreas e volumes:
-Área do círculo: π. (D / 2)dois
-Área de superfície esférica: 4π. (D / 2)dois
-Volume da esfera: (4/3) π. (D / 2)3
-Volume do cilindro circular direito: π. (D / 2)dois.H (H é a altura do cilindro)
Figuras de largura constante
O círculo é uma figura plana de largura constante, pois onde quer que você olhe para ele, a largura é o diâmetro D. No entanto, existem outras figuras talvez menos conhecidas cuja largura também é constante..
Vejamos primeiro o que se entende por largura de figura: é a distância entre duas linhas paralelas - linhas de suporte -, que por sua vez são perpendiculares à direção dada e que prendem a figura, como mostra a imagem à esquerda:
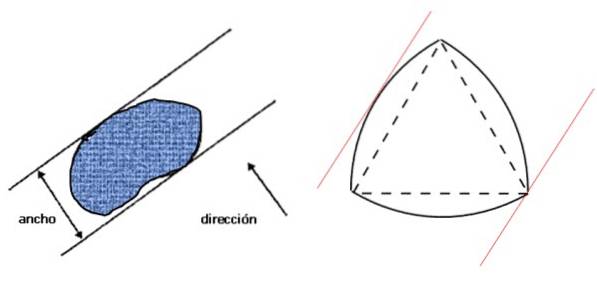
Próximo à direita está o triângulo de Reuleaux, que é uma figura de largura constante e que cumpre a condição especificada na figura à esquerda. Se a largura da figura for D, seu perímetro é dado pelo teorema de Barbier:
L = π.D
Os esgotos da cidade de São Francisco, na Califórnia, têm a forma de um triângulo de Reuleaux, batizado em homenagem ao engenheiro alemão Franz Reuleaux (1829 - 1905). Desta forma, as tampas não podem cair pelo buraco e menos material é usado para fazê-las, já que sua área é menor que a do círculo:
A = (1- √3) .πDdois = 0.705.Ddois
Enquanto para um círculo:
A = π. (D / 2)dois = (π / 4) Ddois= 0.785.Ddois
Mas este triângulo não é a única figura de largura constante. Você pode construir o chamado Polígonos Reuleaux com outros polígonos que têm um número ímpar de lados.
Diâmetro de uma circunferência

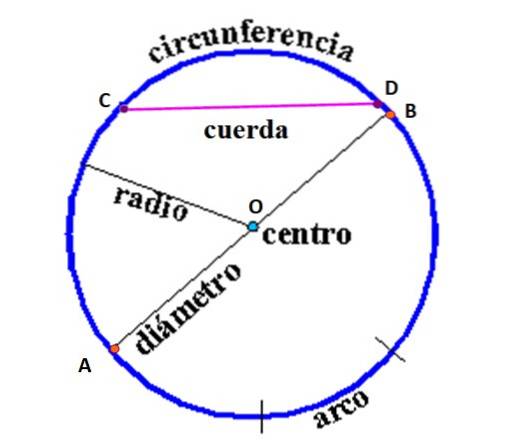
Na próxima figura estão os elementos da circunferência, definidos da seguinte forma:
Fragmento: segmento de reta que une dois pontos na circunferência. Na figura está o acorde que une os pontos C e D, mas podem ser desenhados infinitos acordes que unem qualquer par de pontos na circunferência.
Diâmetro: é o acorde que passa pelo centro, unindo dois pontos da circunferência com o centro O. É o acorde mais longo de uma circunferência, por isso é denominado "acorde maior".
Rádio: segmento de reta que une o centro a qualquer ponto da circunferência. Seu valor, como o diâmetro, é constante.
Circunferência: é o conjunto de todos os pontos equidistantes de O.
Arco: definido como um segmento de circunferência limitado por dois raios (não desenhado na figura).
- Exemplo 1
O retângulo mostrado tem 10 polegadas de altura, que quando enrolado forma um cilindro circular direito cujo diâmetro é de 5 polegadas. Responda as seguintes questões:
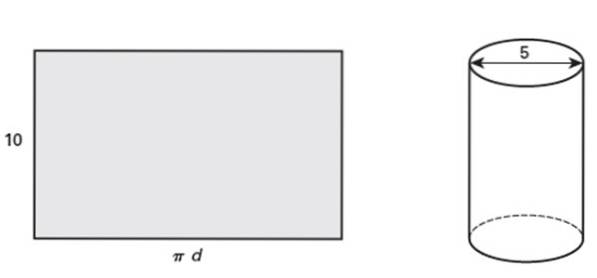
a) Qual é o contorno do tubo?
b) Encontre a área do retângulo
c) Calcule a área da seção transversal do cilindro.
Solução para
O contorno do tubo é L = π.D = 5π in = 15,71 in.
Solução b
A área do retângulo é base x altura, sendo a base L já calculada e a altura é de 10 polegadas conforme o enunciado, portanto:
A = 15,71 pol. X 10 pol. = 157,1 pol.dois.
Solução c
Finalmente, a área solicitada é calculada assim:
A = π. (D / 2)dois = (π / 4) Ddois = (π / 4) x (5 pol.)dois= 19,63 pol.dois.
- Exemplo 2
Calcule a área sombreada na Figura 5a. O quadrado tem o lado L.
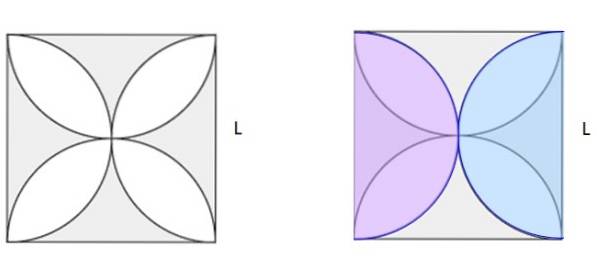
Solução
Na figura 5b, dois semicírculos de tamanho idêntico foram desenhados em rosa e azul, sobrepostos na figura original. Entre eles, eles formam um círculo completo. Se você encontrar a área do quadrado e subtrair a área do círculo, faça a área sombreada na Figura 5b. E olhando de perto, verifica-se que é metade da área sombreada em 5a.
-Área quadrada: Ldois
-Diâmetro do semicírculo: L
-Área do círculo: π. (L / 2)dois= (π / 4) Ldois
-Diferença de áreas = metade da área sombreada =
eudois - (π / 4) Ldois = [(4 - π) / 4] Ldois= 0,2146 Ldois
-Área sombreada = 2 x 0,2146 Ldois= 0,4292L2
Quantos diâmetros uma circunferência tem?
Diâmetros infinitos podem ser desenhados em uma circunferência, e qualquer um deles mede o mesmo.
Referências
- Antonio. Triângulos de Reuleaux e outras curvas de largura constante. Recuperado de: divulgators.com.
- Baldor, A. 2002. Plane and Space Geometry and Trigonometry. Grupo Cultural Pátria.
- Jiménez, R. Mathematics II. Geometria e trigonometria. 2ª Edição. Pearson.
- Wikipedia. Triângulo de Reuleaux. Recuperado de: es.wikipedia.org.
- Wolfram MathWorld. Diâmetro. Recuperado de: mathworld.wolfram.com.



Ainda sem comentários