
Fórmula de distribuição normal, características, exemplo, exercício

O distribuição normal ou distribuição Gaussiana é a distribuição de probabilidade em uma variável contínua, na qual a função de densidade de probabilidade é descrita por uma função exponencial de argumento quadrático e negativo, que dá origem a um formato de sino.
O nome de distribuição normal vem do fato de que essa distribuição é a que se aplica ao maior número de situações em que alguma variável aleatória contínua está envolvida em um determinado grupo ou população..
Exemplos onde a distribuição normal é aplicada são: a altura de homens ou mulheres, variações na medida de alguma magnitude física ou em traços psicológicos ou sociológicos mensuráveis, como o quociente intelectual ou os hábitos de consumo de um determinado produto.
Por outro lado, é chamada de distribuição gaussiana ou sino gaussiano, porque é esse gênio matemático alemão que é creditado com sua descoberta pelo uso que ele deu para descrever o erro estatístico de medições astronômicas no ano 1800..
No entanto, afirma-se que esta distribuição estatística foi publicada anteriormente por outro grande matemático de origem francesa, como Abraham de Moivre, no ano de 1733.
Índice do artigo
- 1 Fórmula
- 2 Características da distribuição normal
- 2.1 Intervalos de confiança
- 3 aplicações da distribuição normal
- 4 exemplo
- 5 Exercício resolvido
- 6 referências
Fórmula
Para a função de distribuição normal na variável contínua x, com parâmetros µ Y σ é denotado por:
N (x; μ, σ)
e é explicitamente escrito assim:
N (x; μ, σ) = ∫-∞x f (s; μ, σ) ds
Onde f (u; μ, σ) é a função de densidade de probabilidade:
f (s; μ, σ) = (1 / (σ√ (2π)) Exp (- sdois/ (2σdois))
A constante que multiplica a função exponencial na função de densidade de probabilidade é chamada de constante de normalização e foi escolhida de forma que:
N (+ ∞, μ, σ) = 1
A expressão anterior garante que a probabilidade de que a variável aleatória x está entre -∞ e + ∞ é 1, ou seja, 100% de probabilidade.
Parâmetro µ é a média aritmética da variável aleatória contínua x y σ o desvio padrão ou raiz quadrada da variância dessa mesma variável. No evento que μ = 0 Y σ = 1 temos então a distribuição normal padrão ou distribuição normal típica:
N (x; μ = 0, σ = 1)
Características da distribuição normal
1- Se uma variável estatística aleatória segue uma distribuição normal de densidade de probabilidade f (s; μ, σ), a maioria dos dados está agrupada em torno do valor médio µ e estão espalhados de tal forma que um pouco mais de ⅔ dos dados estão entre μ - σ Y μ + σ.
2- O desvio padrão σ é sempre positivo.
3- A forma da função densidade F assemelha-se a um sino, razão pela qual esta função é frequentemente chamada de sino gaussiano ou função gaussiana.
4- Em uma distribuição gaussiana a média, a mediana e a moda coincidem.
5- Os pontos de inflexão da função de densidade de probabilidade estão localizados precisamente em μ - σ Y μ + σ.
6- A função f é simétrica em relação a um eixo que passa por seu valor médio µ y tem assintoticamente zero para x ⟶ + ∞ e x ⟶ -∞.
7- Quanto maior o valor de σ maior dispersão, ruído ou distância dos dados em torno do valor médio. Ou seja, para maior σ o formato do sino é mais aberto. Em vez de σ pequeno indica que os dados estão apertados no meio e a forma do sino é mais fechada ou pontiaguda.
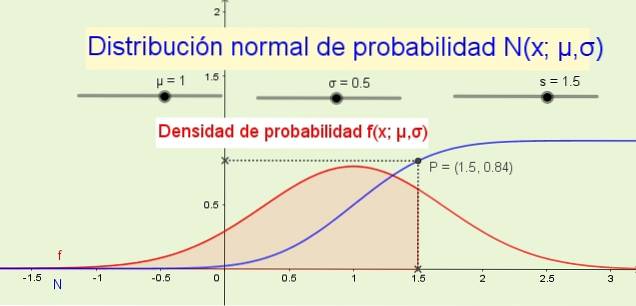
8- A função de distribuição N (x; μ, σ) indica a probabilidade de que a variável aleatória seja menor ou igual a x. Por exemplo, na Figura 1 (acima) a probabilidade P de que a variável x é menor ou igual a 1,5 é 84% e corresponde à área sob a função de densidade de probabilidade f (x; μ, σ) de -∞ a x.
Intervalos de confiança
9- Se os dados seguem uma distribuição normal, então 68,26% destes estão entre μ - σ Y μ + σ.
10-95,44% dos dados que seguem uma distribuição normal são encontrados entre μ - 2σ Y μ + 2σ.
11- 99,74% dos dados que seguem uma distribuição normal estão entre μ - 3σ Y μ + 3σ.
12- Se for uma variável aleatória x siga uma distribuição N (x; μ, σ), então a variável
z = (x - μ) / σ segue a distribuição normal padrão N (z, 0,1).
A mudança da variável x a z Chama-se padronização ou tipagem e é muito útil ao aplicar as tabelas da distribuição padrão aos dados que seguem uma distribuição normal não padrão..
Aplicações da distribuição normal
Para aplicar a distribuição normal é necessário passar pelo cálculo da integral da densidade de probabilidade, o que do ponto de vista analítico não é fácil e nem sempre existe um programa de computador que permita o seu cálculo numérico. Para tanto, são utilizadas as tabelas de valores normalizados ou padronizados, que nada mais é do que a distribuição normal no caso μ = 0 e σ = 1.
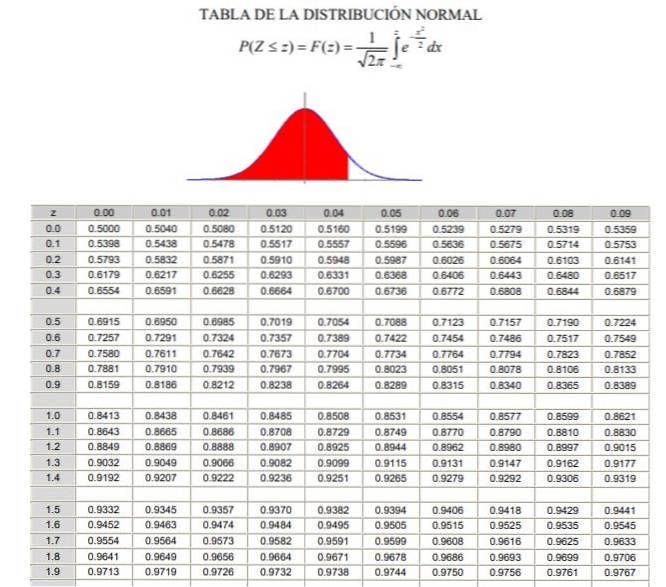
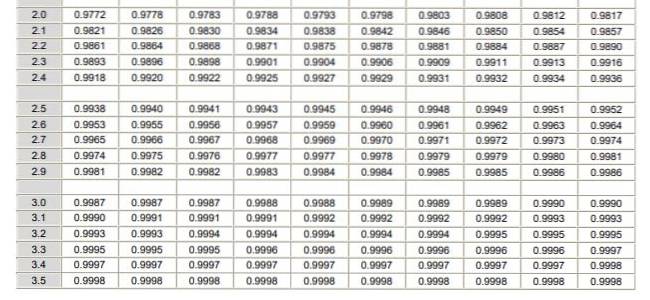
Deve-se observar que essas tabelas não incluem valores negativos. No entanto, usando as propriedades de simetria da função de densidade de probabilidade gaussiana, os valores correspondentes podem ser obtidos. No exercício resolvido mostrado abaixo, o uso da tabela nestes casos é indicado.
Exemplo
Suponha que você tenha um conjunto de dados aleatórios x que segue uma distribuição normal de média 10 e desvio padrão 2. Você deve encontrar a probabilidade de:
a) A variável aleatória x é menor ou igual a 8.
b) É menor ou igual a 10.
c) Que a variável x está abaixo de 12.
d) A probabilidade de que um valor x esteja entre 8 e 12.
Solução:
a) Para responder à primeira pergunta você simplesmente tem que calcular:
N (x; μ, σ)
Com x = 8, μ = 10 Y σ = 2. Percebemos que é uma integral que não possui solução analítica em funções elementares, mas a solução se expressa em função da função erro erf (x).
Por outro lado, existe a possibilidade de resolver a integral na forma numérica, que é o que muitas calculadoras, planilhas e programas de computador como o GeoGebra fazem. A figura a seguir mostra a solução numérica correspondente ao primeiro caso:
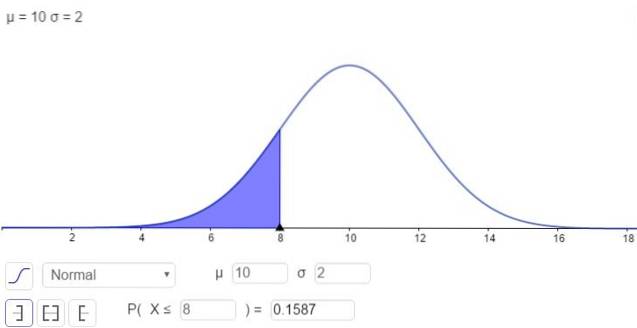
e a resposta é que a probabilidade de x estar abaixo de 8 é:
P (x ≤ 8) = N (x = 8; μ = 10, σ = 2) = 0,1587
b) Neste caso, procuramos encontrar a probabilidade de a variável aleatória x estar abaixo da média, que neste caso vale 10. A resposta não requer cálculo, pois sabemos que metade dos dados estão abaixo da média e a outra metade acima da média. Portanto, a resposta é:
P (x ≤ 10) = N (x = 10; μ = 10, σ = 2) = 0,5
c) Para responder a esta pergunta, você deve calcular N (x = 12; μ = 10, σ = 2), Isso pode ser feito com uma calculadora com funções estatísticas ou por meio de um software como o GeoGebra:
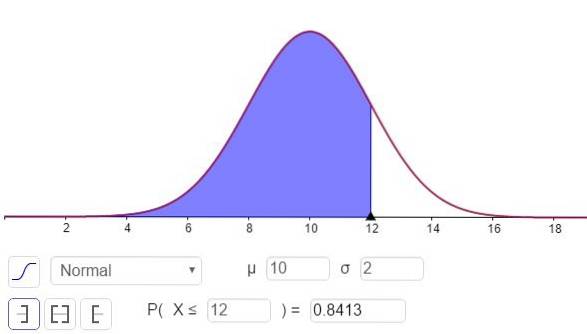
A resposta à parte c pode ser vista na figura 3 e é:
P (x ≤ 12) = N (x = 12; μ = 10, σ = 2) = 0,8413.
d) Para encontrar a probabilidade de que a variável aleatória x esteja entre 8 e 12, podemos usar os resultados das partes a e c da seguinte forma:
P (8 ≤ x ≤ 12) = P (x ≤ 12) - P (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26%.
Exercício resolvido
O preço médio das ações de uma empresa é de $ 25 com um desvio padrão de $ 4. Determine a probabilidade de:
a) Uma ação tem um custo inferior a $ 20.
b) Que tenha um custo superior a $ 30.
c) O preço está entre $ 20 e $ 30.
Use tabelas de distribuição normal padrão para encontrar respostas.
Solução:
Para fazer uso das tabelas, é necessário passar para a variável z normalizada ou digitada:
$ 20 na variável normalizada é igual a z = ($ 20 - $ 25) / $ 4 = -5/4 = -1,25 e
$ 30 na variável normalizada é igual a z = ($ 30 - $ 25) / $ 4 = +5/4 = +1,25.
a) $ 20 é igual a -1,25 na variável normalizada, mas a tabela não tem valores negativos, então colocamos o valor +1,25 que resulta no valor de 0,8944.
Se 0,5 for subtraído desse valor, o resultado será a área entre 0 e 1,25 que, a propósito, é idêntica (por simetria) à área entre -1,25 e 0. O resultado da subtração é 0,8944 - 0,5 = 0,3944 que é a área entre -1,25 e 0.
Mas a área de -∞ a -1,25 é de interesse, que será de 0,5 - 0,3944 = 0,1056. Conclui-se, portanto, que a probabilidade de um estoque estar abaixo de $ 20 é de 10,56%.
b) $ 30 na variável digitada z é 1,25. Para este valor, aparece na tabela o número 0,8944, que corresponde à área de -∞ a +1,25. A área entre +1,25 e + ∞ é (1 - 0,8944) = 0,1056. Ou seja, a probabilidade de que uma ação custe mais de $ 30 é de 10,56%.
c) A probabilidade de uma ação ter um custo entre $ 20 e $ 30 será calculada da seguinte forma:
100% -10,56% - 10,56% = 78,88%
Referências
- Estatística e probabilidade. Distribuição normal. Recuperado de: projectdescartes.org
- Geogebra. Geogebra clássica, cálculo de probabilidade. Recuperado de geogebra.org
- MathWorks. Distribuição gaussiana. Recuperado de: es.mathworks.com
- Mendenhall, W. 1981. Statistics for Management and Economics. 3º. edição. Grupo Editorial Iberoamérica.
- Stat Trek. Aprenda estatísticas a si mesmo. Distribuição de veneno. Recuperado de: stattrek.com,
- Triola, M. 2012. Estatísticas elementares. 11º. Ed. Pearson Education.
- Universidade de Vigo. Principais distribuições contínuas. Recuperado de: anapg.webs.uvigo.es
- Wikipedia. Distribuição normal. Recuperado de: es.wikipedia.org



Ainda sem comentários