
Características e exercícios das distribuições de probabilidade discreta
As distribuições de probabilidade discretas são uma função que atribui a cada elemento de X (S) = x1, x2,…, xi,…, onde X é uma dada variável aleatória discreta e S é o seu espaço amostral, a probabilidade de que tal evento ocorra. Esta função f de X (S) definida como f (xi) = P (X = xi) é às vezes chamada de função de massa de probabilidade.
Essa massa de probabilidades é geralmente representada em forma de tabela. Como X é uma variável aleatória discreta, X (S) tem um número finito de eventos ou infinito contável. Entre as distribuições de probabilidade discreta mais comuns, temos a distribuição uniforme, a distribuição binomial e a distribuição de Poisson..
Índice do artigo
- 1 recursos
- 2 tipos
- 2.1 Distribuição uniforme em n pontos
- 2.2 Distribuição binomial
- 2.3 Distribuição de Poisson
- 2.4 Distribuição hipergeométrica
- 3 exercícios resolvidos
- 3.1 Primeiro exercício
- 3.2 Segundo exercício
- 3.3 Terceiro exercício
- 3.4 Terceiro exercício
- 4 referências
Caracteristicas
A função de distribuição de probabilidade deve atender às seguintes condições:
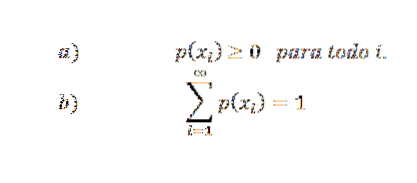
Além disso, se X assume apenas um número finito de valores (por exemplo x1, x2, ..., xn), então p (xi) = 0 se i> ny, portanto, a série infinita da condição b torna-se uma série finita.
Esta função também cumpre as seguintes propriedades:
Seja B um evento associado à variável aleatória X. Isso significa que B está contido em X (S). Especificamente, suponha que B = xi1, xi2,…. Portanto:
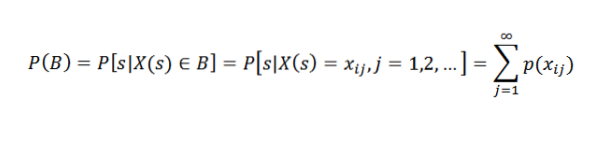
Em outras palavras: a probabilidade de um evento B é igual à soma das probabilidades dos resultados individuais associados a B.
Disto podemos concluir que se um < b, los sucesos (X ≤ a) y (a < X ≤ b) son mutuamente excluyentes y, además, su unión es el suceso (X ≤ b), por lo que tenemos:
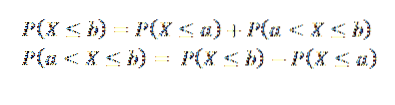
Tipos
Distribuição uniforme em n pontos
Diz-se que uma variável aleatória X segue uma distribuição caracterizada por ser uniforme em n pontos se a cada valor é atribuída a mesma probabilidade. Sua função de massa de probabilidade é:
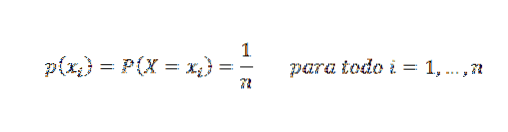
Suponha que temos um experimento que tem dois resultados possíveis, pode ser o lançamento de uma moeda cujos resultados possíveis são cara ou coroa, ou a escolha de um número inteiro cujo resultado pode ser um número par ou ímpar; este tipo de experimento é conhecido como testes de Bernoulli.
Em geral, os dois resultados possíveis são chamados de sucesso e fracasso, onde p é a probabilidade de sucesso e 1-p é a probabilidade de fracasso. Podemos determinar a probabilidade de x sucessos em n testes de Bernoulli que são independentes uns dos outros com a seguinte distribuição.
Distribuição binomial
É a função que representa a probabilidade de obtenção de x sucessos em n testes de Bernoulli independentes, cuja probabilidade de sucesso é p. Sua função de massa de probabilidade é:
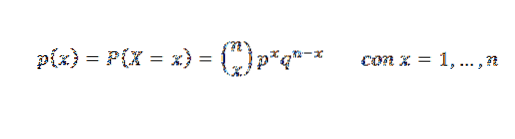
O gráfico a seguir representa a função de massa de probabilidade para diferentes valores dos parâmetros da distribuição binomial.
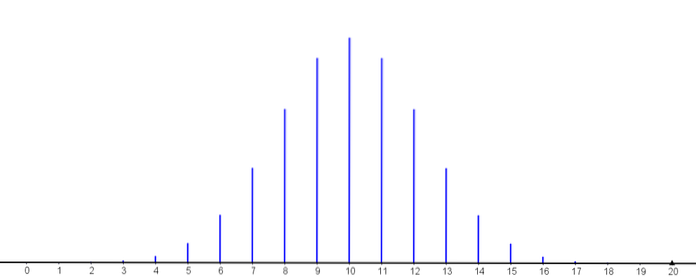
A seguinte distribuição deve seu nome ao matemático francês Simeon Poisson (1781-1840), que a obteve como o limite da distribuição binomial.
Distribuição de veneno
Diz-se que uma variável aleatória X tem uma distribuição de Poisson do parâmetro λ quando pode assumir os valores inteiros positivos 0,1,2,3, ... com a seguinte probabilidade:
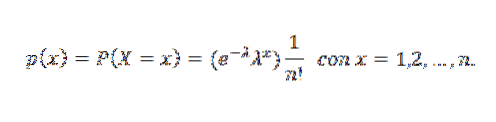
Nesta expressão λ é o número médio correspondente às ocorrências do evento para cada unidade de tempo, e x é o número de vezes que o evento ocorre.
Sua função de massa de probabilidade é:
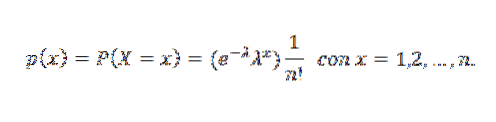
A seguir, um gráfico que representa a função de massa de probabilidade para diferentes valores dos parâmetros da distribuição de Poisson.
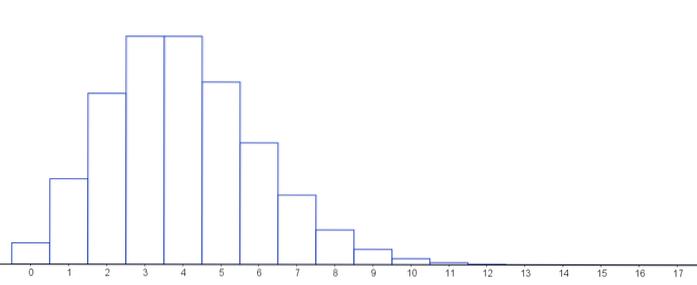
Observe que, desde que o número de sucessos seja baixo e o número de testes realizados em uma distribuição binomial seja alto, podemos sempre aproximar essas distribuições, pois a distribuição de Poisson é o limite da distribuição binomial.
A principal diferença entre essas duas distribuições é que, enquanto o binômio depende de dois parâmetros - a saber, n e p-, o Poisson depende apenas de λ, que às vezes é chamado de intensidade da distribuição..
Até agora, falamos apenas sobre distribuições de probabilidade para casos em que os diferentes experimentos são independentes uns dos outros; ou seja, quando o resultado de um não é afetado por algum outro resultado.
Quando ocorre o caso de haver experimentos não independentes, a distribuição hipergeométrica é muito útil..
Distribuição hipergeométrica
Seja N o número total de objetos de um conjunto finito, dos quais podemos identificar k deles de alguma forma, formando assim um subconjunto K, cujo complemento é formado pelos N-k elementos restantes.
Se escolhermos aleatoriamente n objetos, a variável aleatória X que representa o número de objetos pertencentes a K na dita escolha tem uma distribuição hipergeométrica dos parâmetros N, n e k. Sua função de massa de probabilidade é:
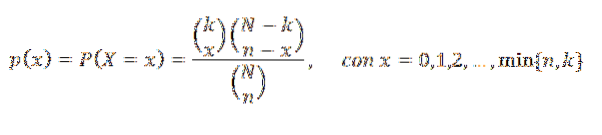
O gráfico a seguir representa a função de massa de probabilidade para diferentes valores dos parâmetros da distribuição hipergeométrica.
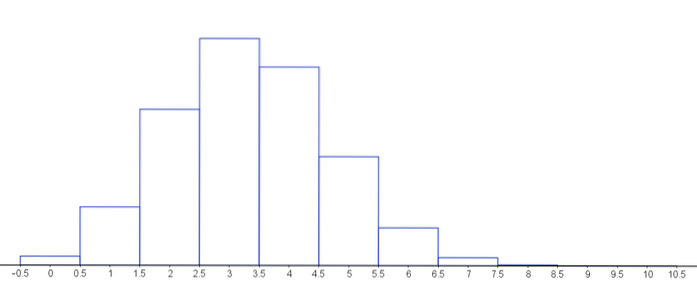
Exercícios resolvidos
Primeiro exercício
Suponha que a probabilidade de que um tubo de rádio (colocado em um determinado tipo de equipamento) opere por mais de 500 horas seja de 0,2. Se 20 tubos forem testados, qual é a probabilidade de que exatamente k deles funcionem por mais de 500 horas, k = 0, 1,2, ..., 20?
Solução
Se X for o número de tubos que funcionam mais de 500 horas, assumiremos que X tem uma distribuição binomial. Então
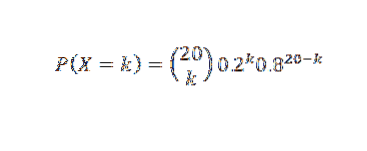
E assim:

Para k≥11, as probabilidades são menores que 0,001
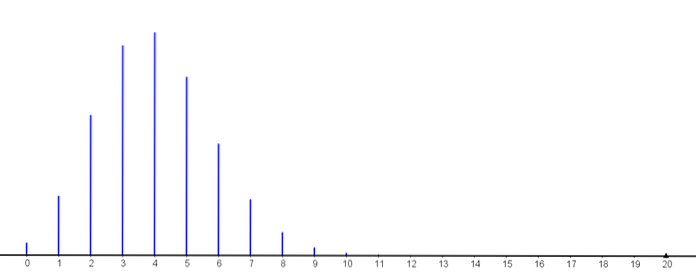
Assim, podemos observar como aumenta a probabilidade de que k destes funcionem por mais de 500 horas, até atingir seu valor máximo (com k = 4) e então começar a diminuir..
Segundo exercício
Uma moeda é lançada 6 vezes. Quando o resultado for caro, diremos que é um sucesso. Qual é a probabilidade de que duas cabeças apareçam exatamente?
Solução
Para este caso, temos n = 6 e ambas as probabilidades de sucesso e fracasso são p = q = 1/2
Portanto, a probabilidade de que duas cabeças sejam dadas (ou seja, k = 2) é
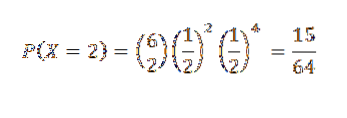
Terceiro exercício
Qual é a probabilidade de encontrar pelo menos quatro cabeças?
Solução
Para este caso, temos que k = 4, 5 ou 6
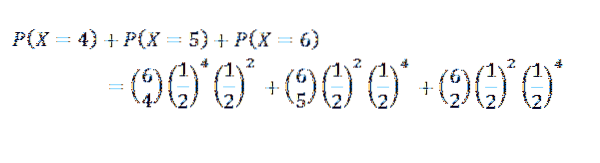
Terceiro exercício
Suponha que 2% dos itens produzidos em uma fábrica estejam com defeito. Encontre a probabilidade P de que haja três itens defeituosos em uma amostra de 100 itens.
Solução
Para este caso, poderíamos aplicar a distribuição binomial para n = 100 ep = 0,02 obtendo como resultado:
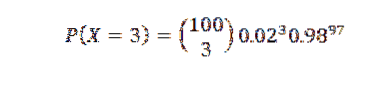
No entanto, como p é pequeno, usamos a aproximação de Poisson com λ = np = 2. A) Sim,
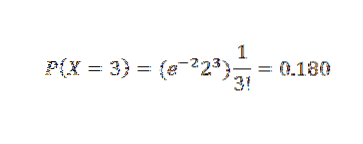
Referências
- Kai Lai Chung. Teoria de Proabilidade Elementar com Processos Estocásticos. Springer-Verlag New York Inc
- Kenneth.H. Rosen, Discrete Mathematics and its Applications. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Probabilidade e aplicações estatísticas. S.A. MEXICAN ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Solved Problems of Discrete Mathematics. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teoria e problemas de probabilidade. McGRAW-HILL.



Ainda sem comentários