Equação geral de uma linha cuja inclinação é igual a 2/3

A equação geral de uma linha L é a seguinte: Ax + By + C = 0, onde A, B e C são constantes, x é a variável independente ee a variável dependente.

A inclinação de uma linha, geralmente denotada pela letra m, que passa pelos pontos P = (x1, y1) e Q = (x0, y0) é o seguinte quociente m: = (y1-y0) / (x1 -x0 ).

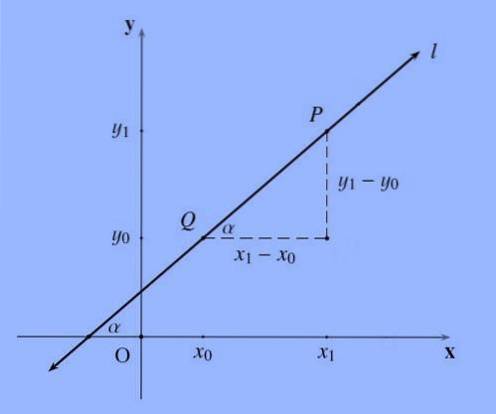
A inclinação de uma linha, representa de certa forma a inclinação; Mais formalmente, a inclinação de uma linha é a tangente do ângulo que ela forma com o eixo X..

Deve-se notar que a ordem em que os pontos são nomeados é indiferente, uma vez que (y0-y1) / (x0-x1) = - (y1-y0) / (- (x1-x0)) = (y1-y0) / (x1-x0).

Inclinação de uma linha

Se dois pontos são conhecidos pelos quais uma linha passa, é fácil calcular sua inclinação. Mas e se esses pontos não forem conhecidos?

Dada a equação geral de uma linha Ax + By + C = 0, sua inclinação é m = -A / B.

Qual é a equação geral de uma linha cuja inclinação é 2/3?

Como a inclinação da linha é 2/3, então a igualdade -A / B = 2/3 é estabelecida, com a qual podemos ver que A = -2 e B = 3. Portanto, a equação geral de uma linha com inclinação igual a 2/3 é -2x + 3y + C = 0.

Deve ser esclarecido que se A = 2 e B = -3 forem escolhidos, a mesma equação será obtida. Com efeito, 2x-3y + C = 0, que é igual ao anterior multiplicado por -1. O sinal de C não importa, pois é uma constante geral.

Outra observação que pode ser feita é que para A = -4 e B = 6 a mesma reta é obtida, embora sua equação geral seja diferente. Neste caso, a equação geral é -4x + 6y + C = 0.

Existem outras maneiras de encontrar a equação geral da linha?

A resposta é sim. Se a inclinação de uma linha é conhecida, existem duas maneiras, além da anterior, de encontrar a equação geral.

Para isso, são utilizadas a equação Ponto-Inclinação e a equação Shear-Inclinação..

-A equação Point-Slope: se m é a inclinação de uma reta e P = (x0, y0) um ponto através do qual ela passa, então a equação y-y0 = m (x-x0) é chamada de equação Point-Slope.

-A equação Shear-Slope: se m é a inclinação de uma linha e (0, b) é o corte da linha com o eixo Y, então a equação y = mx + b é chamada de equação Shear-Slope.

Usando o primeiro caso, obtém-se que a equação Ponto-Inclinação de uma reta cuja inclinação é 2/3 é dada pela expressão y-y0 = (2/3) (x-x0).

Para chegar à equação geral, multiplique por 3 em ambos os lados e todos os termos são agrupados em um lado da igualdade, com a qual se obtém que -2x + 3y + (2 × 0-3y0) = 0 é a equação geral da linha, onde C = 2 × 0-3y0.

Se o segundo caso for usado, obtém-se que a equação Cut-Slope de uma linha cuja inclinação é 2/3 é y = (2/3) x + b.

Novamente, multiplicando por 3 em ambos os lados e agrupando todas as variáveis, obtemos -2x + 3y-3b = 0. A última é a equação geral da linha onde C = -3b.

Na verdade, olhando atentamente para ambos os casos, pode-se ver que o segundo caso é simplesmente um caso particular do primeiro (quando x0 = 0).

Referências

1. Fleming, W., & Varberg, D. E. (1989). Matemática Pré-cálculo. Prentice Hall PTR.
2. Fleming, W., & Varberg, D. E. (1989). Matemática pré-cálculo: uma abordagem de resolução de problemas (2, edição ilustrada). Michigan: Prentice Hall.
3. Kishan, H. (2005). Cálculo integral. Editores e distribuidores da Atlantic.
4. Larson, R. (2010). Pré-cálculo (8 ed.). Cengage Learning.
5. Leal, J. M., & Viloria, N. G. (2005). Geometria Analítica Plano. Mérida - Venezuela: Editorial Venezolana C. A.
6. Pérez, C. D. (2006). Pré-cálculo. Pearson Education.
7. Saenz, J. (2005). Cálculo diferencial com funções transcendentes iniciais para ciência e engenharia (Segunda edição ed.). Hipotenusa.
8. Sullivan, M. (1997). Pré-cálculo. Pearson Education.