Fórmula de equações de segundo grau, como resolvê-los, exemplos, exercícios

As equações quadráticas ou quadráticas e um desconhecido tem a forma machado^dois + bx + c = 0. Onde a ≠ 0, já que se fosse 0, a equação seria transformada em uma equação linear, e os coeficientes a, b e c são números reais.

A incógnita a ser determinada é o valor de x. Por exemplo, a equação 3x^dois - 5x + 2 = 0 é uma equação quadrática completa.

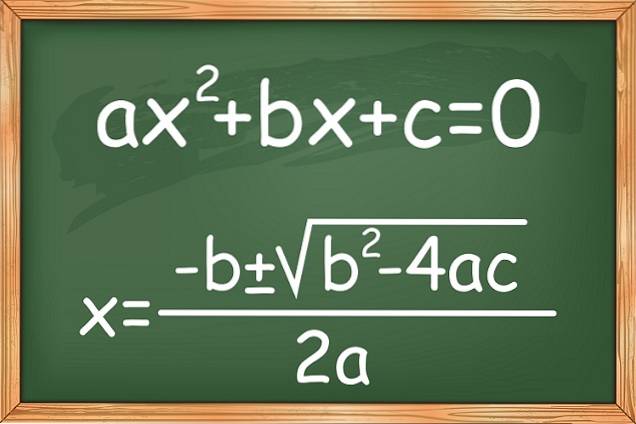
Existem também variantes que são conhecidas como equações de segundo grau incompletas, que não possuem nenhum dos termos, exceto o de machado^dois. aqui estão alguns exemplos:

x^dois - 25 = 0

3x^dois - 5x = 0

Al Juarismi, o famoso matemático árabe da antiguidade, descreveu em suas obras vários tipos de equações de primeiro e segundo grau, mas apenas com coeficientes positivos. No entanto, foi o matemático francês François Viete quem primeiro introduziu as letras para simbolizar as quantidades e propor a solução por meio da fórmula resoluto:

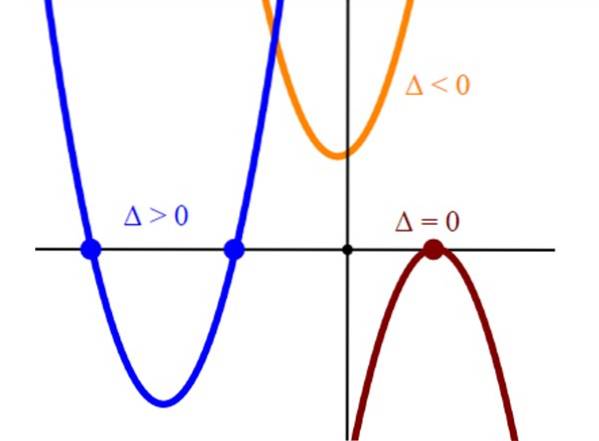
Esta é uma fórmula geral que permite resolver uma equação quadrática, encontrando suas raízes ou zeros, mesmo que as soluções não sejam reais. Existem também outras maneiras de resolvê-los.

Índice do artigo

• 1 Como resolver equações quadráticas?
  • 1.1 Resolução por fatoração
  • 1.2 Método gráfico
  • 1.3 Resolução com calculadora científica
  • 1.4 Discriminante de uma equação quadrática
• 2 Exemplos de equações quadráticas simples
  • 2.1 Equação da forma x2 + mx + n = 0
  • 2.2 Equação incompleta da forma ax2 + c = 0
  • 2.3 Equação incompleta da forma ax2 + bx = 0
  • 2.4 Equações com denominador
  • 2.5 Equações de ordem superior que se tornam quadráticas
• 3 exercícios resolvidos simples
  • 3.1 - Exercício 1
  • 3.2 - Exercício 2
  • 3.3 - Exercício 3
• 4 referências

Como resolver equações quadráticas?

Equações de segundo grau podem ser resolvidas pela fórmula dada acima, e também existem outros procedimentos algébricos que podem dar resultado em algumas equações.

Vamos resolver a equação proposta no início com a fórmula, um método válido para qualquer equação quadrática com uma incógnita:

3x^dois - 5x + 2 = 0

Para usar a fórmula corretamente, observamos que:

• para é o coeficiente do termo com x^dois
• b é o coeficiente do termo linear
• c é o termo independente.

Vamos identificá-los a partir da mesma equação:

a = 3

b = -5

c = 2

Observe que o sinal que acompanha o coeficiente deve ser levado em consideração. Agora, substituímos esses valores na fórmula:

No numerador existe o símbolo “mais - menos” ±, que indica que a quantidade com raiz pode ser considerada positiva e também negativa. Uma equação quadrática tem no máximo duas soluções reais, e este símbolo leva isso em consideração.

Vamos chamar x₁ e x_dois a essas duas soluções, então:

x₁ = (5 + 1) / 6 = 1

x_dois = (5-1) / 6 = 4/6 = 2/3

Resolução por fatoração

Algumas equações do segundo grau consistem em trinômios que são facilmente fatorados. Nesse caso, esse método é muito mais rápido. Vamos considerar a equação:

x^dois + 7x - 18 = 0

A fatoração tem a seguinte forma:

(x +) ⋅ (x -)

Os espaços em branco são preenchidos com dois números que, quando multiplicados, dão 18 e, quando subtraídos, dão 7. Os sinais entre parênteses são escolhidos com este critério:

-No primeiro parêntese, o sinal é colocado entre o primeiro e o segundo termo.

-E no segundo parêntese está o produto dos sinais que são vistos.

Já os números são facilmente pontuados neste caso: são 9 e 2. O maior é sempre colocado no primeiro dos parênteses, assim:

x^dois + 7x - 18 = (x + 9). (x - 2)

O leitor pode verificar por meio da propriedade distributiva, que ao desenvolver o produto do lado direito da igualdade é obtido o trinômio da esquerda. Agora a equação foi reescrita:

(x + 9) ⋅ (x - 2) = 0

Para que a igualdade seja cumprida, basta que um dos dois fatores seja zero. Então, no primeiro você tem que fazer x₁ = -9 ou pode ser que o segundo fator desapareça, caso em que x_dois = 2. Estas são as soluções da equação.

Método gráfico

As raízes ou soluções da equação quadrática correspondem às interseções da parábola y = machado^dois + bx + c com o eixo horizontal ou eixo x. Assim, ao representar graficamente a parábola correspondente, encontraremos a solução da equação quadrática fazendo y = 0.

Os cortes das parábolas com o eixo horizontal representam as soluções da equação machado^dois + bx + c = 0. Uma parábola que apenas corta o eixo horizontal em um único ponto tem uma única raiz e este sempre será o vértice da parábola.

E, finalmente, se uma parábola não corta o eixo horizontal, a equação correspondente machado^dois + bx + c = 0 falta soluções reais.

Construir um gráfico manualmente pode ser trabalhoso, mas com o uso de programas que fazem gráficos online é muito simples.

Resolução com calculadora científica

Muitos modelos de calculadoras científicas têm a opção de resolver equações quadráticas (e também outros tipos de equações). Para descobrir, você tem que verificar o menu.

Uma vez que a equação quadrática de uma opção desconhecida é escolhida, o menu pede para inserir os valores dos coeficientes a, bec e retorna as soluções reais se eles existirem. E também existem modelos de calculadoras científicas que trabalham com números complexos e oferecem essas soluções.

Discriminante de uma equação quadrática

Para saber se a equação tem soluções reais ou não, e quantas existem, sem ter que resolver primeiro, o discriminante Δ é definido como a quantidade sob a raiz quadrada:

Δ = b^dois - 4ac

De acordo com o sinal do discriminante, sabe-se quantas soluções a equação possui de acordo com este critério:

-Duas soluções reais: Δ> 0

-Uma solução real (ou duas soluções idênticas): Δ = 0

-Nenhuma solução real: Δ  < 0

Por exemplo, quantas soluções a equação quadrática -7x^dois +12x + 64 = 0? Identificamos os coeficientes:

a = -7

b = 12

c = 64

Δ = b^dois - 4ac = 12^dois - 4x (-7) x 64 = 144 + 1792 = 1936> 0

A equação tem duas soluções. Agora vamos ver este outro:

x^dois - 6x + 9 = 0

a = 1

b = -6

c = 9

Δ = (-6)^dois - 4 x 1 x 9 = 36 - 36 = 0

Esta é uma equação com uma única solução ou com duas soluções iguais.

Exemplos de equações quadráticas simples

No início dissemos que as equações do segundo grau poderiam ser completas se o trinômio fosse, e incompletas se o termo linear ou independente estivesse faltando. Agora, vamos examinar alguns tipos específicos:

Equação da forma x^dois + mx + n = 0

Neste caso, a = 1 e a fórmula se reduz a:

Para este tipo de equação, e sempre dependendo dos demais coeficientes, o método de fatoração pode funcionar bem, como vimos na seção anterior.

Equação incompleta da forma machado^dois + c = 0

A solução, se existir, é na forma:

Existe uma solução real quando a ou c têm sinal negativo, mas se os dois termos têm o mesmo sinal, a solução será imaginária.

Equação incompleta da forma machado^dois + bx = 0

Essa equação é resolvida rapidamente por meio de fatoração, uma vez que x é um fator comum em ambos os termos. Uma das soluções é sempre x = 0, a outra é encontrada assim:

machado^dois + bx = 0

x (ax + b) = 0

ax + b = 0 → x = -b / a

Vamos ver um exemplo abaixo. Separar:

x^dois - 5x = 0

x (x - 5) = 0

Portanto x₁ = 0 e x_dois = 5

Equações com denominador

Existem várias equações de tipo racional, em que o desconhecido pode estar presente tanto no numerador como no denominador, ou mesmo apenas neste último, e que por meio de manipulações algébricas se reduzem a equações quadráticas..

A maneira de resolvê-los é multiplicar ambos os lados da igualdade pelo mínimo múltiplo comum ou m.c.m dos denominadores e, em seguida, reorganizar os termos. Por exemplo:

Equações de ordem superior que se tornam quadráticas

Existem equações de ordem superior que podem ser resolvidas como se fossem quadráticas por meio de uma mudança de variável, por exemplo esta equação bi-quadrado:

x⁴ - 10x^dois + 9 = 0

Deixe x^dois = u, então a equação se torna:

ou^dois - 10u + 9 = 0

Esta equação é resolvida rapidamente pela fatoração, encontrando dois números que se multiplicam por 9 e somam 10. Esses números são 9 e 1:

(u - 9). (u - 1) = 0

Portanto, as soluções desta equação são u₁ = 9 e u_dois = 1. Agora retornamos a mudança:

x^dois = 9 → x₁ = 3 e x_dois = -3

x^dois = 1 → x₁ = 1 e x_dois = -1

A equação original é de ordem 4, portanto tem pelo menos 4 raízes. O do exemplo é -3, -1, 1 e 3.

Exercícios resolvidos simples

- Exercício 1

Resolva a seguinte equação quadrática com a incógnita no denominador:

O mínimo múltiplo comum é x (x + 2) e você deve multiplicar todos os termos:

A expressão equivalente permanece:

5x (x + 2) - x = x (x + 2)

Nós desenvolvemos:

5x^dois + 10x - x = x^dois + 2x

Todos os termos são transpostos para a esquerda da igualdade e para a direita deixamos 0:

5x^dois + 10x - x - x^dois - 2x = 0

4x^dois - 7x = 0

Nós fatoramos, uma vez que é uma equação incompleta:

x (4x - 7) = 0

Uma das soluções é x = 0, a outra é:

4x = 7

x = 7/4

- Exercício 2

Encontre a solução das equações quadráticas:

a) -7x^dois +12x + 64 = 0

b) x^dois - 6x + 9 = 0

Solução para

Desta equação conhecemos o determinante Δ, porque foi calculado como exemplo antes, então vamos tirar proveito disso, expressando a fórmula de resolução assim:

x₁ = (-12 + 44) / -14 = - (32/14) = - (16/7)

x_dois = (-12 - 44) / -14 = 4

Solução b

O trinômio quadrado x^dois - 6x + 9 é fatorável, uma vez que é um trinômio quadrado perfeito:

x^dois - 6x + 9 = (x-3)^dois = 0

A solução para esta equação é x = 3.

- Exercício 3

Qual é a equação cujas soluções são 3 e 4?

Solução

A expressão fatorada é:

(x - 3) ⋅ (x - 4) = 0

Aplicando propriedade distributiva:

x^dois - 4x -3x + 12 = 0

Os dois termos centrais são semelhantes e podem ser reduzidos, restando:

x^dois - 7x + 12 = 0

Referências

1. Baldor. 1977. Elementary Algebra. Edições Culturais Venezuelanas.
2. Hoffman, J. Selection of Mathematics Topics. Volume 2.
3. Jiménez, R. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Pré-cálculo: Matemática para Cálculo. 5 ª. Edição. Cengage Learning.
5. Zapata, F. 4 maneiras de resolver uma equação quadrática. Recuperado de: francesphysics.blogspot.com.
6. Zill, D. 1984. Algebra and Trigonometry. Colina Mcgraw.