
Fórmulas de energia gravitacional, características, aplicações, exercícios
O energia gravitacional É aquele que um objeto massivo possui quando está imerso no campo gravitacional produzido por outro. Alguns exemplos de objetos com energia gravitacional são: a maçã na árvore, a maçã que cai, a Lua orbitando a Terra e a Terra orbitando o Sol.
Isaac Newton (1642-1727) foi o primeiro a perceber que a gravidade é um fenômeno universal e que todo objeto com massa em seu ambiente produz um campo capaz de produzir uma força sobre outro.

Índice do artigo
- 1 Fórmulas e equações
- 2 Características da energia gravitacional
- 2.1 Campo gravitacional e potencial
- 3 aplicativos
- 3.1 Potencial gravitacional da Terra
- 3.2 Energia potencial perto da superfície da terra
- 4 exercícios
- 4.1 Exercício 1: colapso gravitacional da Terra
- 4.2 Exercício 2: Colapso gravitacional e velocidade de escape
- 4.3 Exercício 3: Energia gravitacional da maçã
- 5 referências
Fórmulas e equações
A força a que Newton se referia é conhecida como força gravitacional e fornece energia ao objeto sobre o qual atua. Newton formulou a lei da gravitação universal da seguinte forma:
"Sejam dois objetos pontuais de massas m1 e m2 respectivamente, cada um exerce uma força atrativa sobre o outro que é proporcional ao produto de suas massas e inversamente proporcional ao quadrado da distância que os separa".
Energia gravitacional OU associado à força gravitacional F isso é:

Um objeto que está imerso em um campo gravitacional possui energia potencial gravitacional OU e energia cinética K. Se não houver outras interações, ou se forem de intensidade desprezível, a energia total E do referido objeto é a soma de sua energia gravitacional mais sua energia cinética:
E = K + U
Se um objeto está em um campo gravitacional e nenhuma outra força dissipativa está presente, como atrito ou resistência do ar, então a energia total E é uma quantidade que permanece constante durante o movimento.
Características da energia gravitacional
- Um objeto tem energia potencial gravitacional se estiver apenas na presença do campo gravitacional produzido por outro.
- A energia gravitacional entre dois objetos aumenta à medida que a distância de separação entre eles é maior.
- O trabalho realizado pela força gravitacional é igual e contrário à variação da energia gravitacional da posição final em relação à sua posição inicial..
- Se um corpo está sujeito apenas à ação da gravidade, a variação de sua energia gravitacional é igual e contrária à variação de sua energia cinética..
- A energia potencial de um objeto de massa m que está em uma altura h com relação à superfície da terra é mgh vezes maior do que a energia potencial na superfície, sendo g a aceleração da gravidade, para alturas h muito menor que o raio terrestre.
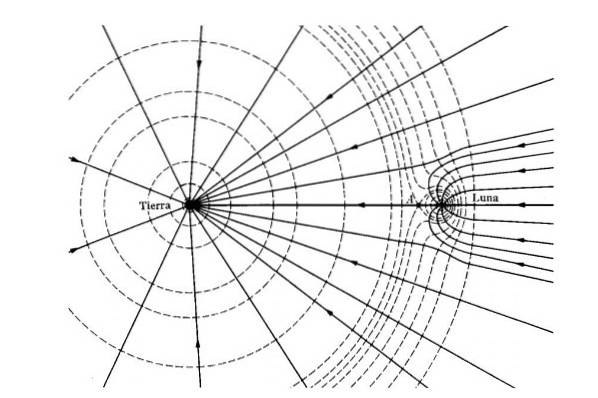
Campo gravitacional e potencial
O campo gravitacional g é definido como a força gravitacional F por unidade de massa. É determinado colocando uma partícula de teste m em cada ponto no espaço e calculando o quociente entre a força que atua sobre a partícula de teste dividido pelo valor de sua massa:
g = F / m
O potencial gravitacional V de um objeto de massa m é definido como a energia potencial gravitacional desse objeto dividido por sua própria massa.
A vantagem desta definição é que o potencial gravitacional depende apenas do campo gravitacional, de forma que uma vez que o potencial é conhecido V, energia gravitacional OU de um objeto de massa m isso é:
U = m.V

Formulários
A energia potencial gravitacional é aquela armazenada pelos corpos quando eles estão em um campo gravitacional.
Por exemplo, a água contida em um tanque tem mais energia à medida que o tanque é mais alto..
Quanto maior for a altura do tanque, maior será a velocidade da água que sai da torneira. Isso se deve ao fato de que a energia potencial da água na altura do tanque é transformada em energia cinética da água na saída da torneira..
Quando a água é represada no topo de uma montanha, essa energia potencial pode ser aproveitada para girar as turbinas de geração de energia..
A energia gravitacional também explica as marés. Como a energia e a força gravitacional dependem da distância, a atração gravitacional da Lua é maior na face da Terra mais próxima da Lua do que na face mais distante e oposta..
Isso produz uma diferença de forças que deforma a superfície do mar. O efeito é maior na lua nova, quando o Sol e a Lua estão alinhados.
A possibilidade de construção de estações espaciais e satélites que permanecem relativamente próximos ao nosso planeta se deve à energia gravitacional produzida pela Terra. Caso contrário, estações espaciais e satélites artificiais estariam vagando pelo espaço.
Potencial gravitacional da Terra
Suponha que a Terra tenha massa M e um objeto que está acima da superfície da terra à distância r em relação ao centro dela tem massa m.
Neste caso, o potencial gravitacional é determinado a partir da energia gravitacional simplesmente dividindo pela massa do objeto resultante:

Energia potencial perto da superfície da terra
Suponha que a Terra tenha um raio RT e massa M.
Mesmo que a Terra não seja um objeto pontual, o campo em sua superfície é equivalente ao que seria obtido se toda a sua massa M foi concentrado no centro, de modo que a energia gravitacional de um objeto na altura h acima da superfície da Terra é
U (RT + h) = -G.M m (RT + h) ^ - 1
Mas porque h é muito menor que RT, a expressão acima pode ser aproximada por
U = Uo + mgh
Onde g é a aceleração da gravidade, cujo valor médio para a Terra é 9,81 m / s ^ 2.
Então, a energia potencial Ep de um objeto de massa m na altura h acima da superfície da terra é:
Ep (h) = U + Uo = mgh
Na superfície da Terra h = 0, então um objeto na superfície tem Ep = 0. Cálculos detalhados podem ser vistos na figura 3.

Treinamento
Exercício 1: Colapso Gravitacional da Terra
Suponha que nosso planeta sofra um colapso gravitacional devido à perda de energia térmica em seu interior e seu raio caia para a metade de seu valor atual, mas a massa do planeta permanece constante..
Determine qual seria a aceleração da gravidade perto da superfície da Nova Terra e quanto um sobrevivente pesando 50 kg-f pesaria antes do colapso. Aumente ou diminua a energia gravitacional da pessoa e por qual fator.
Solução
A aceleração da gravidade na superfície de um planeta depende de sua massa e de seu raio. A constante de gravitação é universal e funciona igualmente para planetas e exoplanetas.
No caso presente, se o raio da Terra for reduzido pela metade, a aceleração da gravidade da Nova Terra seria 4 vezes maior. Os detalhes podem ser vistos no quadro a seguir.

Isso significa que um super-homem e sobrevivente que pesava 50 kg-f no antigo planeta pesará 200 kg-f no novo planeta..
Por outro lado, a energia gravitacional terá sido reduzida à metade na superfície do novo planeta..
Exercício 2: colapso gravitacional e velocidade de escape
Em referência à situação apresentada no exercício 1, o que aconteceria com a velocidade de escape: aumenta, diminui, por qual fator?
Solução 2
A velocidade de escape é a velocidade mínima necessária para escapar da atração gravitacional de um planeta.
Para calculá-lo, assume-se que um projétil disparado com essa velocidade atinge o infinito com velocidade zero. Além disso, no infinito, a energia gravitacional é zero. Portanto, um projétil que é disparado com velocidade de escape terá energia total zero.
Em outras palavras, na superfície do planeta no momento do tiro, a soma da energia cinética do projétil + a energia gravitacional deve ser zero:
½ m Ve ^ 2 - (G M.m) / RT = 0
Observe que a velocidade de escape não depende da massa do projétil e seu valor ao quadrado é
Ve ^ 2 = (2G M) / RT
Se o planeta entrar em colapso para a metade do raio do original, o quadrado da nova velocidade de escape torna-se o dobro.
Portanto, a nova velocidade de escape cresce e se torna 1,41 vezes a velocidade de escape antiga:
Go '= 1,41 Go
Exercício 3: Energia gravitacional da maçã
Um menino na varanda de um prédio a 30 metros do solo deixa cair uma maçã de 250 g, que após alguns segundos atinge o solo.

a) Qual é a diferença de energia gravitacional da maçã no topo em relação à maçã ao nível do solo?
b) Quão rápido estava a maçã antes de derramar no chão?
c) O que acontece com a energia uma vez que a maçã é achatada contra o solo?
Solução
a) A diferença de energia gravitacional é
m.g.h = 0,250 kg * 9,81 m / s ^ 2 * 30 m = 73,6 J
b) A energia potencial que a maçã possuía aos 30 m de altura é transformada em energia cinética no momento em que a maçã atinge o solo.
½ m v ^ 2 = m.g.h
v ^ 2 = 2.g.h
Substituindo valores e resolvendo, segue-se que a maçã atinge o solo com uma velocidade de 24,3 m / s = 87,3 km / h.
c) Obviamente a maçã se espalha e toda a energia gravitacional acumulada no início é perdida na forma de calor, já que os pedaços de maçã e a zona de impacto são aquecidos, além disso parte da energia também é dissipada na forma de som ondas "splash".
Referências
- Alonso, M. (1970). Física Vol. 1, Fundo Educacional Interamericano.
- Hewitt, Paul. 2012. Ciência Física Conceitual. 5 ª. Ed. Pearson.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, F. (2009). University Physics Vol. 1
- Wikipedia. Energia gravitacional. Recuperado de: es.wikipedia.com
- Wikipedia. Energia gravitacional. Recuperado de: en.wikipedia.com



Ainda sem comentários