
Unidades de energia livre de Helmholtz, como calculá-lo, exercícios resolvidos
O Energia livre de Helmholtz é um potencial termodinâmico que mede o trabalho útil de um sistema fechado em condições de temperatura e volume constantes. A energia livre de Helmholtz é denotada como F y é definido como a diferença da energia interna OU menos produto da temperatura T por entropia S:
F = U - T⋅S
Por ser energia, é medida em Joules no Sistema Internacional (SI), embora outras unidades apropriadas também possam ser ergs (CGS), calorias ou elétron-volts (eV).

A variação negativa da energia de Helmholtz durante um processo é equiparada ao trabalho máximo que o sistema pode realizar em um processo isocórico, ou seja, em volume constante. Quando o volume não é mantido constante, parte desse trabalho pode ser feito no ambiente.
Neste caso, nos referimos a trabalho em que o volume não varia, como o trabalho elétrico: dW = Φdq, com Φ como o potencial elétrico eq como a carga elétrica.
Se a temperatura também for constante, a energia de Helmholtz é minimizada quando o equilíbrio é alcançado. Por tudo isso, a energia Helmholtz é particularmente útil em processos de volume constante. Neste caso, você tem:
- Para um processo espontâneo: ΔF < 0
- Quando o sistema está em equilíbrio: ΔF = 0
- Em um processo não espontâneo: ΔF> 0.
Índice do artigo
- 1 Como a energia livre de Helmholtz é calculada??
- 1.1 Processos espontâneos
- 2 exercícios resolvidos
- 2.1 Exercício 1
- 2.2 Exercício 2
- 3 referências
Como a energia livre de Helmholtz é calculada??
Como afirmado no início, a energia de Helmholtz é definida como "a energia interna U do sistema, menos o produto da temperatura absoluta T do sistema, pela entropia S do sistema":
F = U - T⋅S
É uma função da temperatura T e do volume V. As etapas para visualizar isso são as seguintes:
- A partir da primeira lei da termodinâmica, a energia interna U está relacionada com a entropia S do sistema e seu volume V para processos reversíveis através da seguinte relação diferencial:
dU = dQ - dW = TdS - PdV
Disto se segue que a energia interna U é uma função das variáveis S Y V, portanto:
U = U (S, V)
- Agora tomamos a definição de F e é derivado:
dF = dU - d (TS) = dU - TdS - SdT
- Substituindo ali a expressão diferencial obtida para dU na primeira etapa, permanece:
dF = TdS - PoV - TdS - SdT = -SdT - PoV
- Por fim, conclui-se que F é função da temperatura T e do volume V e pode ser expresso como:
F = F (T, V)
Processos espontâneos
A energia de Helmholtz pode ser aplicada como um critério geral de espontaneidade em sistemas isolados, mas primeiro é conveniente especificar alguns conceitos:
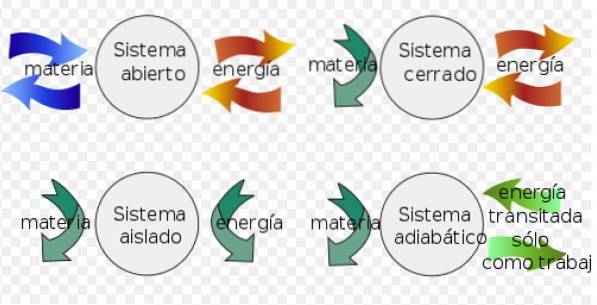
- UMA sistema fechado pode trocar energia com o meio ambiente, mas não pode trocar matéria.
- Em vez de um sistema isolado não troca matéria ou energia com o meio ambiente.
- Finalmente um sistema aberto trocar matéria e energia com o meio ambiente.
Em processos reversíveis, a variação da energia interna é calculada da seguinte forma:
dU = TdS - PoV
Agora suponha um processo em volume constante (isocórico), no qual o segundo termo da expressão anterior tem contribuição zero. Também deve ser lembrado que de acordo com o Desigualdade de Clausius:
dS ≥ dQ / T
Essa desigualdade se aplica a um sistema termodinâmico isolado.
Portanto, para um processo (reversível ou não) em que o volume permanece constante, o seguinte é verdadeiro:
T dS ≥ dU (em volume fixo)
Levando em consideração que:
dF = dU - T dS
Teremos que em um processo isocórico a temperatura constante esteja satisfeito que: dF ≤ 0, como indicado no início.
Assim, a energia F de Helmholtz é uma quantidade decrescente em um processo espontâneo, desde que seja um sistema isolado. F atinge seu valor mínimo e estável quando o equilíbrio reversível é alcançado.
Exercícios resolvidos
Exercício 1
Calcule a variação da energia livre de Helmholtz F para 2 moles de gás ideal a uma temperatura de 300 K durante uma expansão isotérmica que leva o sistema de um volume inicial de 20 litros para um volume final de 40 litros.
Solução
A partir da definição de F:
F = U - T S
Então, uma variação finita de F, chamada ΔF, será:
ΔF = ΔU - T ΔS
Uma vez que a declaração afirma que a temperatura é constante: ΔT = 0. Agora, em gases ideais a energia interna depende apenas de sua temperatura absoluta, mas como é um processo isotérmico, então ΔU = 0 Y ΔF = - T ΔS. Para gases ideais, a mudança de entropia de um processo isotérmico é escrita assim:
ΔS = n.R.ln (Vdois/ V1)
Aplicando esta expressão:
ΔS = 2 moles x 8,314 J / (K mol) x ln (40L / 20L) = 11,53 J / K
Finalmente, a mudança na energia de Helmholtz é:
ΔF = - T ΔS = - 300K x 11,53 J / K = -3457,70 J.
Exercício 2
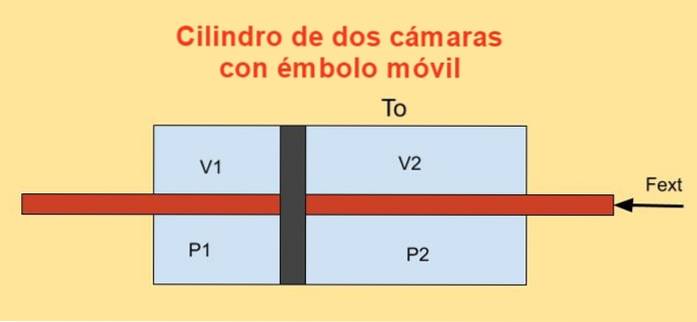
Dentro de um cilindro há um pistão que o divide em duas seções e em cada lado do pistão há n moles de um gás monoatômico ideal, conforme mostrado na figura abaixo.
As paredes do cilindro são bons condutores de calor (diatérmicas) e estão em contato com um reservatório de temperatura Tou.
O volume inicial de cada uma das seções do cilindro é V1i e V2i, enquanto seus volumes finais são V1f e V2f após o deslocamento quase estático. O pistão é movido por meio de um êmbolo que passa hermeticamente pelas duas tampas de cilindro.
É pedido para encontrar:
a) A mudança na energia interna do gás e o trabalho realizado pelo sistema e
b) A variação da energia de Helmholtz.
Solução para
Como o pistão se move quase estaticamente, a força externa aplicada ao pistão deve equilibrar a força devido à diferença de pressão nas duas seções do cilindro..
O trabalho dW realizado por força externa Fext durante uma mudança infinitesimal dx isso é:
dW = - Fext dx = (P1 - Pdois) a dx = P1 dV1 + Pdois dVdois
Onde o relacionamento foi usado dV1 = - dVdois = um dx, sendo para a área do êmbolo. Por outro lado, a variação da energia Helmholtz é:
dF = -SdT - PdV
Uma vez que a temperatura não muda durante o processo, então dT = 0 Y dF = - PoV. Aplicando esta expressão a cada seção do cilindro, temos:
dW = P1 dV1 + Pdois dVdois = - dF1 - dFdois
Sendo F1 Y Fdois as energias Helmholtz em cada uma das câmaras.
O trabalho finito W pode ser calculado a partir da variação finita da energia Helmholtz de cada câmara:
W = -ΔF1 - ΔFdois
Solução b
Para encontrar a mudança na energia de Helmholtz, a definição é usada: F = U - T S. Como em cada câmara existe um gás ideal monoatômico a temperatura constante Tou, a energia interna não muda (ΔU = 0), de modo que: ΔF = - Tou ΔS. O que mais:
ΔS = nR ln (VF/Serrar)
Que ao substituir finalmente permite que o trabalho feito seja:
W = -Tou nR ln (V1f / V1i) -Para nR ln (V2f / V2i) = -ΔF1 -ΔFdois
W = - Para nR ln [(V1f ⋅ V1i) / (V2f .V2i)] = - ΔFtotal
Sendo ΔFtotal a mudança total na energia de Helmholtz.
Referências
- Castanhas E. Exercícios de energia livre. Recuperado de: lidiaconlaquimica.wordpress.com
- Libretexts. Helmholtz Energy. Recuperado de: chem.libretexts.org
- Libretexts. O que são energias livres. Recuperado de: chem.libretexts.org
- Wikipedia. Energia de Helmholtz. Recuperado de: es.wikipedia.com
- Wikipedia. Energia livre de Helmholtz. Recuperado de: en.wikipedia.com


Ainda sem comentários