
Condições de equilíbrio translacional, exemplos, exercícios
Alega-se que um objeto está em equilíbrio translacional quando a soma das forças agindo sobre ele é zero. Isso não significa que haja necessariamente repouso, mas o movimento, caso exista, seria retilíneo uniforme ou exclusivamente rotacional, no caso de um objeto grande..
As condições de equilíbrio mecânico são baseadas nas Leis da Mecânica de Newton. De fato, a primeira lei nos diz que um objeto está em repouso ou se movendo com movimento retilíneo uniforme MRU, desde que nenhuma força resultante atue sobre ele.

Agora, a força resultante ou força resultante é simplesmente a soma vetorial de todas as forças que atuam no objeto. De acordo com a segunda lei de Newton, esta soma deve ser igual ao produto entre a massa e a aceleração, mas se o objeto não for acelerado, esta soma desaparece.
E na ausência de aceleração, surgem as duas possibilidades citadas: o corpo está em repouso, ou seja, não se move, ou se sim, deve estar com MRU. No primeiro caso, falamos de equilíbrio transnacional estático, e no segundo, dinâmico.
O equilíbrio translacional é um fator importante em muitos aspectos da engenharia, por exemplo, na construção. Os elementos que compõem um edifício: vigas, cabos, caixilhos e outros, devem estar em equilíbrio para garantir a estabilidade do recinto.
O equilíbrio translacional também é buscado em estruturas móveis, como escadas rolantes, esteiras transportadoras e na prática de diversos esportes..
Índice do artigo
- 1 Condição de equilíbrio translacional
- 1.1 Diagramas de corpo livre
- 2 Exemplos de equilíbrio translacional
- 2.1 Edifícios e estradas
- 2.2 Livros e objetos nas prateleiras
- 2.3 O mobiliário
- 2.4 Semáforos
- 2.5 Iluminação pública
- 3 Exercício resolvido
- 3.1 Solução
- 4 referências
Condição de equilíbrio translacional
Suponha que várias forças atuem sobre um corpo, que denotamos como F1, Fdois, F3... . Fn, usando negrito para destacar o fato de que as forças são vetores e devem ser adicionadas como tal.
A soma vetorial de todas essas forças é chamada força resultante ou força resultante. Se esse somatório resultar no vetor nulo, a condição para o equilíbrio translacional é atendida:
F1+ Fdois+ F3... .+ Fn = 0
Esta condição pode ser escrita compactamente usando a notação de soma:
∑ Feu = 0
Em termos dos componentes da força resultante, a equação acima, que é vetorial, pode ser dividida em três equações escalares, uma para cada componente da força resultante:
∑ Fix = 0; ∑ FY = 0 e ∑ Fz = 0
Na prática, não é fácil cancelar a soma das forças, porque o atrito é uma força de contato entre as superfícies que dificilmente é totalmente cancelada por qualquer outra força..
Esta é a razão de que objetos reais quase nunca estão isentos de forças externas e, como consequência, é difícil obter equilíbrio translacional.
Portanto, os engenheiros usam mecanismos para reduzir o atrito, como rolamentos e o uso de óleos lubrificantes..
Diagramas de corpo livre
O diagrama de corpo livre é um diagrama no qual as forças que atuam no corpo são desenhadas. Ao buscar o equilíbrio translacional, essas forças devem ser equilibradas. Por exemplo, se uma força vertical direcionada para baixo está agindo, como o peso, então deve haver uma força vertical para cima que tem exatamente a mesma magnitude.
Essa força pode ser fornecida pela mão que sustenta o objeto para que ele não caia, por uma corda ou simplesmente pela superfície de uma mesa.
Se houver uma força tangencial à superfície, como atrito cinético ou estático, deve haver outra força oposta para que o equilíbrio exista. Por exemplo, vamos olhar para o peso pendurado nas cordas mostradas na figura a seguir.
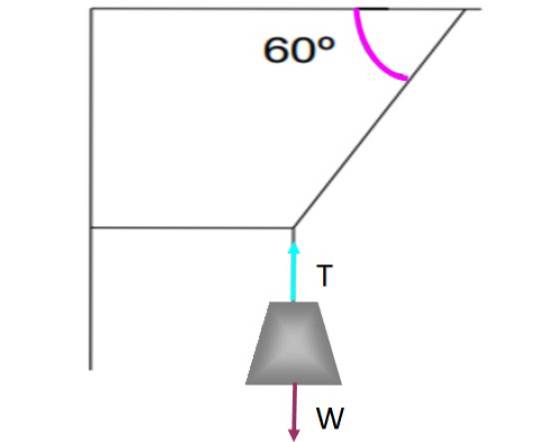
O peso é mantido em equilíbrio translacional e sem movimento, graças à corda vertical que o segura exercendo uma tensão T que compensa o peso C. Cada força foi representada no peso por uma flecha, cada uma de mesmo tamanho e com a mesma direção, mas em direção oposta..
A força de equilíbrio
Suponha que um conjunto de forças atue sobre um objeto. Isso é chamado de sistema de força a partir do qual a resultante pode ser encontrada conforme explicado acima: por adição vetorial de cada uma das forças do sistema.
Bem, a força oposta a esta resultante é chamada força de equilíbrio. Se a força resultante for FR e a força de equilíbrio é E, então:
E + FR = 0
Portanto:
E = - FR
Exemplos de equilíbrio translacional
Muitos objetos que encontramos diariamente, dentro e fora de casa, estão em equilíbrio translacional:
Edifícios e estradas
Prédios e estradas são construídos para permanecer estáveis e não tombar ou desabar. No entanto, em arranha-céus e em edifícios geralmente muito altos, alguma flexibilidade é necessária para resistir à ação do vento..
Livros e objetos nas prateleiras
Livros em uma biblioteca e produtos nas prateleiras das lojas são objetos que permanecem em equilíbrio translacional e não se movem..
A mobília
Os móveis, a TV de tela plana e os quadros nas paredes, assim como as luminárias penduradas no teto, para citar alguns objetos, estão em equilíbrio translacional..
Luzes de trânsito
Os semáforos são presos por postes e cabos, para que não caiam. No entanto, sabemos que o vento os faz balançar.
Iluminação pública
Os postes de luz também estão em equilíbrio translacional, fixados nos postes, como o poste da imagem principal..
Exercício resolvido
Quão grande deve ser a força Fs de atrito estático de forma que a caixa da figura permaneça em repouso no meio do plano inclinado em um ângulo α de 37º? A massa da caixa é m = 8 kg.
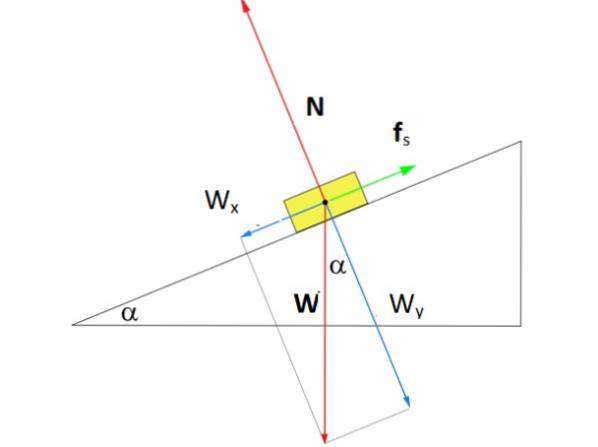
Solução
A figura mostra o diagrama de corpo livre da caixa no avião. Existem três forças agindo sobre ele: peso C, dirigido verticalmente para baixo, o normal N, que é a força perpendicular exercida pela superfície do plano na caixa e, finalmente, a força de atrito estático Fs que se opõe à caixa deslizando morro abaixo.
A condição de equilíbrio translacional afirma que:
C + N + Fs = 0
Mas devemos lembrar que esta é uma soma vetorial e para realizá-la é necessário decompor as forças em componentes ao longo dos eixos coordenados.
Na figura, um sistema de coordenadas foi desenhado no qual o eixo x corre paralelo à superfície do plano inclinado. Com esta escolha, o atrito estático recai sobre o referido eixo, enquanto o normal fica no eixo y. O peso é a única força inclinada e deve ser quebrada com a ajuda da trigonometria:
Cx = W. sen α
CY = W. cos α
A soma das forças ao longo de cada eixo é:
∑ FY = N - WY = 0
∑ Fx = fs - Cx = 0
Desta última equação segue-se que:
Fs = Wx
E como Wx = W. sen α e a magnitude do peso por sua vez é W = m.g, onde g é o valor da gravidade, então a magnitude do atrito estático é simplesmente:
Fs = m⋅g⋅sen α = 8 kg × 9,8 m / sdois × sen 37º = 47,2 N.
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill.
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 2. Dynamics. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Física. 2ª Ed. McGraw Hill.
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 1. 7mãe. Ed. Cengage Learning.
- Tippens, P. 2011. Physics: Concepts and Applications. 7ª Edição. Colina Mcgraw.


Ainda sem comentários