
Tensão de cisalhamento como é calculada e os exercícios resolvidos
É conhecido como esforço cortante O resultado da aplicação de duas forças paralelas a uma superfície e na direção oposta. Desta forma, um objeto pode ser dividido em duas partes, fazendo com que as seções deslizem uma sobre a outra..
As forças de cisalhamento diretas são aplicadas diariamente em tecidos, papéis ou metais, exercidas por tesouras, guilhotinas ou tesouras. Eles também aparecem em estruturas como parafusos ou cavilhas, cavilhas, vigas, cunhas e soldas..

É necessário esclarecer que nem sempre se pretende seccionar ou cortar, mas a tensão de cisalhamento tende a deformar o objeto sobre o qual é aplicada; portanto, vigas sujeitas a tensões de cisalhamento tendem a ceder com seu próprio peso. Os exemplos a seguir esclarecem o ponto.
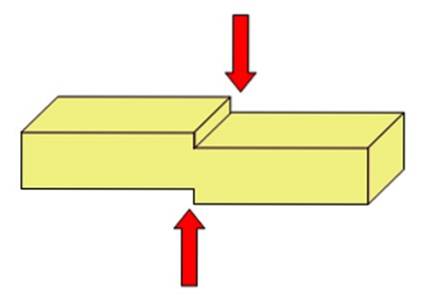
A Figura 2 mostra um diagrama simples para ilustrar o acima. É um objeto sobre o qual duas forças atuam em direções opostas. Existe um plano de corte imaginário (não é desenhado) e as forças atuam uma em cada lado do plano, cortando a barra em duas.
No caso da tesoura: cada lâmina ou gume aplica uma força na seção transversal (circular) do objeto a ser cortado, separando-o também em duas partes, como o fio da figura 1.
Índice do artigo
- 1 A tensão de cisalhamento pode causar deformação
- 2 Como é calculada a tensão de cisalhamento??
- 3 Tensão de cisalhamento e deformação
- 4 exercícios resolvidos
- 4.1 - Exercício 1
- 4.2 - Exercício 2
- 5 referências
A tensão de cisalhamento pode causar deformação
Você pode tentar exercer uma força de corte deslizando a mão sobre a capa de um livro fechado. A outra tampa deve permanecer fixa na mesa, o que pode ser conseguido apoiando a mão livre para que não se mova. O livro vai se deformar um pouco com essa ação, conforme descrito na figura a seguir:
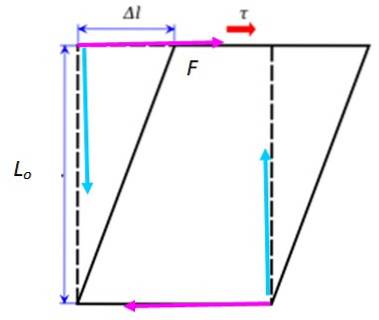
Se esta situação for analisada com cuidado, as duas forças já mencionadas, mas desta vez aplicadas horizontalmenteem fúcsia). Uma é a de sua mão de um lado e a outra é aplicada pela superfície da mesa no lado oposto do livro que é fixado.
O livro não gira, embora essas forças possam causar um torque ou momento líquido. Para evitar isso, existem as outras duas forças verticais (em turquesa); o aplicado com a outra mão e o normal exercido pela mesa, cujo momento líquido atua no sentido oposto, impedindo o movimento de rotação.
Como é calculada a tensão de cisalhamento?
As tensões de cisalhamento aparecem até mesmo dentro do corpo humano, uma vez que o sangue circulante exerce continuamente forças tangenciais no interior dos vasos sanguíneos, causando pequenas deformações nas paredes..
Sua consideração é importante para determinar as chances de uma estrutura falhar. Nas forças de cisalhamento, não só a força é levada em consideração, mas também a área sobre a qual ela atua.
Isso é compreendido imediatamente pegando duas barras cilíndricas do mesmo comprimento, feitas do mesmo material, mas de espessura diferente, e submetendo-as a tensões crescentes até que se rompam..
Obviamente, as forças necessárias serão bem diferentes, porque uma barra é mais fina que a outra; entretanto o esforço será o mesmo.
A tensão de cisalhamento é indicada pela letra grega τ (tau) e é calculado como o quociente entre a magnitude da força aplicada F e a área PARA da superfície sobre a qual atua:
τmédia= F / A
O esforço assim calculado é aquele que produz uma força média na superfície em questão, uma vez que a força não atua sobre um único ponto da superfície, mas se distribui por toda ela e não uniformemente. No entanto, a distribuição pode ser representada por uma força resultante atuando em um ponto particular.
As dimensões da tensão de cisalhamento são forças na superfície. Em unidades do sistema internacional, eles correspondem a newton / metro quadrado, uma unidade chamada Pascal e abreviada como Pa.
São as mesmas unidades de pressão, portanto as unidades do sistema inglês como libra-força / pé dois e libra-força / polegadadois também são apropriados.
Tensão de cisalhamento e deformação
Em muitas situações, a magnitude da tensão de cisalhamento é proporcional à deformação causada no objeto, como no livro de exemplo anterior, que retornará às suas dimensões originais assim que a mão for removida. Em tal caso:
Esforço cortante ∝ Deformação da unidade
A constante de proporcionalidade, neste caso, é o módulo de cisalhamento, módulo de rigidez ou módulo de cisalhamento (G):
Tensão de cisalhamento = Módulo de cisalhamento x Deformação unitária
τ = G. γ
Com γ = ΔL / Lou, onde Δeu é a diferença entre o comprimento final e inicial. Ao combinar as equações fornecidas, uma expressão para a deformação causada pelo estresse pode ser encontrada:
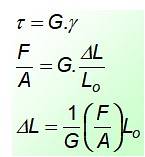
O valor da constante G É encontrada em tabelas e suas unidades são as mesmas das tensões, já que a deformação é adimensional. Quase sempre o valor de G é metade ou um terço do valor de E, módulos de elasticidade.
Na verdade, eles estão relacionados pela expressão:
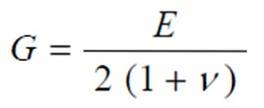
Onde ν é o módulo de Poisson, outra constante elástica do material cujo valor está entre 0 e ½. Precisamente por esta razão G, por sua vez, está entre E / 3 e E / 2.
Exercícios resolvidos
-Exercício 1
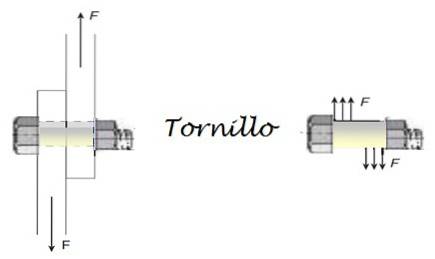
Para unir duas placas de ferro é utilizado um parafuso de aço, que deve resistir a forças de cisalhamento de até 3.200 N. Qual é o diâmetro mínimo do parafuso se o fator de segurança é 6,0? O material é conhecido por conter até 170 x 106 N / mdois.
Solução
A tensão de cisalhamento a que o parafuso é submetido provém das forças mostradas na figura abaixo. O fator de segurança é uma quantidade adimensional e está relacionado ao estresse máximo permitido:
Tensão de cisalhamento = F / A = Tensão máxima permitida / fator de segurança
Portanto, a área é:
A = F x fator de segurança / tensão de cisalhamento = 3200 x 6/170 x 106 = 0,000113 mdois
A área do parafuso é dada por πDdois/ 4, portanto, o diâmetro é:
Ddois= 4 x A / π = 0,000144 mdois
D = 0,012 m = 12 mm.
-Exercício 2
Um tarugo de madeira ou tarugo é usado para evitar que a polia gire sob tensão T1 Y Tdois, em relação a um eixo de 3 polegadas. As dimensões do pino são mostradas na figura. Encontre a magnitude da tensão de cisalhamento no bloco, se as forças mostradas atuam na polia:
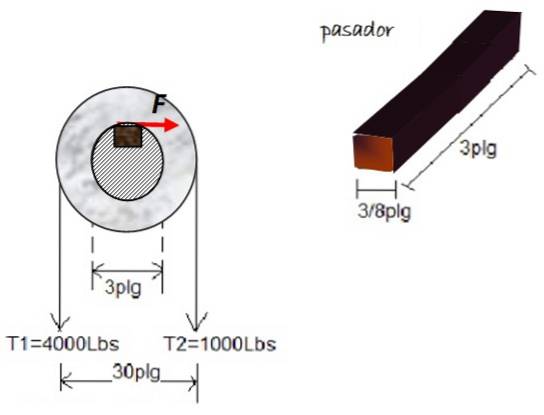
Solução
T1 produz um torque no sentido anti-horário na polia, ao qual um sinal positivo é atribuído, enquanto Tdois produz torque no sentido horário com sinal negativo. O braço de alavanca mede 15 polegadas para cada tensão. Portanto:
Torque líquido = força de 4000 libras. 15 polegadas - força de 1000 libras. 15 polegadas = 45.000 libras-força. polegada
O bloco de madeira não deve girar, portanto os momentos em relação ao centro do bloco devem ser zero. F representa a força média na superfície:
45.000 - F.d = 0
Com d = 1,5 polegadas, portanto:
F x 1,5 = 45.000
F = 30.000 libras-força
Esta força causa uma tensão de cisalhamento de magnitude:
τ = F / A = 30.000 libras-força / (3/8 x 3) polegadasdois = 2,67 x 104 libra-força / polegadadois
Referências
- Beer, F. 2010. Mecânica dos materiais. 5 ª. Edição. McGraw Hill. 7 - 9.
- Fitzgerald, 1996. Mecânica dos Materiais. Alfa Ômega. 21-23.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Mecânica dos materiais. 6º. Edição. Pearson Education. 22-25
- Valera Negrete, J. 2005. Notes on General Physics. UNAM. 87-98.
- Wikipedia. Tensão de cisalhamento. Recuperado de: en.wikipedia.org.



Ainda sem comentários