
Fórmula de tensão de tração e equações, cálculo, exercícios
O Tensão de estresse É definida como a força perpendicular à área por unidade de área aplicada a um objeto em suas extremidades para exercer tração sobre ele, graças à qual ele se alonga. Suas dimensões são força / área e na forma matemática podemos expressá-lo assim:
τ = F / A
A unidade de esforço do Sistema Internacional de Unidades é a mesma utilizada para a pressão: o pascal, abreviado Pa, que equivale a 1 newton / mdois.

No esforço de tração, existem duas forças que são aplicadas na mesma direção e em direções opostas, que alongam o corpo. Se originalmente o comprimento do objeto era Lou, ao aplicar a tensão de tração, o novo comprimento é L e o alongamento ΔL é calculado por:
ΔL = L - Lou
Objetos sólidos têm elasticidade em maior ou menor grau, o que significa que quando a tensão de tração desaparece, eles voltam às suas dimensões originais..
Isso acontece desde que a tensão não seja tão grande a ponto de causar deformação permanente. Borracha, borracha ou materiais de borracha são bons para fazer objetos elásticos e cabelos e pele, entre outros, também têm essa qualidade..
Índice do artigo
- 1 estirpe
- 2 Como é calculada a tensão de tração? (Exemplos)
- 2.1 Exemplo de cálculo
- 3 exercícios resolvidos
- 4 - Exercício 1
- 5 - Exercício 2
- 6 referências
Deformação da unidade
Ao estudar como os corpos são deformados sob estresse, é muito conveniente definir o conceito de cepa, uma quantidade adimensional. A deformação é denotada pela letra grega δ ("delta" minúscula) e é calculada da seguinte forma:
δ = ΔL / Lou
A tensão é usada para avaliar comparativamente a deformação do objeto sob tensão. Vamos ver desta forma: esticar 1 cm de uma barra de 1 metro de comprimento não é o mesmo que esticar 1 cm de uma barra de 10 m de comprimento. No primeiro caso, a deformação é muito mais significativa do que no segundo.
Como é calculada a tensão de tração? (Exemplos)
O físico inglês contemporâneo de Newton, chamado Robert Hooke (1635-1703), investigou as propriedades elásticas dos corpos e estabeleceu a lei que leva seu nome. Com ele, a tensão aplicada está relacionada à deformação experimentada quando a tensão é pequena:
Tensão ∝ Tensão (unidade)
É lógico esperar que quanto maior a tensão de tração, maior será o alongamento. Fazendo uso das definições fornecidas acima:
τ ∝ δ
A constante de proporcionalidade necessária para estabelecer a igualdade é denotada por Y e é conhecida como módulo de Young ou módulo de elasticidade, característica dos materiais:
τ = Y⋅δ
O módulo de Young tem as mesmas unidades de tensão de tração, uma vez que a deformação é adimensional.
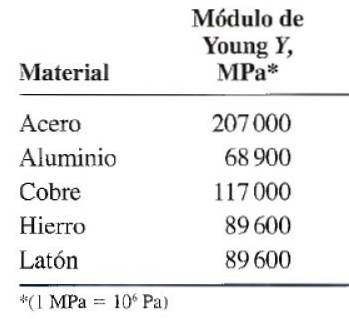
Portanto, uma forma de calcular a tensão de tração em um corpo com propriedades elásticas é medindo a deformação e conhecendo seu módulo de Young. Esta quantidade foi determinada experimentalmente para muitos materiais e é tabulada.
Exemplo de cálculo
Suponha que um fio de aço temperado com diâmetro de 3 mm seja submetido a uma tensão de tração, pendurado nele um peso de 250 N, qual seria a magnitude dessa tensão?
Bem, podemos usar a definição de tensão de tração como a razão entre a força perpendicular à superfície e a área dessa superfície. Vamos primeiro calcular a área, assumindo um fio de seção transversal circular:
A = π. (d / 2)dois = π. (ddois / 4)
O diâmetro do fio é de 3 mm e essas unidades devem ser transformadas em metros:
d = 3 x 10-3 m.
A = π. (3 x 10-3 m)dois / 4 = 7,07 x 10-6 mdois.
A tensão de tração é produzida pelo peso pendurado no fio, que é aplicado perpendicularmente à sua seção transversal, portanto:
τ = 250 N / 7,07 x 10-6 mdois = 3,5 x 10 7 Pa
O pascal é uma unidade bastante pequena, portanto, múltiplos não são incomuns. Saber que 1 mega-pascal (MPa) é 106 pascal, a tensão de tração permanece:
τ = 35 MPa
Exercícios resolvidos
- Exercício 1
O módulo de elasticidade de uma haste é 4 x 10onze Pa. Que deformação é obtida pela aplicação de uma tensão de tração de 420 MPa?
Solução
A equação a ser usada é:
τ = Y⋅δ
Com ele calculamos a deformação:
δ = τ / Y = 420 x 106 Pa / 4 x 10onze Pa = 0,00105
δ = ΔL / Lou
Portanto, a cepa ΔL é:
ΔL = 0,00105 Lou
Se, por exemplo, a haste tinha originalmente 1 metro de comprimento, com essa tensão de tração ela se estende apenas 0,00105 m = 1,05 mm.
- Exercício 2
Um fio de aço tem 1,50 m de comprimento e 0,400 mm de diâmetro. Uma extremidade é conectada ao teto e um refletor de aterramento é conectado à outra. m = 1,50 kg, que é liberado. Calcular:
a) O alongamento do fio.
b) Deformação e porcentagem de deformação. É possível que o fio se quebre sob o peso do refletor??
Solução
O fio vai se esticar, pois ao pendurar o refletor ele é submetido a uma tensão de tração. A força que produz este esforço é o peso do refletor.
O peso de um objeto de massa m é o produto da massa pelo valor da aceleração da gravidade, portanto:
F = 1,50 kg x 9,8 m / sdois = 14,7 N
A área da seção transversal do fio é necessária:
A = π. (ddois / 4) = π x (0,4 x 10-3 m) 2/4 = 1,26 x 10-7 mdois.
Com esses resultados, calcula-se o esforço exercido pelo peso no fio:
τ = 14,7 N / 1,26 x 10-7 mdois = 1,17 x 108 Pa
O fio tem um comportamento elástico, portanto é válido supor que a lei de Hooke seja cumprida:
τ = Y⋅δ
A partir da tabela de módulo de elasticidade, encontramos que para aço Y = 207 x 109 Pa. Além disso, a cepa é:
δ = ΔL / Lou
Substituindo o esforço na equação:
τ = Y⋅δ = Y⋅ (ΔL / Lou)
Portanto, o alongamento é:
ΔL = Lou τ / Y =
= 1,50 m x 1,17 x 108 Pa / 207 x 109 Pa = 8,5 x 10-4 m = 0,849 mm.
A tensão do fio é:
δ = ΔL / Lou = 8,5 x 10-4 m / 1,5 m = 5,652 x 10-4
Se expressarmos como uma porcentagem, a deformação da unidade percentual é 0,0565%, menos de 0,1%, portanto, espera-se que o fio resista bem ao peso do refletor sem quebrar, já que a deformação que experimenta não é muito grande em comparação . ao comprimento original.
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill.
- Beer, F. 2010. Mecânica dos materiais. McGraw Hill. 5 ª. Edição.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall.
- Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1.
- Valera Negrete, J. 2005. Notes on General Physics. UNAM.



Ainda sem comentários