UMA espaço vetorial é um conjunto não vazio V= ou, v, C,…, cujos elementos são vetores. Com eles são realizadas algumas operações importantes, entre as quais se destacam:
- Soma entre dois vetores u + v quais resultados z, que pertence ao conjunto V.
- Multiplicação de um número real α por um vetor v: α v o que dá outro vetor Y que pertence a V.
Para denotar um vetor, usamos negrito (v é um vetor), e para escalares ou números, letras gregas (α é um número).
Índice do artigo
Para que um espaço vetorial seja fornecido, os oito axiomas a seguir devem ser atendidos:
1-Comutável: ou +v = v +ou
2-Transitividade: (ou + v) + C = ou + ( v + C)
3-Existência do vetor nulo 0 tal que 0 + v = v
4-Existência do oposto: o oposto de v isso é (-v) , já que v + (-v) = 0
5-Distributividade do produto em relação à soma do vetor: α ( ou + v ) = αou +αv
6-Distributividade do produto em relação à soma escalar: (α + β)v = αv +βv
7-Associatividade do produto escalar: α (β v) = (α β)v
8-O número 1 é o elemento neutro, pois: 1v = v
Os vetores no plano (R²) são um exemplo de um espaço vetorial. Um vetor no plano é um objeto geométrico que possui magnitude e direção. É representado por um segmento orientado pertencente ao referido plano e com um tamanho proporcional à sua magnitude.
A soma de dois vetores no plano pode ser definida como a operação de translação geométrica do segundo vetor após o primeiro. O resultado da soma é o segmento orientado que começa na origem do primeiro e atinge a ponta do segundo.
Na figura pode-se observar que a soma em R² é comutativa.
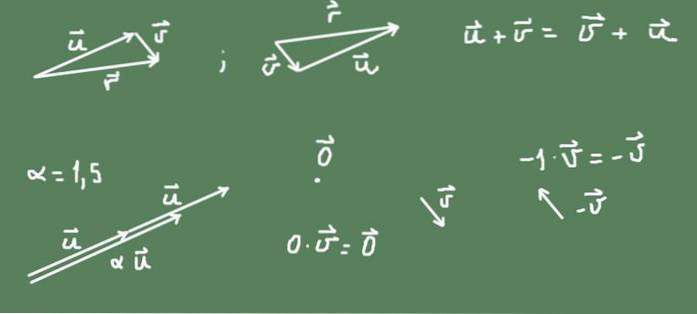
O produto de um número α e de um vetor também é definido. Se o número for positivo, a direção do vetor original é mantida e o tamanho é α vezes o vetor original. Se o número for negativo, a direção é oposta, e o tamanho do vetor resultante é o valor absoluto do número.
O vetor oposto a qualquer vetor v isso é -v = (- 1) v.
O vetor nulo é um ponto no plano R², e o número zero vezes um vetor resulta no vetor nulo.
Tudo o que foi dito está ilustrado na figura 2.
O conjunto P de todos os polinômios de grau menor ou igual a dois, incluindo grau zero, formam um conjunto que satisfaz todos os axiomas de um espaço vetorial.
Seja o polinômio P (x) = a x² + b x + c e Q (x) = d x² + e x + f
A soma de dois polinômios é definida: P (x) + Q (x) = (a + d) x² + (b + e) x + (c + f)
A soma dos polinômios pertencentes ao conjunto P é comutativo e transitivo.
O polinômio nulo pertencente ao conjunto P é aquele que tem todos os seus coeficientes iguais a zero:
0 (x) = 0 x² + 0 x + 0
A soma de um escalar α por um polinômio é definida como: α P (x) = α ∙ a x² + α ∙ b x + α ∙ c
O polinômio oposto de P (x) é -P (x) = (-1) P (x).
De todo o exposto, segue-se que o conjunto P de todos os polinômios de grau menor ou igual a dois, é um espaço vetorial.
O conjunto M de todas as matrizes de m linhas x n colunas cujos elementos são números reais formam um espaço vetorial real, no que diz respeito às operações de adição de matrizes e produto de um número por uma matriz.
O conjunto F de funções contínuas de variável real, forma um espaço vetorial, uma vez que é possível definir a soma de duas funções, a multiplicação de um escalar por uma função, a função nula e a função simétrica. Eles também cumprem os axiomas que caracterizam um espaço vetorial.
A base de um espaço vetorial é definida como um conjunto de vetores linearmente independentes, de modo que a partir de uma combinação linear deles qualquer vetor desse espaço vetorial pode ser gerado.
A combinação linear de dois ou mais vetores consiste em multiplicar os vetores por algum escalar e, em seguida, adicioná-los vetorialmente.
Por exemplo, no espaço vetorial de vetores em três dimensões formado por R³, a base canônica definida pelos vetores unitários (de magnitude 1) é usada eu, j, k.
Onde eu = (1, 0, 0); j = (0, 1, 0); k = (0, 0, 1). Estes são os vetores cartesianos ou canônicos.
Qualquer vetor V pertencente a R³ é escrito como V = a eu + b j + c k, que é uma combinação linear dos vetores de base eu, j, k. Os escalares ou números a, b, c são conhecidos como os componentes cartesianos de V.
Também é dito que os vetores de base de um espaço vetorial formam um conjunto gerador do espaço vetorial.
A dimensão de um espaço vetorial é o número cardinal de uma base vetorial para esse espaço; ou seja, o número de vetores que compõem a referida base.
Este cardinal é o número máximo de vetores linearmente independentes desse espaço vetorial e, ao mesmo tempo, o número mínimo de vetores que formam um conjunto gerador desse espaço.
As bases de um espaço vetorial não são únicas, mas todas as bases do mesmo espaço vetorial têm a mesma dimensão.
Um subespaço vetorial S de um espaço vetorial V é um subconjunto de V no qual as mesmas operações são definidas como em V e cumpre todos os axiomas do espaço vetorial. Portanto, o subespaço S também será um espaço vetorial.
Um exemplo de subespaço vetorial são os vetores que pertencem ao plano XY. Este subespaço é um subconjunto de um espaço vetorial de dimensionalidade maior que o conjunto de vetores pertencentes ao espaço tridimensional XYZ.
Outro exemplo de um subespaço vetorial S1 do espaço vetorial S formado por todas as matrizes 2 × 2 com elementos reais é definido abaixo:
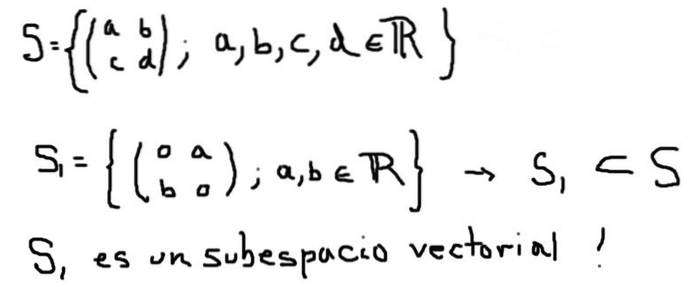
Por outro lado, S2 definido abaixo, embora seja um subconjunto de S, não forma um subespaço vetorial:
Deixe os vetores serem V1= (1, 1, 0); V2= (0, 2, 1) e V3= (0, 0, 3) em R³.
a) Mostre que eles são linearmente independentes.
b) Mostre que eles formam uma base em R³, uma vez que qualquer triplo (x, y, z) pode ser escrito como uma combinação linear de V1, V2, V3.
c) Encontre os componentes do triplo V = (-3,5,4) na base V1, V2, V3.
O critério para demonstrar independência linear consiste em estabelecer o seguinte conjunto de equações em α, β e γ
α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)
No caso de a única solução para este sistema ser α = β = γ = 0 então os vetores são linearmente independentes, caso contrário eles não são.
Para obter os valores de α, β e γ, propomos o seguinte sistema de equações:
α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0
α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0
α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0
O primeiro leva a α = 0, o segundo α = -2 ∙ β, mas como α = 0, então β = 0. A terceira equação implica que γ = (- 1/3) β, mas como β = 0 então γ = 0.
Conclui-se que é um conjunto de vetores linearmente independentes em R³ .
Agora vamos escrever o triplo (x, y, z) como uma combinação linear de V1, V2, V3.
(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)
α ∙ 1 + β ∙ 0 + γ ∙ 0 = x
α ∙ 1 + β ∙ 2 + γ ∙ 0 = y
α ∙ 0 + β ∙ 1 + γ ∙ 3 = z
Onde você tem:
α = x
α + 2 β = y
β + 3 γ = z
O primeiro indica α = x, o segundo β = (y-x) / 2 e o terceiro γ = (z- y / 2 + x / 2) / 3. Desta forma, encontramos os geradores de α, β e γ de qualquer trinca de R³
Vamos prosseguir para encontrar os componentes do triplo V = (-3,5,4) na base V1, V2, V3.
Substituímos os valores correspondentes nas expressões encontradas acima pelos geradores.
Nesse caso, temos: α = -3; β = (5 - (- 3)) / 2 = 4; γ = (4- 5/2 + (- 3) / 2) / 3 = 0
Quer dizer que:
(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)
Por último:
V = -3 V1 + 4 V2 + 0 V3
Concluimos que V1, V2, V3 formam uma base no espaço vetorial R³ de dimensão 3.
Expresse o polinômio P (t) = t² + 4t -3 como uma combinação linear de P1 (t) = t² -2t + 5, P2 (t) = 2t² -3t e P3 (t) = t + 3.
P (t) = x P1 (t) + y P2 (t) + z P3 (t)
onde os números x, y, z devem ser determinados.
Multiplicar e agrupar termos com o mesmo grau em t dá:
t² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)
O que nos leva ao seguinte sistema de equações:
x + 2y = 1
-2x -3y + z = 4
5x + 3z = -3
As soluções deste sistema de equações são:
x = -3, y = 2, z = 4.
Quer dizer que:
P (t) = -3 P1 (t) + 2 P2 (t) + 4 P3 (t)
Mostre que os vetores v1= (1, 0, -1, 2); v2= (1, 1, 0, 1) e v3= (2, 1, -1, 1) de R⁴ são linearmente independentes.
Nós combinamos linearmente os três vetores v1, v2, v3 e exigimos que a combinação adicione o elemento nulo de R⁴
para v1 + b v2 + c v3 = 0
Quer dizer,
a (1, 0, -1, 2) + b (1, 1, 0, 1) + c (2, 1, -1, 1) = (0, 0, 0, 0)
Isso nos leva ao seguinte sistema de equações:
a + b + 2 c = 0
b + c = 0
-a - c = 0
2 a + b + c = 0
Subtraindo o primeiro e o quarto temos: -a + c = 0 que implica a = c.
Mas se olharmos para a terceira equação, temos que a = -c. A única maneira que a = c = (- c) é válida é que c é 0 e, portanto, a também será 0.
a = c = 0
Se substituirmos este resultado na primeira equação, então concluímos que b = 0.
Finalmente a = b = c = 0, de modo que se pode concluir que os vetores v1, v2 e v3 são linearmente independentes.
Ainda sem comentários