
Conceito de espelho convexo, características, exemplos
O espelho convexo ou divergente é um espelho curvo, quase sempre de forma esférica e com a superfície refletora do lado externo da esfera, como os enfeites da árvore de Natal. Graças aos espelhos convexos é possível obter uma grande variedade de imagens dependendo da localização do objeto e por isso têm tantos usos..
Por exemplo, os espelhos que são colocados nas ruas para facilitar o trânsito de veículos em cruzamentos estreitos são convexos, pois produzem uma imagem com amplo campo visual.
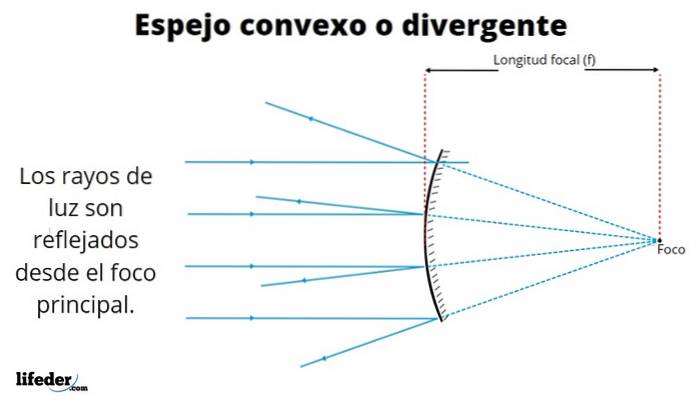
As imagens assim formadas são diversas, dependendo do local onde o objeto é colocado. A imagem acima mostra os raios paralelos de uma fonte distante, como o sol..
Os raios são refletidos de acordo com a lei da reflexão, que indica que o ângulo de incidência do raio é o mesmo com o qual ele é refletido. Como podemos ver, os raios refletidos se separam - eles não se cruzam - quando deixam a superfície especular, razão pela qual este tipo de espelho também é conhecido como divergente.
Quando os reflexos se estendem por trás do espelho - linhas tracejadas na figura - eles se cruzam em um ponto F chamado de foco..
Índice do artigo
- 1 Características dos espelhos convexos
- 2 Formação de imagem no espelho convexo
- 3 exemplos e aplicações
- 3.1 Espelhos para prevenir acidentes de trânsito
- 3.2 Espelhos para vigilância
- 3.3 Espelhos retrovisores
- 3.4 Telescópio Cassegrain
- 4 Equações do espelho convexo
- 4.1 Ampliação do espelho
- 4.2 Relação entre o objeto e sua imagem no espelho convexo
- 5 tópicos de interesse
- 6 referências
Características de espelhos convexos

O espelho convexo possui as seguintes características (ver imagem acima):
-Os pontos notáveis do espelho são:
- C o centro, que coincide com o centro da esfera à qual o espelho pertence.
- F o foco, onde os raios refletidos atrás do espelho convergem.
- Seu vértice P, que corresponde ao centro da superfície esférica e é colinear com C e F.
-Ter eixo óptico ou Eixo principal, que é a linha perpendicular à superfície especular. Os raios que atingem apenas o eixo óptico são refletidos na mesma direção.
-O centro da esfera à qual o espelho pertence está no ponto C e r é seu raio. A C é conhecido como centro de curvatura, enquanto que r é o Raio de curvatura e indica quão curvo é o espelho: quanto menor r, mais acentuada é a forma convexa.
-O ponto de intersecção dos raios refletidos é conhecido como Ponto focal do espelho. A distância entre F e P é aproximadamente r/dois:
f = r / 2
Esta expressão é válida para espelhos cujo tamanho é muito menor que seu raio de curvatura.
-A imagem que se forma é menor e também virtual, pois fica atrás do espelho, como veremos a seguir..
Formação de imagem no espelho convexo
Para saber o que se forma a imagem no espelho convexo, utiliza-se o tratamento de raios, que consiste em representar os raios de luz que saem do objeto por meio de linhas retas..
Esses raios são refletidos na superfície do espelho e os raios refletidos também são desenhados. O método do raio é aplicável a qualquer tipo de espelho, não apenas aos convexos.
Ao prolongar os raios refletidos, eles se cruzam em um determinado ponto, e é precisamente aí que a imagem é formada. As extensões dos raios refletidos que vêm de um objeto estendido, como uma árvore, são mostradas na figura abaixo por linhas tracejadas.
Na figura abaixo, três raios são desenhados do objeto, muito particulares e fáceis de desenhar, assim como seus reflexos:
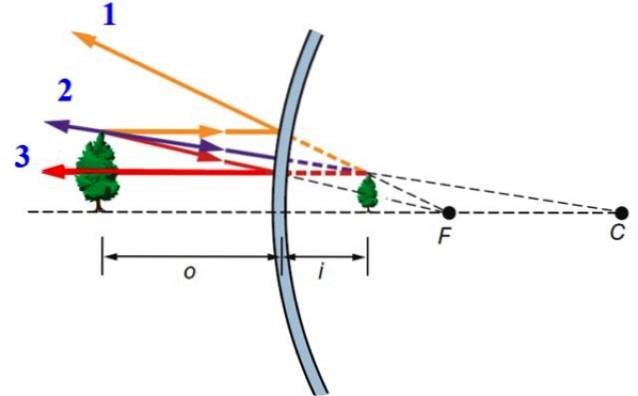
-Raio 1, incidente paralelo ao eixo óptico.
-Raio 2, que cai de tal forma que o prolongamento do raio refletido passa justamente pelo foco do espelho, ou seja, o ponto F. Este raio é refletido em uma direção paralela ao eixo óptico.
-Finalmente o raio 3, que chega perpendicular à superfície esférica, e por este motivo é refletido na mesma direção.
Em princípio, este procedimento é aplicado a cada ponto da árvore, mas com a informação obtida a partir dos 3 raios desenhados, basta encontrar a imagem do objeto: ele é formado atrás do espelho, é reto e menor que o original.
Exemplos e aplicações
Muitas superfícies esféricas altamente polidas atuam como espelhos convexos, por exemplo, enfeites de Natal brilhantes e prateados, bem como colheres de aço novas e brilhantes.
Além disso, os espelhos convexos têm muitas aplicações práticas, por exemplo:
Espelhos para prevenir acidentes de trânsito

Espelhos convexos em ruas e avenidas ajudam a prevenir acidentes, pois permitem que você veja o tráfego vindo das esquinas.
Espelhos para vigilância
Os espelhos convexos são frequentemente usados em lojas e bancos para detectar ladrões, bem como para evitar colisões entre pessoas e empilhadeiras que se movem pelos corredores e entre as prateleiras..
Espelhos retrovisores

Carros e motocicletas têm espelhos retrovisores convexos, que produzem imagens um pouco menores, mas cobrem mais campo de visão do que espelhos planos..
Telescópio Cassegrain

Um dos espelhos do telescópio refletor Cassegrain, o espelho secundário, é convexo, embora não seja esférico e serve para refletir a imagem em direção ao espelho principal do telescópio.
Equações de espelho convexo
Vamos considerar os triângulos retângulos na figura a seguir, determinados pelo raio 1, que vem do topo da flecha, seu reflexo e sua extensão.
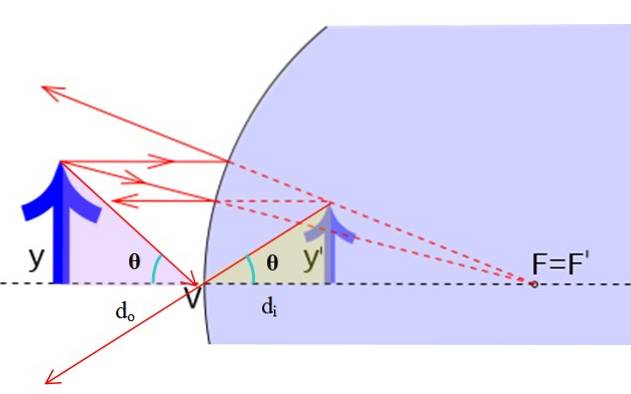
A imagem original tem altura y, enquanto a altura da imagem virtual é y ' . É verdade que:
tan θ = y / dou = y '/ deu
Ampliação do espelho
A proporção entre a altura da imagem e a altura do objeto é o ampliação do espelho, que é chamado assim, mesmo que a imagem obtida seja menor que o objeto real. Denotamos isso por m:
m = y '/ y = deu / dou
Relação entre o objeto e sua imagem no espelho convexo
Agora vamos considerar esta outra figura, onde a região AVF pode ser considerada aproximadamente como um triângulo retângulo, uma vez que a curvatura do espelho não é muito acentuada. Portanto:
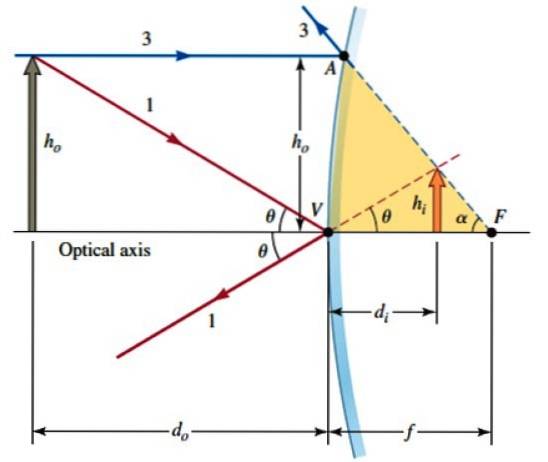
AV ≈ hou
Então:
tan α = h



1- (deu / f) = deu / dou
Ao dividir tudo por deu:


Portanto, como F Y deu estão atrás do espelho, um sinal de menos é colocado antes deles, enquanto para a distância dou isso não é necessário, pois está na frente do espelho. Assim, a equação anterior é:

Assuntos de interesse
Espelho côncavo.
Referências
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 2. Mc Graw Hill.
- Giambattista, A. 2010. Física. 2ª Ed. McGraw Hill.
- Katz, D. 2017. Physics for Scientists and Engineers. Cengage Learning.
- Thomas, W. 2008. Física Conceitual. Colina Mcgraw.
- Tippens, P. 2011. Physics: Concepts and Applications. 7ª Edição. Colina Mcgraw.



Ainda sem comentários