
História da estatística descritiva, características, exemplos, conceitos
O Estatística descritiva é o ramo da Estatística responsável por coletar e organizar informações sobre o comportamento de sistemas com muitos elementos, conhecidos genericamente pelo nome de população.
Para isso, utiliza técnicas numéricas e gráficas, por meio das quais apresenta informações, sem fazer previsões ou inferências sobre a população de onde provém..

Índice do artigo
- 1 história
- 1.1 Idade Antiga
- 1.2 Renascença
- 1.3 Idade Moderna
- 2 Características da estatística descritiva
- 3 O que são estatísticas descritivas para?
- 3.1 Economia
- 3.2 Física e Mecânica
- 3.3 Remédio
- 3.4 Nutrição
- 4 Exemplos de estatísticas descritivas
- 4.1 Exemplo 1
- 4.2 Exemplo 2
- 4.3 Exemplo 3
- 5 conceitos básicos de estatística descritiva
- 5.1 População
- 5.2 Amostra
- 5.3 Variável
- 5.4 Medidas de tendência central
- 5.5 Medições de dispersão
- 6 tópicos de interesse
- 7 referências
História
Idade Antiga
A estatística tem sua origem na necessidade humana de organizar as informações necessárias à sua sobrevivência e bem-estar, bem como de se antecipar aos eventos que a afetam. As grandes civilizações da antiguidade deixaram registros de colonos, impostos recolhidos, quantidade de colheitas e tamanho dos exércitos..
Por exemplo, durante seu longo reinado, Ramsés II (1279-1213 aC) ordenou um censo das terras e habitantes do Egito, que então tinha cerca de 2 milhões de habitantes.
Da mesma forma, a Bíblia narra que Moisés realizou um censo para descobrir quantos soldados as doze tribos de Israel tinham.
Também na Grécia antiga, pessoas e recursos eram contados. Os romanos, notáveis por sua alta organização, registravam periodicamente a população, fazendo censos a cada cinco anos, incluindo territórios e recursos..
Renascimento
Após o declínio de Roma, registros estatísticos importantes eram escassos, até a chegada da Renascença, quando as estatísticas ressurgiram como um auxílio na tomada de decisões..
No final do século XVII, nasceu a teoria das probabilidades, fruto da inclinação das pessoas para os jogos de azar, o que conferiu à Estatística o rigor matemático que a tornou uma ciência por direito próprio..
Idade Moderna
Um novo impulso veio com a teoria dos erros e mínimos quadrados no século 19, que foi seguida pelo método de correlação entre variáveis, para avaliar quantitativamente a relação entre elas..
Até que finalmente, durante o século 20, a Estatística se espalhou para cada ramo da ciência e da engenharia como uma ferramenta indispensável na resolução de problemas..
Características de estatísticas descritivas
As estatísticas descritivas são caracterizadas por:
- Organize as informações coletadas na forma de dados e gráficos. Os gráficos podem ser diversos: histogramas, polígonos de frequência, diagramas em formato de pizza, entre outros..
- Distribua os dados em faixas de frequência para facilitar seu gerenciamento. Use aritmética para encontrar os valores mais representativos dos dados, por meio de medidas de tendência central, bem como para analisar sua dispersão.
- Determine a forma das distribuições, sua simetria, se estão centradas ou enviesadas e se são pontiagudas ou achatadas.
O que são estatísticas descritivas para?
Sempre que os dados precisam ser coletados, organizados e apresentados, as estatísticas descritivas são essenciais em áreas da ciência que lidam com muitos elementos e quantidades, bem como em muitas atividades humanas: economia, política, saúde, esportes e muito mais..
aqui estão alguns exemplos:
Economia
A estatística descritiva preocupa-se com o registro e a organização consistente de dados sobre populações e suas idades, renda, investimentos, ganhos e despesas. Dessa forma, governos e instituições planejam melhorias e investem recursos de forma adequada..
Com sua ajuda, são monitoradas compras, vendas, devoluções e eficiência dos serviços. Por esse motivo, as estatísticas são essenciais na tomada de decisões.
Física e Mecânica
A Física e a Mecânica usam a Estatística para estudar meios contínuos, que consistem em um grande número de partículas, como átomos e moléculas. Acontece que não é possível rastrear cada um deles separadamente..
Mas estudando o comportamento global do sistema (uma porção de gás, por exemplo) do ponto de vista macroscópico, é possível encontrar médias e definir variáveis macroscópicas para conhecer suas propriedades. Um exemplo disso é a teoria cinética dos gases.
Medicamento
É uma ferramenta imprescindível no monitoramento de doenças, desde suas origens e durante sua evolução, bem como a eficácia dos tratamentos..
As estatísticas que descrevem as taxas de morbidade, as taxas de cura, os tempos de incubação ou desenvolvimento de uma doença, a idade em que geralmente aparece e dados semelhantes são necessários ao projetar os tratamentos mais eficazes..
Nutrição
Uma das muitas aplicações da estatística descritiva é registrar e ordenar dados sobre o consumo de alimentos em diferentes populações: sua quantidade, qualidade e quais são os mais consumidos, entre tantas outras observações que interessam aos especialistas..
Exemplos de estatísticas descritivas
Aqui estão alguns exemplos que ilustram como as ferramentas de estatística descritiva são úteis para ajudar a tomar decisões:
Exemplo 1

As autoridades educacionais de um país planejam melhorias institucionais. Suponha que você vá implementar um novo sistema de cantina escolar.
Para isso, é necessário ter dados sobre a população estudantil, por exemplo, número de alunos por série, idade, sexo, altura, peso e nível socioeconômico. Essas informações são então apresentadas na forma de tabelas e gráficos..
Exemplo 2
Para acompanhar o time de futebol local e fazer novas contratações, os dirigentes acompanham o número de jogos disputados, vencidos, empatados e perdidos, bem como o número de gols, os marcadores e como eles conseguiram marcar: cobrança de falta, meia tribunal, penas, com perna esquerda ou direita, entre outros detalhes.
Exemplo 3
Uma sorveteria tem vários sabores de sorvete e quer melhorar suas vendas, por isso os proprietários realizam um estudo onde contam o número de clientes, os separam em grupos por sexo e faixa etária.
Neste estudo, são registrados o sabor de sorvete preferido e a apresentação do mais vendido, por exemplo. E com os dados coletados, eles planejam as compras dos sabores e dos recipientes e acessórios necessários ao seu preparo..
Noções básicas de estatística descritiva
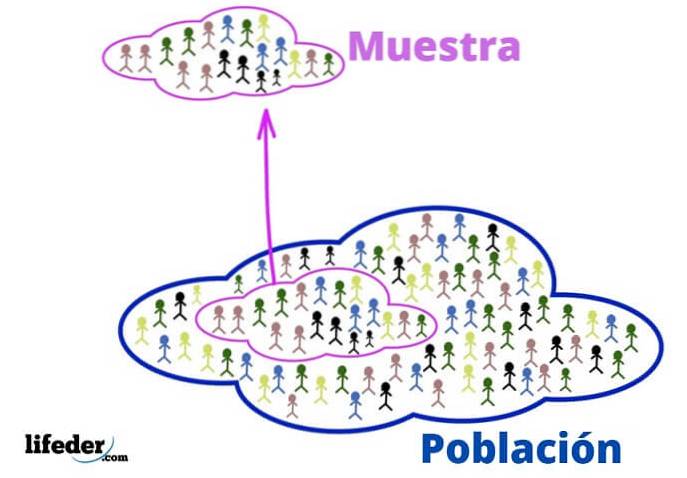
Esses conceitos fundamentais são necessários para aplicar técnicas estatísticas, vejamos:
População
No contexto estatístico, a população refere-se ao universo ou grupo de onde provém a informação.
Nem sempre são sobre pessoas, pois podem ser grupos de animais, plantas ou objetos como carros, átomos, moléculas e até eventos e ideias..
mostrar
Quando a população é muito grande, uma amostra representativa é retirada e analisada, sem perder informações relevantes..
Pode ser escolhido ao acaso, ou de acordo com alguns critérios previamente estabelecidos pelo analista. A vantagem é que sendo um subconjunto da população, é muito mais administrável.
Variável
Refere-se ao conjunto de valores que uma determinada característica da população pode assumir. Um estudo pode conter várias variáveis, como idade, sexo, peso, nível acadêmico, estado civil, renda, temperatura, cor, tempo e muito mais.
As variáveis podem ser de diferentes naturezas, por isso existem critérios para classificá-las e dar-lhes o tratamento mais adequado.
Variáveis categóricas e variáveis numéricas
Dependendo da forma como são medidas, as variáveis podem ser:
-Categórico
-Numérico
Variáveis categóricas, também chamadas qualitativo, representam qualidades como o estado civil de uma pessoa, que pode ser solteira, casada, divorciada ou viúva.
Em vez disso, variáveis numéricas ou quantitativo, pode ser medido, como idade, tempo, peso, renda e muito mais.
Variáveis discretas e variáveis contínuas
Variáveis discretas só aceitam valores discretos, como seu nome indica. Exemplos deles são o número de filhos em uma família, quantas disciplinas estão em um determinado curso e o número de carros em um estacionamento.
Essas variáveis nem sempre assumem valores inteiros, pois também existem valores fracionários.
Por outro lado, as variáveis contínuas admitem valores infinitos dentro de uma determinada faixa, como o peso de uma pessoa, o pH do sangue, o tempo de consulta telefônica e o diâmetro das bolas de futebol..
Medidas de tendência central
Eles dão uma ideia da tendência geral seguida pelos dados. Mencionaremos as três medidas centrais mais utilizadas:
-Metade
-Mediana
-moda
Metade
Equivalente à média dos valores. É calculado somando todas as observações e dividindo pelo número total:

moda
É o valor que mais se repete em um conjunto de dados, mais ou mais frequente, pois em uma distribuição pode haver mais de um modo.
Mediana
Ao classificar um conjunto de dados, a mediana é o valor central de todos eles.
Medidas de dispersão
Eles apontam a variabilidade dos dados e dão uma ideia de quão distantes ou dispersos estão das medidas centrais. Os mais usados são:
Classificação
É a diferença entre o maior valor xM e o menor xm de um conjunto de dados:
Classificação = xM - xm
Variância
Mede a distância entre os dados e o valor médio. Para fazer isso, é feita uma média, mas com as diferenças entre qualquer valor xeu e a média, quadrada para evitar que se anulem. Geralmente é denotado pela letra grega σ ao quadrado, ou com sdois:

A variância não tem as mesmas unidades dos dados, então o desvio padrão é definido como a raiz quadrada da variância e é denotado como σ ou s:

Em vez de levar em consideração cada dado individualmente, é preferível agrupá-los em faixas, o que facilita o trabalho, principalmente se houver muitos valores. Por exemplo, ao trabalhar com crianças em uma escola, elas podem ser agrupadas em faixas etárias: 0 a 6 anos, 6 a 12 anos e 12 a 18 anos.
Gráficos
Eles são uma ótima maneira de ver a distribuição dos dados em um piscar de olhos e contêm todas as informações coletadas nas tabelas e tabelas, mas muito mais acessíveis.
A variedade é grande: com barras, linear, circular, caule e folha, histogramas, polígonos de frequência e pictogramas. Exemplos de gráficos estatísticos são mostrados na Figura 3..
Assuntos de interesse
Ramos de estatísticas.
Variáveis estatísticas.
População e amostra.
Estatística inferencial.
Referências
- Faraldo, P. Estatística e Metodologia de Pesquisa. Recuperado de: eio.usc.es.
- Fernández, S. 2002. Estatísticas descritivas. 2ª Edição. Editorial da ESIC. Recuperado de: Google Livros.
- História da Estatística. Recuperado de: eumed.net.
- Ibañez, P. 2010. Mathematics II. Abordagem por competência. Cengage Learning.
- Monroy, S. 2008. Estatísticas descritivas. 1ª Edição. Instituto Politécnico Nacional do México.
- Fórmulas do universo. Estatística descritiva. Recuperado de: universoformulas.com.


Ainda sem comentários