
História da estatística inferencial, características, para que serve, exemplos

O Estatística inferencial ou estatística dedutiva é aquela que deduz as características de uma população a partir de amostras dela retiradas, por meio de uma série de técnicas de análise. Com as informações obtidas, são desenvolvidos modelos que permitem fazer previsões sobre o comportamento dessa população..
Por esse motivo, a estatística inferencial tornou-se a ciência número um por oferecer o suporte e os instrumentos que inúmeras disciplinas requerem na tomada de decisões..

Física, química, biologia, engenharia e ciências sociais se beneficiam continuamente dessas ferramentas quando criam seus modelos e projetam e implementam experimentos..
Índice do artigo
- 1 Breve história da estatística inferencial
- 1.1 Império Romano
- 1.2 Idade Média
- 1.3 Idade Moderna
- 1.4 Idade Contemporânea
- 2 recursos
- 3 Para que serve a estatística descritiva? Formulários
- 3.1 Sociologia e estudos demográficos
- 3.2 Engenharia
- 3.3 Economia e administração de empresas
- 4 Exemplos de estatística inferencial
- 4.1 Exemplo 1
- 4.2 Exemplo 2
- 5 conceitos básicos em estatística inferencial
- 5.1 Evento
- 5.2 Espaço de amostra
- 5.3 População e amostra
- 5.4 Amostragem
- 5.5 Variáveis estatísticas
- 5.6 Distribuições de probabilidade
- 5.7 Parâmetros e estatísticas
- 5.8 Hipótese estatística
- 5.9 Testes de hipóteses
- 6 tópicos de interesse
- 7 referências
Breve história da estatística inferencial
A estatística surgiu na antiguidade devido à necessidade das pessoas em organizar as coisas e otimizar recursos. Antes da invenção da escrita, eram feitos registros do número de pessoas e do gado disponível, por meio de símbolos gravados em pedra..
Posteriormente, os governantes chineses, babilônios e egípcios deixaram dados sobre a quantidade de safras e o número de habitantes, gravados em tabuletas de argila, colunas e monumentos..
Império Romano
Quando Roma exercia seu domínio no Mediterrâneo, era comum que as autoridades realizassem censos a cada cinco anos. Na verdade, a palavra "estatísticas" vem da palavra italiana statista, o que significa expressar.
Ao mesmo tempo, na América, os grandes impérios pré-colombianos também mantiveram registros semelhantes.
Idade Média
Durante a Idade Média, os governos da Europa, assim como a igreja, registraram a propriedade de terras. Em seguida, eles fizeram o mesmo com nascimentos, batismos, casamentos e mortes.
Idade Moderna
O estatístico inglês John Graunt (1620-1674) foi o primeiro a fazer previsões com base nessas listas, como quantas pessoas podem morrer de certas doenças e a proporção estimada de nascimentos de homens e mulheres. Por isso é considerado o pai da demografia..
Idade Contemporânea
Mais tarde, com o advento da teoria da probabilidade, a estatística deixou de ser uma mera coleção de técnicas organizacionais e alcançou um escopo insuspeitado como ciência preditiva..
Assim, os especialistas poderiam começar a desenvolver modelos de comportamento das populações e com eles deduzir o que coisas poderiam acontecer com pessoas, objetos e até mesmo ideias..
Caracteristicas

Abaixo, temos as características mais relevantes deste ramo da estatística:
- A estatística inferencial estuda uma população tirando dela uma amostra representativa.
- A seleção da amostra é realizada por meio de diversos procedimentos, sendo os mais adequados aqueles que escolhem os componentes de forma aleatória. Assim, qualquer elemento da população tem a mesma probabilidade de ser escolhido e, assim, vieses indesejados são evitados..
- Para organizar as informações coletadas faz uso de estatísticas descritivas.
- Variáveis estatísticas são calculadas na amostra que são usadas para estimar as propriedades da população..
- A estatística inferencial ou dedutiva faz uso da teoria da probabilidade para estudar eventos aleatórios, ou seja, aqueles que surgem fortuitamente. Cada evento é atribuído a uma certa probabilidade de ocorrência.
- Constrói hipóteses - suposições - sobre os parâmetros da população e os contrasta, para saber se estão corretos ou não, e também calcula o nível de confiança da resposta, ou seja, oferece uma margem de erro. O primeiro procedimento é chamado testando hipóteses, enquanto a margem de erro é o intervalo de confiança.
Para que serve a estatística descritiva? Formulários

Estudar uma população em sua totalidade pode exigir muitos recursos em dinheiro, tempo e esforço. É preferível obter amostras representativas que são muito mais gerenciáveis, coletar dados delas e criar hipóteses ou suposições sobre o comportamento da amostra.
Uma vez estabelecidas as hipóteses e testada sua validade, os resultados são estendidos à população e utilizados para a tomada de decisões..
Eles também ajudam a criar modelos dessa população, a fazer projeções para o futuro. É por isso que a estatística inferencial é uma ciência muito útil para:
Sociologia e estudos demográficos
Esses são campos ideais de aplicação, uma vez que as técnicas estatísticas são aplicadas com o objetivo de estabelecer vários modelos de comportamento humano. Algo que a priori é bastante complicado, pois inúmeras variáveis intervêm.
Na política, é muito utilizado em época eleitoral para conhecer a tendência eleitoral do eleitorado, desta forma os partidos traçam estratégias..
Engenharia
Os métodos da estatística inferencial são amplamente utilizados na Engenharia, sendo as aplicações mais importantes o controle de qualidade e a otimização de processos, por exemplo, melhorando os tempos de execução de tarefas, bem como prevenindo acidentes de trabalho..
Economia e administração de empresas
Com métodos dedutivos você pode realizar projeções sobre o funcionamento de uma empresa, o nível de vendas esperado, bem como auxiliar na tomada de decisões.
Por exemplo, suas técnicas podem ser utilizadas para estimar qual será a reação dos compradores a um novo produto, prestes a ser lançado no mercado..
Também serve para avaliar como estão as mudanças nos hábitos de consumo das pessoas, diante de eventos importantes, como a epidemia de COVID..
Exemplos de estatísticas inferenciais
Exemplo 1
Um problema de estatística dedutiva simples é o seguinte: um professor de matemática é responsável por 5 seções de álgebra elementar em uma universidade e decide usar as notas médias de uma só de suas seções para estimar a média de tudo.

Outra possibilidade é pegar uma amostra de cada seção, estudar suas características e estender os resultados a todas as seções..
Exemplo 2
O gerente de uma loja de roupas femininas quer saber quanto vai vender uma determinada blusa durante o verão. Para isso, analisa as vendas da peça durante as duas primeiras semanas da temporada e, assim, determina a tendência..
Conceitos básicos em estatística inferencial
Existem vários conceitos-chave, incluindo aqueles que vêm da teoria da probabilidade, sobre os quais você precisa ter clareza para entender o escopo completo dessas técnicas. Alguns, como população e amostra, já mencionamos ao longo do texto.
Evento
Um evento ou evento é algo que acontece e pode ter vários resultados. Um exemplo de um evento pode ser jogar uma moeda e há dois resultados possíveis: cara ou coroa.
Espaço amostral
É o conjunto de todos os resultados possíveis de um evento.
População e amostra
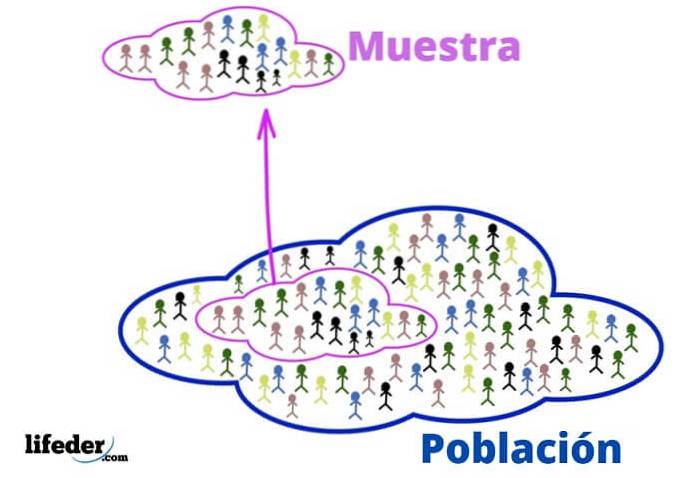
A população é o universo que você deseja estudar. Não se trata necessariamente de pessoas ou seres vivos, uma vez que a população, nas estatísticas, pode ser constituída por objetos ou ideias..
Por sua vez, a amostra é um subconjunto da população, dela cuidadosamente extraída por ser representativa..
Amostragem
É o conjunto de técnicas pelas quais uma amostra é selecionada de uma determinada população. A amostragem pode ser aleatória, se forem utilizados métodos probabilísticos para a escolha da amostra, ou não probabilística, se o analista tiver seus próprios critérios de seleção, de acordo com sua experiência..
Variáveis estatísticas
Conjunto de valores que podem ter as características da população. Eles são classificados de várias maneiras, por exemplo, podem ser discretos ou contínuos. Além disso, tendo em conta a sua natureza, podem ser qualitativos ou quantitativos..
Distribuições de probabilidade
Funções de probabilidade que descrevem o comportamento de um grande número de sistemas e situações observadas na natureza. As mais conhecidas são a distribuição do sino gaussiano ou gaussiano e a distribuição binomial.
Parâmetros e estatísticas
A teoria da estimação estabelece que existe uma relação entre os valores da população e os da amostra retirada dessa população. O parametros são as características da população que não sabemos, mas queremos estimar: por exemplo, a média e o desvio padrão.
Por sua parte, Estatisticas são as características da amostra, por exemplo, sua média e desvio padrão.
A título de exemplo, suponha que a população seja composta por todos os jovens entre 17 e 30 anos de uma comunidade, e queremos saber a proporção dos que estão atualmente cursando o ensino superior. Este seria o parâmetro da população para determinar.
Para estimá-lo, é selecionada uma amostra aleatória de 50 jovens e calculada a proporção deles que estudam em uma universidade ou instituto de ensino superior. Esta proporção é a estatística.
Se após o estudo for constatado que 63% dos 50 jovens estão cursando o ensino superior, esta é a estimativa populacional, feita a partir da amostra.
Este é apenas um exemplo do que a estatística inferencial pode fazer. É conhecido como estimativa, mas também existem técnicas para prever variáveis estatísticas, bem como para tomar decisões..
Hipótese estatística
É uma conjectura que se faz a respeito do valor da média e do desvio padrão de alguma característica da população. A menos que a população seja totalmente examinada, esses são valores desconhecidos.
Testando hipóteses
As suposições feitas sobre os parâmetros da população são válidas? Para descobrir, verifica-se se os resultados da amostra os suportam ou não, por isso é necessário desenhar testes de hipóteses..
Estas são as etapas gerais para realizar um:
Passo 1
Identifique o tipo de distribuição que se espera que a população siga.
Passo 2
Declare duas hipóteses, denotadas como Hou e H1. O primeiro é o hipótese nula em que assumimos que o parâmetro tem um determinado valor. O segundo é a hipótese alternativa que assume um valor diferente da hipótese nula. Se isso for rejeitado, então a hipótese alternativa é aceita.
etapa 3
Estabeleça uma margem aceitável para a diferença entre o parâmetro e a estatística. Raramente eles serão idênticos, embora se espere que sejam muito próximos..
Passo 4
Proponha um critério para aceitar ou rejeitar a hipótese nula. Para isso, é utilizada uma estatística de teste, que pode ser a média. Se o valor médio está dentro de certos limites, a hipótese nula é aceita, caso contrário, é rejeitada.
Etapa 5
Como etapa final, é decidido se aceita ou não a hipótese nula..
Assuntos de interesse
Ramos de estatísticas.
Variáveis estatísticas.
População e amostra.
Estatística descritiva.
Referências
- Berenson, M. 1985. Statistics for Management and Economics, Concepts and Applications. Editorial Interamericana.
- Canavos, G. 1988. Probabilidade e Estatística: Aplicações e métodos. Colina Mcgraw.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8º. Edição. Cengage Learning.
- História da Estatística. Recuperado de: eumed.net.
- Ibañez, P. 2010. Mathematics II. Abordagem por competência. Cengage Learning.
- Levin, R. 1981. Statistics for Administrators. Prentice Hall.
- Walpole, R. 2007. Probabilidade e Estatística para Engenharia e Ciências. Pearson.


Ainda sem comentários