
Medições experimentais de Torricelli de pressão atmosférica, importância
O Experimento de Torricelli Foi realizada pelo físico e matemático italiano Evangelista Torricelli em 1644 e resultou na primeira medição da pressão atmosférica..
Esta experiência surgiu da necessidade de melhorar o abastecimento de água nas cidades. Evangelista Torricelli (1608-1647), que era um matemático da corte do Grão-duque da Toscana Fernando II, havia estudado fenômenos hidráulicos junto com Galileu.
Índice do artigo
- 1 o experimento
- 2 A medição da pressão atmosférica
- 2.1 O barômetro Torricelli
- 3 Importância da pressão atmosférica para o clima
- 3.1 Torr e outras unidades de pressão
- 3.2 Altímetros
- 4 referências
O experimento
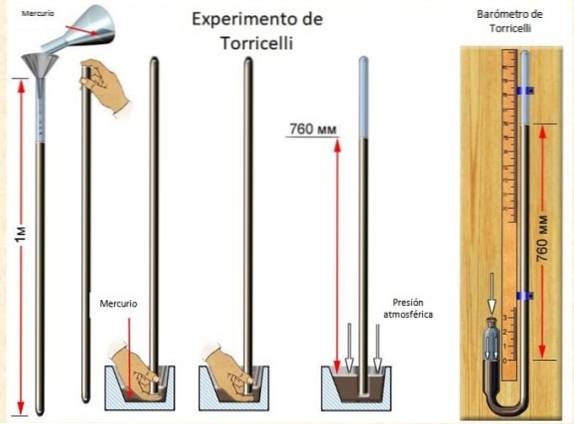
Em 1644, Torricelli fez a seguinte experiência:
- Ele introduziu o mercúrio em um tubo de 1 m de comprimento, aberto em uma extremidade e fechado na outra..
- Quando o tubo estava completamente cheio, ele o inverteu e jogou em um recipiente que também continha mercúrio..
- Torricelli observou que a coluna desceu e parou a cerca de 76 cm de altura.
- Ele também percebeu que um vácuo foi criado no espaço que era livre, embora não perfeito..
Torricelli repetiu a experiência usando tubos diferentes. Ele até fez uma pequena variação: colocou água no balde, que, por ser mais leve, flutuava no mercúrio. Em seguida, ele levantou lentamente o tubo contendo mercúrio até a superfície da água..
Então o mercúrio desceu e a água subiu. O vácuo obtido, como já dissemos, não foi perfeito, pois sempre houve resquícios de vapor de mercúrio ou água..
A medição da pressão atmosférica
A atmosfera é uma mistura de gases em que predominam o nitrogênio e o oxigênio, com vestígios de outros gases como argônio, dióxido de carbono, hidrogênio, metano, monóxido de carbono, vapor d'água e ozônio..
A atração gravitacional exercida pela Terra é responsável por manter todo o entorno do planeta.
Claro, a composição não é uniforme, nem a densidade, pois depende da temperatura. Perto da superfície existe uma boa quantidade de poeira, areia e poluentes de eventos naturais e também da atividade humana. As moléculas mais pesadas estão mais próximas do solo.
Como há tanta variabilidade, é necessário escolher uma altitude de referência para a pressão atmosférica, que por conveniência foi tomada como nível do mar..
Aqui não é qualquer nível do mar, porque também apresenta oscilações. O nível o dado um sistema de referência geodésico é escolhido com a ajuda de um acordo comum entre os especialistas.
Quanto vale a pressão atmosférica perto do solo? Torricelli encontrou seu valor ao medir a altura da coluna: 760 mm de mercúrio.
O barômetro Torricelli
No topo do tubo, a pressão é 0, pois o vácuo foi estabelecido ali. Enquanto isso, na superfície da cuba de mercúrio, a pressão P1 é a pressão atmosférica.
Vamos escolher a origem do referencial na superfície livre do mercúrio, na parte superior do tubo. A partir daí, até a superfície do mercúrio no recipiente ser medida H, a altura da coluna.
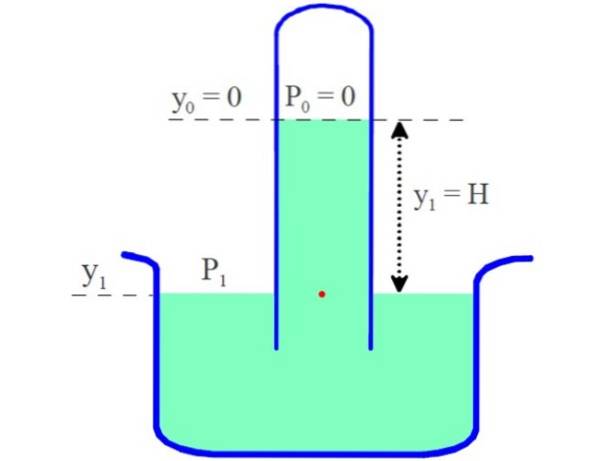
A pressão no ponto marcado em vermelho, na profundidade e1 isso é:
P1 = Pou + ρHg . g.y1
Onde ρHg é a densidade do mercúrio. Sendo que Y1 = H Y Po = 0:
P1 = ρHg . g.H
H = P1/ ρHg.g
Uma vez que a densidade do mercúrio é constante e a gravidade é constante, verifica-se que a altura da coluna de mercúrio é proporcional a P1, que é a pressão atmosférica. Substituindo valores conhecidos:
H = 760 mm = 760 x 10 -3 m
g = 9,8 m / sdois
ρHg = 13,6 g / cc = 13,6 x 10 3 kg / m3
P1 = 13,6 x 10 3 kg / m3 x 9,8 m / sdois x 760 x 10 -3 m = 101,293 N / mdois= 101,3 kN / mdois
A unidade de pressão no Sistema Internacional é o pascal, abreviado Pa. De acordo com o experimento de Torricelli, a pressão atmosférica é 101,3 kPa.
Importância da pressão atmosférica para o clima
Torricelli observou que o nível de mercúrio no tubo sofria pequenas variações a cada dia, então ele deduziu que a pressão atmosférica também deve mudar..
A pressão atmosférica é responsável por grande parte do clima, porém suas variações diárias passam despercebidas. É porque eles não são tão perceptíveis quanto tempestades ou frio, por exemplo.
No entanto, essas variações na pressão atmosférica são responsáveis pelos ventos, que por sua vez influenciam as chuvas, a temperatura e a umidade relativa. Quando o solo aquece, o ar se expande e tende a subir, fazendo com que a pressão caia.
Sempre que o barômetro indica altas pressões, pode-se esperar bom tempo, enquanto que com baixas pressões existe a possibilidade de tempestades. No entanto, para fazer previsões precisas do clima, é necessário ter mais informações sobre outros fatores..
O torr e outras unidades para pressão
Embora pareça estranho, já que a pressão é definida como força por unidade de área, em meteorologia é válido expressar a pressão atmosférica em milímetros de mercúrio, conforme estabelecido por Torricelli.
É porque o barômetro de mercúrio continua a ser usado hoje com pouca variação desde aquela época, de forma que em homenagem a Torricelli, 760 mm de Hg é igual a 1 torr. Em outras palavras:
1 torr = 760 mm Hg = 30 polegadas de Hg = 1 pressão atmosférica = 101,3 kPa
Se Torricelli tivesse usado água em vez de mercúrio, a altura da coluna seria de 10,3 m. O barômetro de mercúrio é mais prático por ser mais compacto.
Outras unidades amplamente utilizadas são barras e milibares. Um milibar equivale a um hectopascal ou 10dois pascal.
Altímetros
Um altímetro é um instrumento que indica a altura de um local, comparando a pressão atmosférica naquela altura com a do solo ou outro ponto de referência.
Se a altura não for muito grande, em princípio podemos supor que a densidade do ar permanece constante. Mas esta é uma aproximação, pois sabemos que a densidade da atmosfera diminui com a altura.
Usando a equação usada acima, a densidade do ar é usada em vez da do mercúrio:
P1 = Pou + ρar . g.H
Nesta expressão Pou é tomada como a pressão atmosférica ao nível do solo e P1 é aquele do lugar cuja altitude deve ser determinada:
H = (P1 - Pou) / ρar . g

A equação altimétrica mostra que a pressão diminui exponencialmente com a altura: para H = 0, P1= Pou e sim H → ∞, então P1=0.
Referências
- Figueroa, D. 2005. Série: Física para Ciências e Engenharia. Volume 5. Fluidos e termodinâmica. Editado por Douglas Figueroa (USB).
- Kirkpatrick, L. 2007. Physics: A Look at the World. 6ª edição resumida. Cengage Learning.
- Lay, J. 2004. General Physics for Engineers. USACH.
- Mott, R. 2006. Mecânica dos fluidos. 4º. Edição. Pearson Education.
- Strangeways, I. 2003. Measuring the Natural Environment. 2ª Edição. Cambridge University Press.


Ainda sem comentários