Fluxo de campo elétrico

O que é fluxo de campo elétrico?

O fluxo de campo elétrico ou simplesmente fluxo elétrico é uma quantidade escalar proporcional ao número de linhas de campo elétrico que passam por uma superfície. É denotado pela letra grega maiúscula Φ (phi).

O campo elétrico na verdade não "flui" da maneira que um fluxo de água, embora as linhas do fluido se assemelhem às do campo elétrico..

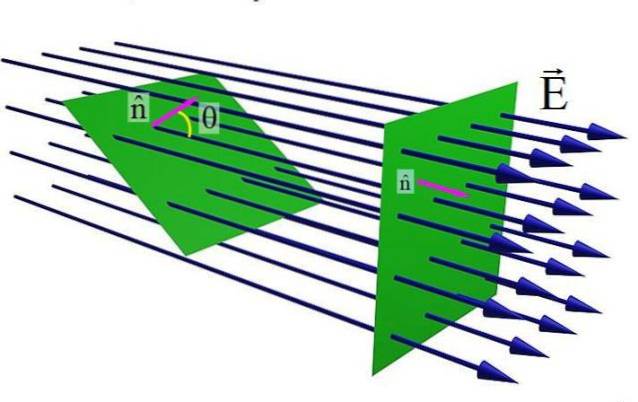
A figura acima mostra uma superfície plana atravessada por um campo elétrico E. Quando o vetor unitário normal à superfície n e o campo E são paralelas, o número de linhas de campo que cruzam a superfície é máximo. Mas como o ângulo θ entre n Y E, o número de linhas que passam pela superfície verde é menor.

Por outro lado, o fluxo do campo elétrico também depende da magnitude do E, porque quanto maior, mais linhas de campo cruzam a superfície. E, claro, quanto maior a área S da referida superfície, maior será o fluxo, então a seguinte equação é estabelecida:

Φ = E ∙ Scosθ

Esta expressão é consistente com o produto escalar entre os vetores E Y n:

Φ = (E • n) S

A unidade para fluxo de campo elétrico no Sistema Internacional de Unidades SI é N.m^dois/ C (newton x metro quadrado / coulomb). Alternativamente, uma vez que o campo também é medido em V / m (volt sobre medidor), o fluxo elétrico permanece em (V ∙ m).

Exemplos

De acordo com a definição, o fluxo elétrico pode ser positivo, negativo ou igual a 0. O fluxo do campo elétrico é:

-Positivo quando o ângulo θ entre E Y n é menor que 90º, uma vez que cos θ é maior que zero.

-Negativo se o referido ângulo for maior que 90º, porque então cos θ é menor que zero.

-Nulo quando θ é exatamente 90º, porque cos 90º = 0 e as linhas de campo neste caso são tangenciais à superfície.

-Por outro lado, se o ângulo entre E Y n é igual a 0, o fluxo adquire seu valor máximo.

Essas possibilidades são mostradas na imagem a seguir:

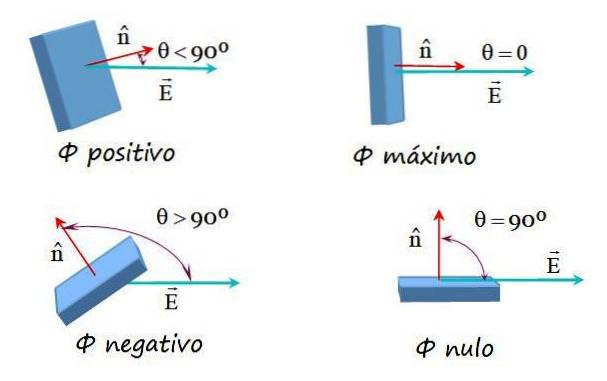
Fluxo de campo elétrico em uma superfície arbitrária

Anteriormente, o fluxo do campo elétrico era determinado no caso particular de um incidente de campo uniforme em uma superfície plana. Para uma superfície de forma S arbitrária e / ou um campo elétrico não uniforme, o ângulo entre E Y n pode variar de ponto a ponto.

Na figura a seguir há dois exemplos, à esquerda uma superfície curva e à direita uma superfície fechada.

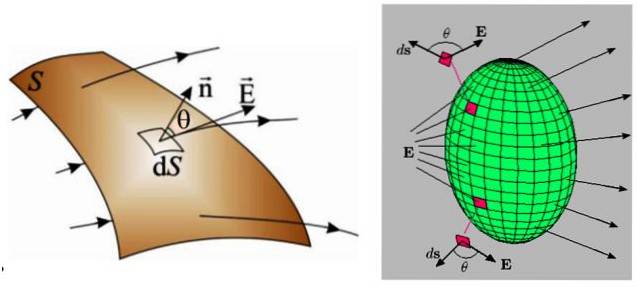
Em ambos os casos, a superfície é dividida em regiões muito menores, de tamanho infinitesimal, chamadas dS, por onde passa um fluxo também dΦ infinitesimal:

dΦ = (E•n) dS = (Ecosθ) dS

O campo total é obtido pela adição de todas essas contribuições infinitesimais:

No caso de superfícies fechadas, n sempre aponta para fora, pois o fluxo tem um sinal + quando é saliente para S, uma vez que o ângulo entre E Y n é menor que 90º, e sinal - quando o campo está entrando, porque então o ângulo entre E Y n é maior que 90º (ver figura 2).

Observe que na superfície fechada à direita, o número de linhas de campo que entram na superfície é igual ao número de linhas que saem. Portanto, o fluxo líquido, definido como a soma algébrica do fluxo de entrada e do fluxo de saída, é zero.

A fonte do campo elétrico neste caso está fora da superfície, entretanto, o fluxo líquido seria diferente de 0 se a fonte do campo elétrico (a distribuição de cargas) estivesse dentro da superfície..

Treinamento

Exercício 1

Tem um campo elétrico E = 3,5 kN / C x e uma superfície plana retangular de 0,35 m de largura por 0,7 m de comprimento. Encontre o fluxo do campo elétrico através do retângulo nos seguintes casos:

a) A superfície é paralela ao plano yz.

b) O retângulo é paralelo ao plano xy.

c) A normal do plano forma um ângulo de 40º com o eixo x e contém o eixo y.

Solução para

O vetor normal e o vetor campo elétrico são paralelos, portanto o ângulo θ entre eles é 0º e o fluxo elétrico é:

Φ = (E ∙ S) cos 0 = E ∙ S

A área S do retângulo é:

S = 0,35 m x 0,7 m = 0,245 m^dois

Substituindo em Φ:

Φ = E ∙ S = 3,5 x 10³ N / C × 0,245 m^dois = 857,5 N ∙ m^dois / C.

Solução b

O fluxo do campo elétrico é 0, uma vez que os vetores E Y n são perpendiculares entre si.

Solução c

O ângulo θ entre o campo E e o vetor normal n é 40º (ver figura), portanto:

Φ = E ∙ S ∙ cos θ = 3,5 x 10³ N / C × 0,245 m^dois × cos 40º = 656,9 N ∙ m^dois / C.

Exercício 2

Calcule o fluxo do campo elétrico que produz uma carga pontual positiva q_ou = 2μC localizado no centro de uma esfera de raio R = 5 cm.

Solução

O campo produzido pela carga q_ou Não é uniforme, mas pela lei de Coulomb sabe-se que na superfície da esfera tem magnitude de:

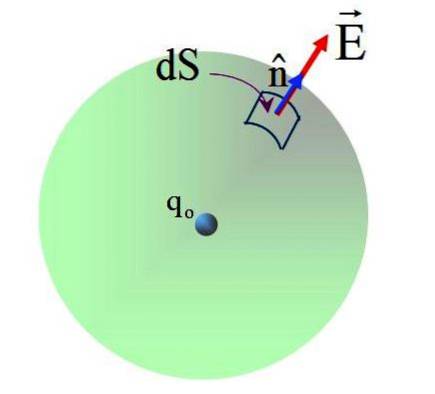
O campo tem uma direção radial, e o vetor normal n, portanto, o ângulo entre os dois vetores é 0 em todos os pontos da superfície esférica. Substituindo em:

Se tem que:

A integral de dS sobre toda a superfície esférica S é sua área, que é 4πR^dois, portanto:

Seu valor é:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m^dois/ C = 2,3 x 10⁵ N⋅m^dois/ C

Referências

1. Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill.
2. Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 5. Eletrostática. Editado por Douglas Figueroa (USB).
3. Giambattista, A. 2010. Física. 2ª Ed. McGraw Hill.
4. Giancoli, D. 2006. Física: Princípios com Aplicações. 6º. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Física Universitária com Física Moderna. 14º. Ed. Volume 1. Pearson.