
Casos e exemplos de frações parciais
As Frações Parciais são frações formadas por polinômios, em que o denominador pode ser um polinômio linear ou quadrático e, além disso, pode ser elevado a alguma potência. Às vezes, quando temos funções racionais, é muito útil reescrever essa função como uma soma de frações parciais ou frações simples..
Isto porque desta forma podemos manipular melhor estas funções, especialmente nos casos em que é necessário integrar a referida aplicação. Uma função racional é simplesmente o quociente entre dois polinômios, e eles podem ser próprios ou impróprios.

Se o grau do polinômio do numerador for menor que o denominador, é chamada de função racional própria; caso contrário, é conhecido como uma função racional imprópria.
Índice do artigo
- 1 definição
- 2 casos
- 2.1 Caso 1
- 2.2 Caso 2
- 2.3 Caso 3
- 2.4 Caso 4
- 3 aplicativos
- 3.1 Cálculo Integral
- 3.2 Lei de ação em massa
- 3.3 Equações diferenciais: equação logística
- 4 referências
Definição
Quando temos uma função racional imprópria, podemos dividir o polinômio do numerador pelo polinômio do denominador e assim reescrever a fração p (x) / q (x), seguindo o algoritmo de divisão como t (x) + s (x ) / q (x), onde t (x) é um polinômio e s (x) / q (x) é uma função racional adequada.
Uma fração parcial é qualquer função própria de polinômios, cujo denominador tem a forma (ax + b)n o (machadodois+ bx + c)n, se o machado polinomialdois + bx + c não tem raízes reais en é um número natural.
Para reescrever uma função racional em frações parciais, a primeira coisa a fazer é fatorar o denominador q (x) como um produto de fatores lineares e / ou quadráticos. Feito isso, passamos a determinar as frações parciais, que dependem da natureza desses fatores..
Estojos
Nós consideramos vários casos separadamente.
Caso 1
Os fatores de q (x) são todos lineares e nenhum se repete. Quer dizer:
q (x) = (a1x + b1) (paradoisx + bdois)… (parasx + bs)
Nenhum fator linear é idêntico a outro. Quando este caso ocorrer, escreveremos:
p (x) / q (x) = A1/(para1x + b1) + Adois/(paradoisx + bdois)… + As/(parasx + bs).
Para onde1,PARAdois,… ,PARAs são as constantes que você deseja encontrar.
Exemplo
Queremos decompor a função racional em frações simples:
(x - 1) / (x3+3xdois+2x)
Passamos a fatorar o denominador, ou seja:
x3 + 3xdois + 2x = x (x + 1) (x + 2)
Mais tarde:
(x - 1) / (x3+3xdois+2x) = (x - 1) / x (x + 1) (x + 2)
(x - 1) / x (x + 1) (x + 2) = A / x + B / (x + 1) + C / (x + 2)
Aplicando o mínimo múltiplo comum, pode-se obter que:
x - 1 = A (x + 1) (x + 2) + B (x + 2) x + C (x + 1) x.
Queremos obter os valores das constantes A, B e C, que podem ser encontrados substituindo as raízes que cancelam cada um dos termos. Substituindo 0 por x, temos:
0 - 1 = A (0 + 1) (0 + 2) + B (0 + 2) 0 + C (0 + 1) 0.
- 1 = 2A
A = - 1/2.
Substituindo - 1 por x, temos:
- 1 - 1 = A (- 1 + 1) (- 1 + 2) + B (- 1 + 2) (- 1) + C (- 1 + 1) (- 1).
- 2 = - B
B = 2.
Substituindo - 2 por x, temos:
- 2 - 1 = A (- 2 + 1) (- 2 + 2) + B (- 2 + 2) (- 2) + C (- 2 + 1) (- 2).
-3 = 2C
C = -3/2.
Desta forma, os valores A = -1/2, B = 2 e C = -3/2 são obtidos.
Existe outro método para obter os valores de A, B e C. Se no lado direito da equação x - 1 = A (x + 1) (x + 2) + B (x + 2) x + C (x + 1) x combinamos termos, temos:
x - 1 = (A + B + C) xdois + (3A + 2B + C) x + 2A.
Como se trata de uma igualdade de polinômios, temos que os coeficientes do lado esquerdo devem ser iguais aos do lado direito. Isso resulta no seguinte sistema de equações:
A + B + C = 0
3A + 2B + C = 1
2A = - 1
Resolvendo este sistema de equações, obtemos os resultados A = -1/2, B = 2 e C = -3/2.
Por fim, substituindo os valores obtidos temos que:
(x - 1) / x (x + 1) (x + 2) = - 1 / (2x) + 2 / (x + 1) - 3 / (2 (x + 2)).
Caso 2
Os fatores de q (x) são todos lineares e alguns se repetem. Suponha que (ax + b) seja um fator que se repete vezes “s”; então, a este fator corresponde a soma das frações parciais "s".
PARAs/ (ax + b)s + PARAs-1/ (ax + b)s-1 +… + A1/ (ax + b).
Onde o As,PARAs-1,… , PARA1 são as constantes a serem determinadas. Com o exemplo a seguir, mostraremos como determinar essas constantes.
Exemplo
Decompor em frações parciais:
(x - 1) / (xdois(x - 2)3)
Escrevemos a função racional como uma soma de frações parciais da seguinte forma:
(x - 1) / (xdois(x - 2)3) = A / xdois + B / x + C / (x - 2)3 + D / (x - 2)dois + E / (x - 2).
Mais tarde:
x - 1 = A (x - 2)3 + B (x - 2)3x + Cxdois + D (x - 2) xdois + E (x - 2)doisxdois
Substituindo 2 por x, temos que:
7 = 4C, ou seja, C = 7/4.
Substituindo 0 por x, temos:
- 1 = -8A ou A = 1/8.
Substituindo esses valores na equação anterior e desenvolvendo, temos que:
x - 1 = 1/8 (x3 - 6xdois + 12x - 8) + Bx (x3 - 6xdois + 12x - 8) + 7 / 4xdois +Dx3 - 2Dxdois + Antigodois(xdois - 4x + 4)
x - 1 = (B + E) x4 + (1/8 - 6B + D - 4E) x3 + (- ¾ + 12B + 7/4 - 2D + 4E) xdois +(3/2 - 8B) x - 1.
Equacionando os coeficientes, obtemos o seguinte sistema de equações:
B + E = 0;
1 / 8-6B + D-4E = 1;
- 3/4 + 12B + 7/4 - 2D + 4E = 0
3/2 - 8B = 0.
Resolvendo o sistema, temos:
B = 3/16; D = 5/4; E = - 3/16.
Para isso, temos que:
(x - 1) / (xdois(x - 2)3) = (1/8) / xdois + (3/16) / x + (7/4) / (x - 2)3 + (5/4) / (x - 2)dois - (3/16) / (x - 2).
Caso 3
Os fatores de q (x) são quadráticos lineares, sem quaisquer fatores quadráticos repetidos. Para este caso, o fator quadrático (machadodois + bx + c) corresponderá à fração parcial (Ax + B) / (axdois + bx + c), onde as constantes A e B são aquelas que queremos determinar.
O exemplo a seguir mostra como proceder neste caso
Exemplo
Decompor em frações simples a (x + 1) / (x3 - 1).
Primeiro, passamos a fatorar o denominador, o que nos dá o resultado:
(x - 1) = (x - 1) (x + x +1).
Podemos observar que (xdois + x + 1) é um polinômio quadrático irredutível; ou seja, não tem raízes reais. Sua decomposição em frações parciais será a seguinte:
(x + 1) / (x - 1) (xdois + x +1) = A / (x - 1) + (Bx + C) / (xdois + x +1)
A partir disso, obtemos a seguinte equação:
x + 1 = (A + B) xdois +(A - B + C) x + (A - C)
Usando a igualdade de polinômios, obtemos o seguinte sistema:
A + B = 0;
AB + C = 1;
A-C = 1;
Deste sistema, temos que A = 2/3, B = - 2/3 e C = 1/3. Substituindo, temos que:
(x + 1) / (x - 1) (xdois + x +1) = 2/3 (x - 1) - (2x + 1) / 3 (xdois + x +1).
Caso 4
Finalmente, o caso 4 é aquele em que os fatores de q (x) são lineares e quadráticos, onde alguns dos fatores quadráticos lineares se repetem.
Neste caso, if (axdois + bx + c) é um fator quadrático que se repete “s” vezes, então a fração parcial correspondente ao fator (axdois + bx + c) será:
(PARA1x + B) / (machadodois + bx + c) +… + (As-1x + Bs-1) / (machadodois + bx + c)s-1 + (PARAsx + Bs) / (machadodois + bx + c)s
Onde o As, PARAs-1,…, A e Bs, Bs-1,..., B são as constantes a serem determinadas.
Exemplo
Queremos decompor a seguinte função racional em frações parciais:
(x - 2) / (x (xdois - 4x + 5)dois)
Como xdois - 4x + 5 é um fator quadrático irredutível, temos que sua decomposição em frações parciais é dada por:
(x - 2) / (x (xdois - 4x + 5)dois) = A / x + (Bx + C) / (xdois - 4x +5) + (Dx + E) / (xdois - 4x + 5)dois
Simplificando e desenvolvendo, ficamos com:
x - 2 = A (xdois - 4x + 5)dois + (Bx + C) (xdois - 4x + 5) x + (Dx + E) x
x - 2 = (A + B) x4 + (- 8A - 4B + C) x3 + (26A + 5B - 4C + D) xdois + (- 40A + 5C + E) x + 25A.
Do exposto, temos o seguinte sistema de equações:
A + B = 0;
- 8A - 4B + C = 0;
26A + 5B - 4C + D = 0;
- 40A + 5C + E = 1;
25A = 2.
Ao resolver o sistema, ficamos com:
A = - 2/25, B = 2/25, C = - 8/25, D = 2/5 e E = - 3/5.
Substituindo os valores obtidos temos:
(x - 2) / (x (xdois - 4x + 5)dois) = -2 / 25x + (2x - 8) / 25 (xdois - 4x +5) + (2x - 3) / 5 (xdois - 4x + 5)dois
Formulários
Cálculo integral
As frações parciais são usadas principalmente para o estudo do cálculo integral. A seguir, veremos alguns exemplos de como realizar integrais usando frações parciais.
Exemplo 1
Queremos calcular a integral de:
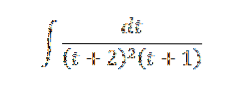
Podemos ver que o denominador q (x) = (t + 2)dois(t + 1) é composto de fatores lineares onde um deles é repetido; é por isso que estamos no caso 2.
Temos que:
1 / (t + 2)dois(t + 1) = A / (t + 2)dois +B / (t + 2) + C / (t + 1)
Reescrevemos a equação e temos:
1 = A (t + 1) + B (t + 2) (t + 1) + C (t + 2)dois
Se t = - 1, temos:
1 = A (0) + B (1) (0) + C (1)
1 = C
Se t = - 2, isso nos dá:
1 = A (- 1) + B (0) (- 1) + C (0)
A = - 1
Então, se t = 0:
1 = A (1) + B (2) (1) + C (2)
Substituindo os valores de A e C:
1 = - 1 + 2B + 4
1 = 3 + 2B
2B = - 2
Do exposto, temos que B = - 1.
Reescrevemos a integral como:
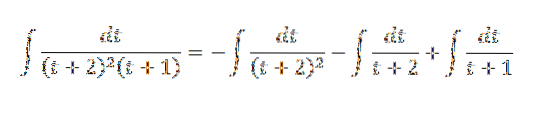
Prosseguimos para resolvê-lo pelo método de substituição:
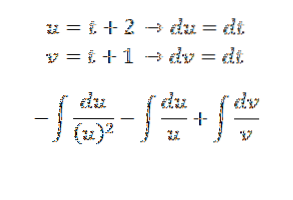
Este é o resultado:
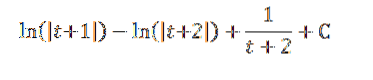
Exemplo 2
Resolva o seguinte integral:

Neste caso, podemos fatorar para q (x) = xdois - 4 como q (x) = (x - 2) (x + 2). Estamos claramente no caso 1. Portanto:
(5x - 2) / (x - 2) (x + 2) = A / (x - 2) + B / (x + 2)
Também pode ser expresso como:
5x - 2 = A (x + 2) + B (x - 2)
Se x = - 2, temos:
- 12 = A (0) + B (- 4)
B = 3
E se x = 2:
8 = A (4) + B (0)
A = 2
Assim, resta-nos resolver a integral dada é equivalente a resolver:
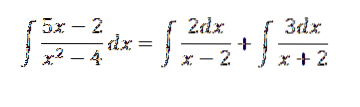
Isso nos dá como resultado:
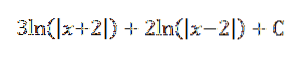
Exemplo 3
Resolva o integral:
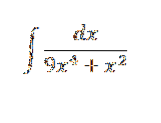
Temos q (x) = 9x4 + xdois , que podemos fatorar em q (x) = xdois(9xdois + 1).
Desta vez, temos um fator linear repetido e um fator quadrático; ou seja, estamos no caso 3.
Temos que:
1 / xdois(9xdois + 1) = A / xdois + B / x + (Cx + D) / (9xdois + 1)
1 = A (9xdois + 1) + Bx (9xdois + 1) + Cxdois + Dxdois
Agrupando e usando polinômios iguais, temos:
1 = (9B + C) x + (9A + D) x + Bx + A
A = 1;
B = 0;
9A + D = 0;
9B + C = 0
A partir deste sistema de equações, temos:
D = - 9 e C = 0
Desta forma, temos:
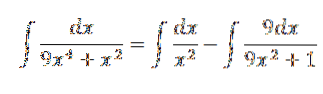
Ao resolver o acima, temos:
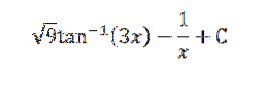
Lei da ação em massa
Uma aplicação interessante das frações parciais aplicadas ao cálculo integral é encontrada na química, mais precisamente na lei de ação de massa..
Suponha que temos duas substâncias, A e B, que se unem e formam uma substância C, de modo que a derivada da quantidade de C em relação ao tempo é proporcional ao produto das quantidades de A e B em qualquer momento.
Podemos expressar a lei da ação em massa da seguinte forma:
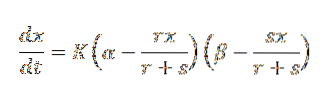
Nesta expressão α é o número inicial de gramas correspondendo a A e β o número inicial de gramas correspondendo a B.
Além disso, r e s representam o número de gramas de A e B respectivamente que se combinam para formar r + s gramas de C. Por sua vez, x representa o número de gramas da substância C no tempo t, e K é a constante de proporcionalidade . Podemos reescrever a equação acima como:

Fazendo a seguinte mudança:

Temos que a equação se torna:

A partir desta expressão podemos obter:
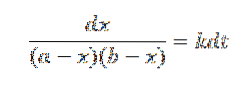
Onde se a ≠ b, frações parciais podem ser usadas para integração.
Exemplo
Tomemos por exemplo uma substância C que surge da combinação de uma substância A com a B, de forma que a lei da massa seja cumprida onde os valores de aeb são 8 e 6 respectivamente. Dê uma equação que nos dê o valor de gramas de C em função do tempo.
Substituindo os valores na lei de massa dada, temos:

Ao separar as variáveis, temos:

Aqui 1 / (8 - x) (6 - x) pode ser escrito como a soma das frações parciais, como segue:
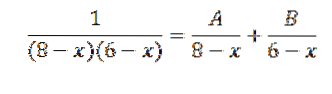
Assim, 1 = A (6 - x) + B (8 - x)
Se substituirmos 6 por x, teremos B = 1/2; e substituindo 8 por x, temos A = - 1/2.
Integrando por frações parciais, temos:

Isso nos dá como resultado:

Equações diferenciais: equação logística
Outra aplicação que pode ser dada às frações parciais é na equação diferencial logística. Em modelos simples, temos que a taxa de crescimento de uma população é proporcional ao seu tamanho; quer dizer:
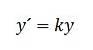
Esse caso é um ideal e é considerado realista até que os recursos disponíveis em um sistema sejam insuficientes para o sustento da população..
Nessas situações, o mais razoável é pensar que existe uma capacidade máxima, que chamaremos de L, que o sistema pode sustentar e que a taxa de crescimento é proporcional ao tamanho da população multiplicado pelo tamanho disponível. Este argumento leva à seguinte equação diferencial:
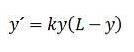
Essa expressão é chamada de equação diferencial logística. É uma equação diferencial separável que pode ser resolvida com o método de integração de fração parcial.
Exemplo
Um exemplo seria considerar uma população que cresce de acordo com a seguinte equação diferencial logística y '= 0,0004y (1000 - y), cujos dados iniciais são 400. Queremos saber o tamanho da população no momento t = 2, onde t é medido em anos.
Se escrevermos y 'com a notação de Leibniz como uma função que depende de t, temos:

A integral no lado esquerdo pode ser resolvida usando o método de integração da fração parcial:
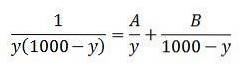
Podemos reescrever esta última igualdade da seguinte maneira:
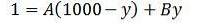
- Substituindo y = 0 temos que A é igual a 1/1000.
- Substituindo y = 1000, temos que B é igual a 1/1000.
Com esses valores, a integral é a seguinte:
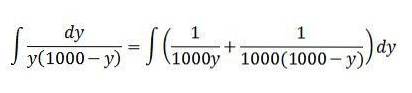
A solução é:

Usando os dados iniciais:

Ao limpar e temos:

Então temos isso em t = 2:
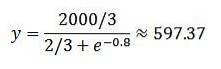
Em conclusão, após 2 anos, o tamanho da população é de aproximadamente 597,37.
Referências
- A, R. A. (2012). Matemática 1. Universidade dos Andes. Conselho de Publicações.
- Cortez, I., & Sanchez, C. (s.f.). 801 Integrais resolvidos. Universidade Nacional Experimental de Táchira.
- Leithold, L. (1992). O cálculo com geometria analítica. HARLA, S.A.
- Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Cálculo. México: Pearson Education.
- Saenz, J. (s.f.). Cálculo integral. Hipotenusa.


Ainda sem comentários