
Frações típicas, exemplos, exercícios resolvidos
As frações ou números fracionários são aqueles números que são representados indicando o quociente entre dois números inteiros para Y b, sempre e quando b é diferente de 0. Por exemplo, 1/3 é uma fração lida como “um terço”.
Para o número para É conhecido como numerador da fração e para b o que denominador da mesma. O denominador nos diz em quantas partes dividir o todo. Por sua vez, o numerador indica quantas partes desse todo foram tomadas.

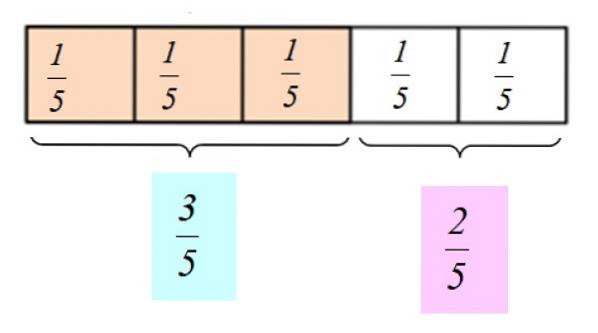
O todo é qualquer coisa que você queira dividir ou dividir, por exemplo uma pizza ou a barra de chocolate mostrada na figura 1. A barra é feita de tal forma que é muito fácil dividi-la em 5 partes iguais, onde cada parte é equivalente a 1/5 da barra completa.
Na fração ou número fracionário 1/5, o numerador é 1 e o denominador é 5. A fração é lida como "um quinto".
Suponha que comemos 3 pedaços de chocolate. Diríamos que já comemos 3/5 partes do bar e que sobraram 2/5 partes para partilhar com um amigo. Também podemos dizer que comemos "três quintos do chocolate" e demos "dois quintos" ao nosso amigo.
A representação gráfica desses números fracionários é a seguinte:
Índice do artigo
- 1 Tipos de frações
- 1.1 frações adequadas
- 1.2 Frações impróprias
- 1.3 Frações aparentes
- 1.4 Frações equivalentes
- 1.5 Frações irredutíveis
- 1.6 Números mistos
- 2 Exemplos de frações
- 2.1 Compra de alimentos
- 2.2 Receitas culinárias
- 2.3 Comprimentos e diâmetros
- 2.4 Intervalos de tempo
- 3 exercícios com frações
- 3.1 - Exercício 1
- 3.2 - Exercício 2
- 3.3 - Exercício 3
- 3.4 - Exercício 4
- 4 referências
Tipos de frações
Frações adequadas
Uma fração é apropriada quando o numerador é menor que o denominador e, portanto, seu valor é menor que 1. As frações na seção anterior, no exemplo do chocolate, são frações próprias..
Outros exemplos de frações adequadas são: ½; 8/10; 3/4 e mais.

Frações impróprias
O numerador das frações impróprias é maior que o numerador. Por exemplo, 4/3, 8/5, 21/10 pertencem a esta categoria.
Frações aparentes
Essas frações representam um número inteiro. Entre eles estão 4/2, 10/5 e 27/3, pois se olharmos de perto, o resultado da divisão do numerador pelo denominador dessas frações dá um número inteiro.
Assim: 4/2 = 2, 10/5 = 2 e 27/3 = 9.
Frações equivalentes
Duas frações n / me p / q são equivalentes quando a divisão do numerador pelo denominador resulta na mesma quantidade. Dessa forma, as frações equivalentes representam a mesma parte do todo..
Como exemplo temos as frações: 15/2 e 30/4. Ao dividir 15 por 2 você obtém 7,5, mas também é o mesmo se você dividir 30 por 4.
Para descobrir se duas frações n / me p / q são equivalentes, a seguinte igualdade é verificada:
n * q = m.p
Frações irredutíveis
Quando o numerador e o denominador são divididos pelo mesmo número e desde que o resultado seja um inteiro, obtém-se uma fração equivalente ao original, mas com números menores.
Este processo continua enquanto o numerador e o denominador tiverem exatamente o mesmo divisor. Quando não é possível continuar dividindo, o fração irredutível da fração original.
A vantagem de trabalhar com a fração irredutível é que se obtém uma fração equivalente, mas com números menores. Por isso, ao trabalhar com frações, certifique-se de reduzi-las sempre que possível, para facilitar os cálculos..
Suponha que a fração 12/20, sendo numerador e denominador pares, ambos podem ser divididos por 2:
20/12 = 10/06
E mais uma vez:
6/10 = 3/5
A fração 3/5 é equivalente a 12/20, mas mais simples.
Números mistos
Uma fração imprópria também admite representação como um número misto, assim chamado porque tem uma parte inteira e outra fracionária, sendo a parte fracionária uma fração própria..
Vejamos um exemplo rápido com a fração 15/2 que sabemos ser igual a 7,5.
Podemos expressar 15/2 como um número misto, como este:
15/2 = 7 + 0,5
Mas 0,5 = ½. Portanto, 15/2 = 7 ½ onde se lê "sete e meio".
Exemplos de frações
Os números fracionários são necessários porque tanto os naturais quanto os inteiros são insuficientes quando queremos dividir coisas como a barra de chocolate.
E é por isso que existe uma variedade infinita de padrões de medição e objetos cujas especificações incluem números fracionários, sem mencionar o número de situações cotidianas em que eles são necessários..
Compra de comida
Em países onde o sistema métrico é usado, é comum usar o quilo para se referir ao peso de muitos alimentos. Nem sempre queremos comprar quantidades inteiras, mas um pouco mais ou um pouco menos.
É por isso que pedimos:
- ½ kg de peixe
- ¾ kg de tomate
- ¼ quilo de cebola
- 1 ½ kg de pêssegos (1 quilo e meio).
E ao usar os padrões de medição anglo-saxões, a mesma coisa acontece: precisamos de 2 libras e meia ou 1/4 de libra de algo.
Todos esses números são fracionários e, como vimos, correspondem a dois tipos diferentes de frações: próprias e impróprias..
Receitas de cozinha
As receitas culinárias geralmente usam números fracionários para indicar a quantidade de certos ingredientes. Por exemplo:
- ½ xícara de farinha
- ¾ kg de açúcar para preparar um bolo.
Comprimentos e diâmetros
As dimensões dos móveis, peças têxteis e todo tipo de utensílios domésticos são medidas em frações de metro ou polegada, seja pelo sistema métrico ou pelo sistema decimal anglo-saxão de medidas..
Mesmo em países onde prevalece o sistema métrico, os tubos comerciais de cobre, aço e outros encanamentos geralmente vêm com diâmetros especificados em polegadas. Também outro hardware, como parafusos e porcas.
Como uma polegada equivale a 2,54 cm, essas peças, que têm diâmetros menores, costumam ser expressas em frações de uma polegada..
As medidas muito comuns para tubos domésticos são:
- ½ polegada
- ¼ polegada
- 3/8 e 5/8 polegadas.
Intervalos de tempo
Os números fracionários são usados diariamente para expressar intervalos de tempo como ¼, ½ e ¾ de uma hora, ou mesmo um pouco mais: 1 hora e ¼ e assim por diante.

Exercícios com frações
- Exercício 1
Hoje, Juanito trouxe para a escola um bolo de aniversário e quer distribuí-lo a todos os amigos, mas quer dar ao professor um pedaço três vezes maior que o das crianças.
Levando em consideração que são 24 crianças + a professora, a quem você quer dar o equivalente a três pedaços, em quantos pedaços você deve cortar o bolo??
Solução
Se Juanito quisesse apenas distribuir o bolo entre seus amigos, cada um teria 1/24.
Mas, como ele quer dar uma parte para a professora e que a peça é três vezes maior, ele teria que distribuir o bolo entre 24 alunos + 3 peças para a professora. Ou seja, cada criança corresponde a 1/27 peças e a professora a 3/27 peças.
Além disso, se reduzirmos a fração 3/27 obtemos que o professor pegará 1/9 do bolo.
- Exercício 2
Uma empresa com um chefe e três funcionários tem uma receita de € 6.000 por mês. Quanto dinheiro cada pessoa tem se o chefe quiser ficar com metade do que ganhou?
Solução
Se o patrão quiser ganhar metade, terá de ficar com 6.000/2, o que dá 3.000 €. Dos outros 3.000 euros restantes é o que os três funcionários terão de distribuir. Assim, cada funcionário ganhará 3000/3, resultando em € 1000.
- Exercício 3
Encontre a fração irredutível de:
a) 18/12 eb) 11/04
Solução para
No primeiro caso, notamos que tanto o numerador quanto o denominador são pares e divisíveis por 2. Eles também são divisíveis por 3, já que 12 e 18 são múltiplos desse número..
Portanto, podemos simplificar a fração dividindo o numerador e o denominador por 2 ou por 3, a ordem é indiferente.
Começando pela divisão por 2:
12/18 = 6/9
Agora, notamos que tanto o numerador quanto o denominador dessa fração equivalente são múltiplos de 3, portanto, dividindo ambos por este número:
6/9 = 2/3
E como 2 e 3 são números primos, eles não têm mais nenhum outro divisor comum, exceto 1. Chegamos à fração irredutível.
O maior divisor comum GCF do numerador e denominador também poderia ter sido calculado. Para 12 e 18:
GCF (12,18) = 6.
E então o numerador e o denominador são divididos por este número, o que é equivalente a fazer isso em estágios.
Solução b
Aqui observamos que 11 é um número primo e seus divisores são 1 e 11. Por sua vez, 4 admite 4, 2 e 1 como divisores. Com exceção de 1, esses números não têm um divisor comum e, portanto, a fração 4/11 é irredutível.
- Exercício 4
Indique qual é a maior fração de cada par:
a) ¾ e 5/4
b) 3/7 e 4/9
Solução para
Quando duas frações positivas têm o mesmo denominador, a maior é aquela que tem o maior numerador. Portanto, 5/4 é maior, pois 5> 3.
Solução b
Se as frações n / m e p / q tiverem denominadores diferentes e ambos forem positivos, o critério de comparação é o seguinte:
Se n.q> m. p, então n / m> p / q
Outra opção é encontrar a expressão decimal de cada fração e comparar.
De acordo com o primeiro critério: n = 3, m = 7, p = 4, q = 9. Portanto: n.q = 3 * 4 = 12 e m.p = 7 * 4 = 28.
Como 12< 28, ocurre que 3/7 < 4/9.
Ou expressamos cada fração como um decimal, obtendo o seguinte:
3/7 = 0,428571428… .
4/9 = 0,444444444 ... .
As reticências indicam que o número de casas decimais é infinito. Mas isso é o suficiente para verificar que, de fato, 4/9> 3/7.
Referências
- Baldor, A. 1986. Arithmetic. Edições e distribuições do Codex.
- Carena, M. 2019. Manual of Mathematics. Universidade Nacional do Litoral.
- Figuera, J. 2000. Mathematics 8. Ediciones Co-Bo.
- Jiménez, R. 2008. Algebra. Prentice Hall.
- A página da matemática. O que é uma fração? Recuperado de: themathpage.com.


Ainda sem comentários