Fórmula de frequência absoluta, cálculo, distribuição, exemplo

O Frequência absoluta É definido como o número de vezes que o mesmo dado se repete dentro do conjunto de observações de uma variável numérica. A soma de todas as frequências absolutas é equivalente a totalizar os dados.

Quando você tem muitos valores de uma variável estatística, é conveniente organizá-los adequadamente para extrair informações sobre seu comportamento. Tal informação é dada pelas medidas de tendência central e pelas medidas de dispersão..

Nos cálculos dessas medidas, os dados são representados pela frequência com que aparecem em todas as observações..

O exemplo a seguir mostra como a frequência absoluta de cada dado é reveladora. Durante a primeira quinzena de maio, estes foram os tamanhos de vestidos de coquetel mais vendidos em uma conhecida loja de roupas femininas:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Quantos vestidos são vendidos em um determinado tamanho, por exemplo, tamanho 10? Os proprietários estão interessados ​​em saber como fazer o pedido.

A ordenação dos dados facilita a contagem, há exatamente 30 observações no total, que ordenadas do menor tamanho ao maior são as seguintes:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

E agora é evidente que o tamanho 10 se repete 6 vezes, portanto sua frequência absoluta é igual a 6. O mesmo procedimento é realizado para descobrir a frequência absoluta dos tamanhos restantes..

Índice do artigo

• 1 Fórmulas
  • 1.1 Outras frequências
• 2 Como obter a frequência absoluta?
  • 2.1 Tabulação
  • 2.2 Tabela de frequência estendida
• 3 Distribuição de frequência
  • 3.1 Distribuição de frequência para dados agrupados
• 4 exemplo
• 5 Exercício resolvido
  • 5.1 Solução
• 6 referências

Fórmulas

A frequência absoluta, denotada como f_eu, é igual ao número de vezes que um certo valor X_eu está dentro do grupo de observações.

Supondo que o total de observações seja de N valores, a soma de todas as frequências absolutas deve ser igual a este número:

∑f_eu = f₁ + F_dois + F₃ +... f_n = N

Outras frequências

Se cada valor de f_eu dividido pelo número total de dados N, temos o frequência relativa F_r do valor X_eu:

F_r = f_eu / N

As frequências relativas são valores entre 0 e 1, porque N é sempre maior que qualquer f_eu, mas a soma deve ser igual a 1.

Multiplicando cada valor de f por 100_r você tem a frequência relativa percentual, cuja soma é 100%:

Frequência relativa percentual = (f_eu / N) x 100%

Também é importante Frequência acumulativa F_eu até uma determinada observação, esta é a soma de todas as frequências absolutas até e incluindo a referida observação:

F_eu = f₁ + F_dois + F₃ +... f_eu

Se a frequência acumulada for dividida pelo número total de dados N, temos o frequência relativa cumulativa, que multiplicado por 100 dá o porcentagem de frequência relativa cumulativa.

Como obter a frequência absoluta?

Para encontrar a frequência absoluta de um determinado valor que pertence a um conjunto de dados, todos eles são organizados do menor ao maior e o número de vezes que o valor aparece é contado.

No exemplo dos tamanhos dos vestidos, a frequência absoluta do tamanho 4 é de 3 vestidos, ou seja, f₁ = 3. Para o tamanho 6, 4 vestidos foram vendidos: f_dois = 4. No tamanho 8 4 vestidos também foram vendidos, f₃ = 4 e assim por diante.

Tabulação

Os resultados totais podem ser representados em uma tabela que mostra as frequências absolutas de cada um:

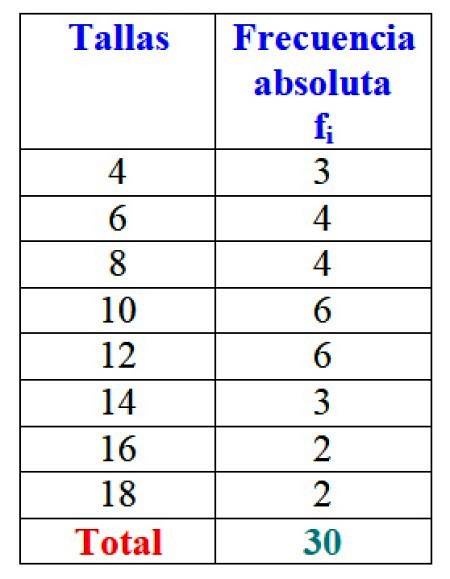
Obviamente, é vantajoso organizar as informações e poder acessá-las de relance, em vez de trabalhar com dados individuais.

Importante: observe que ao adicionar todos os valores da coluna f_eu  você sempre obtém o número total de dados. Caso contrário, você deve verificar a contabilidade, pois há um erro.

Tabela de frequência estendida

A tabela acima pode ser estendida adicionando os outros tipos de frequência em colunas sucessivas à direita:

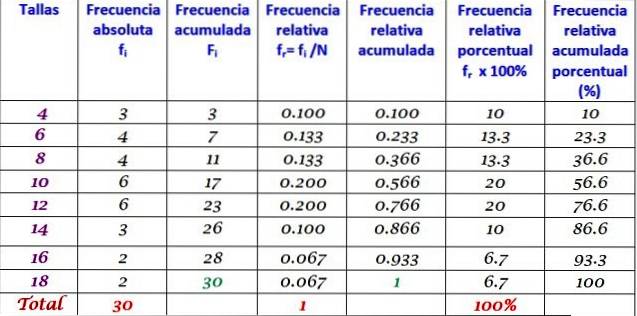
Distribuição de frequência

A distribuição de frequência é o resultado da organização dos dados em termos de suas frequências. Ao trabalhar com muitos dados, é conveniente agrupá-los em categorias, intervalos ou classes, cada um com suas respectivas frequências: absoluto, relativo, acumulado e percentual..

O objetivo de fazê-los é acessar mais facilmente as informações contidas nos dados, bem como interpretá-los adequadamente, o que não é possível quando estão apresentados desordenadamente..

No exemplo dos tamanhos, os dados não são agrupados porque não são muitos tamanhos e podem ser facilmente manipulados e contabilizados. Variáveis ​​qualitativas também podem ser trabalhadas desta forma, mas quando os dados são muito numerosos, é melhor trabalhar agrupando-os em classes.

Distribuição de frequência para dados agrupados

Para agrupar seus dados em classes de tamanhos iguais, considere o seguinte:

-Tamanho, largura ou amplitude da classe: é a diferença entre o valor mais alto da classe e o mais baixo.

O tamanho da classe é decidido dividindo a classificação R pelo número de classes a serem consideradas. O intervalo é a diferença entre o valor máximo dos dados e o menor, assim:

Tamanho da turma = Classificação / Número de turmas.

-Limite de aula: intervalo do limite inferior ao limite superior da classe.

-Marca de classe: é o ponto médio do intervalo, considerado representativo da classe. É calculado com a semi-soma do limite superior e do limite inferior da classe.

-Número de aulas: A fórmula de Sturges pode ser usada:

Número de classes = 1 + 3.322 log N

Onde N é o número de classes. Como geralmente é um número decimal, é arredondado para o próximo inteiro.

Exemplo

Uma máquina em uma grande fábrica está fora de operação devido a falhas recorrentes. Os períodos consecutivos de inatividade em minutos, da referida máquina, são registrados a seguir, com um total de 100 dados:

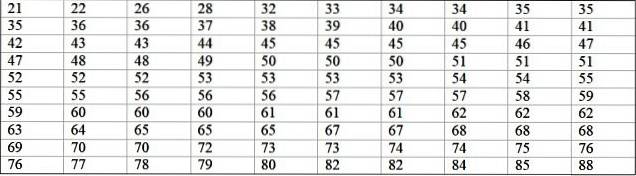
Primeiro, o número de classes é determinado:

Número de classes = 1 + 3.322 log N = 1 + 3,32 log 100 = 7,64 ≈ 8

Tamanho da classe = Faixa / Número de classes = (88-21) / 8 = 8.375

Também é um número decimal, então 9 é considerado o tamanho da classe.

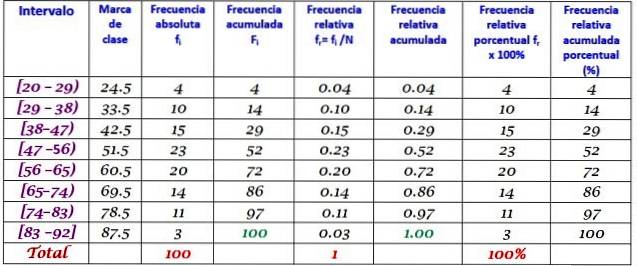
A nota da classe é a média entre os limites superior e inferior da classe, por exemplo, para a classe [20-29) há uma nota de:

Marca da classe = (29 + 20) / 2 = 24,5

Procedemos da mesma maneira para encontrar as marcas de classe dos intervalos restantes.

Exercício resolvido

40 jovens indicaram que o tempo em minutos que passaram na internet no último domingo foi o seguinte, ordenado em ordem crescente:

0; 12; vinte; 35; 35; 38; 40; Quatro cinco; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

É solicitada a construção da distribuição de frequência desses dados.

Solução

O intervalo R do conjunto de dados N = 40 é:

R = 220 - 0 = 220

Aplicar a fórmula de Sturges para determinar o número de classes produz o seguinte resultado:

Número de classes = 1 + 3.322 log N = 1 + 3,32 log 40 = 6,3

Por ser um decimal, o inteiro imediato é 7, portanto, os dados são agrupados em 7 classes. Cada classe tem uma largura de:

Tamanho da turma = Classificação / Número de turmas = 220/7 = 31,4

Um valor aproximado e arredondado é 35, portanto, uma largura de classe de 35 é escolhida.

As notas das aulas são calculadas pela média dos limites superior e inferior de cada intervalo, por exemplo, para o intervalo [0,35):

Marca da classe = (0 + 35) / 2 = 17,5

Proceda da mesma forma com as outras classes.

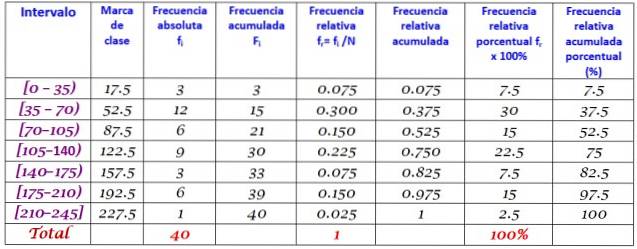
Por fim, as frequências são calculadas de acordo com o procedimento descrito acima, resultando na seguinte distribuição:

Referências

1. Berenson, M. 1985. Statistics for management and economics. Interamericana S.A.
2. Devore, J. 2012. Probability and Statistics for Engineering and Science. 8º. Edição. Cengage.
3. Levin, R. 1988. Statistics for Administrators. 2ª Edição. Prentice Hall.
4. Spiegel, M. 2009. Estatísticas. Schaum series. 4º Edição. Colina Mcgraw.
5. Walpole, R. 2007. Probabilidade e Estatística para Engenharia e Ciências. Pearson.