O Frequência acumulativa é a soma das frequências absolutas f, da mais baixa até aquela que corresponde a um determinado valor da variável. Por sua vez, a frequência absoluta é o número de vezes que uma observação aparece no conjunto de dados.
Obviamente, a variável de estudo deve ser classificável. E como a frequência acumulada é obtida somando as frequências absolutas, verifica-se que a frequência acumulada até os últimos dados, deve coincidir com o total deles. Caso contrário, há um erro nos cálculos.
Normalmente, a frequência cumulativa é denotada como Feu (ou às vezes neu), para distingui-lo da frequência absoluta feu e é importante adicionar uma coluna para ele na tabela com a qual os dados são organizados, conhecido como tabela de frequência.
Isso torna mais fácil, entre outras coisas, controlar quantos dados foram contados até uma determinada observação..
A Feu também é conhecido como frequência cumulativa absoluta. Se dividido pelo total de dados, temos o frequência cumulativa relativa, cuja soma final deve ser igual a 1.
Índice do artigo
A frequência cumulativa de um determinado valor da variável Xeu é a soma das frequências absolutas f de todos os valores menores ou iguais a ele:
Feu = f1 + Fdois + F3 +... feu
Ao somar todas as frequências absolutas, o número total de dados N é obtido, ou seja:
F1 + Fdois + F3 +… + Fn = N
A operação anterior é escrita de forma resumida por meio do símbolo de soma:
∑ Feu = N
As seguintes frequências também podem ser acumuladas:
-Frequência relativa: é obtido dividindo a frequência absoluta feu entre o total de dados N:
Fr = feu / N
Se as frequências relativas desde a mais baixa até a correspondente a uma determinada observação forem adicionadas, temos o frequência relativa cumulativa. O último valor deve ser igual a 1.
-Frequência relativa cumulativa percentual: a frequência relativa acumulada é multiplicada por 100%.
F% = (feu / N) x 100%
Essas frequências são úteis para descrever o comportamento dos dados, por exemplo, ao encontrar as medidas de tendência central.
Para obter a frequência acumulada, é necessário ordenar os dados e organizá-los em uma tabela de frequência. O procedimento é ilustrado na seguinte situação prática:
-Em uma loja online que vende celulares, o histórico de vendas de uma determinada marca no mês de março apresentava os seguintes valores por dia:
1; dois; 1; 3; 0; 1; 0; dois; 4; dois; 1; 0; 3; 3; 0; 1; dois; 4; 1; dois; 3; dois; 3; 1; dois; 4; dois; 1; 5; 5; 3
A variável é o número de telefones vendidos por dia e é quantitativo. Os dados apresentados desta forma não são tão fáceis de interpretar, por exemplo, os donos da loja podem ter interesse em saber se existe alguma tendência, como dias da semana em que as vendas dessa marca são mais elevadas..
Informações como essa e outras podem ser obtidas apresentando os dados de maneira ordenada e especificando as frequências..
Para calcular a frequência cumulativa, os dados são primeiro ordenados:
0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; dois; dois; dois; dois; dois; dois; dois; dois; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5
Em seguida, uma tabela é construída com as seguintes informações:
-A primeira coluna à esquerda com o número de telefones vendidos, entre 0 e 5 e em ordem crescente.
-Segunda coluna: frequência absoluta, que é o número de dias em que 0 telefones, 1 telefone, 2 telefones e assim por diante foram vendidos.
-Terceira coluna: a frequência acumulada, consistindo na soma da frequência anterior mais a frequência dos dados a serem considerados.
Esta coluna começa com os primeiros dados na coluna de frequência absoluta, neste caso é 0. Para o próximo valor, adicione-o ao anterior. Continua assim até atingir o último dado da frequência acumulada, que deve coincidir com o dado total.
A tabela a seguir mostra a variável "quantidade de telefones vendidos por dia", sua frequência absoluta e o cálculo detalhado de sua frequência acumulada.
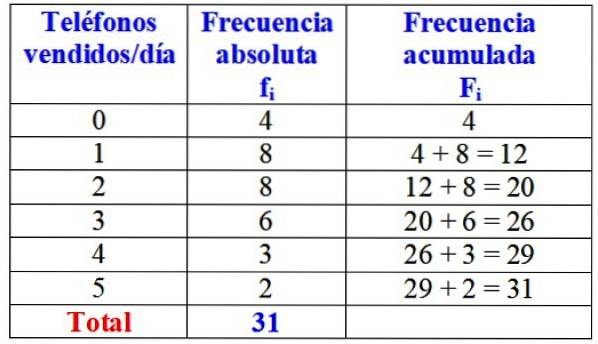
À primeira vista, pode-se afirmar que, da marca em questão, quase sempre são vendidos um ou dois telefones por dia, já que a maior frequência absoluta é de 8 dias, que corresponde a esses valores da variável. Só durante 4 dias do mês eles não venderam um único telefone.
Conforme observado, a tabela é mais fácil de examinar do que os dados individuais coletados originalmente.
Uma distribuição de frequência cumulativa é uma tabela que mostra as frequências absolutas, as frequências cumulativas, as frequências relativas cumulativas e as frequências percentuais cumulativas..
Embora haja a vantagem de organizar os dados em uma tabela como a anterior, se a quantidade de dados for muito grande, pode não ser suficiente organizá-los como mostrado acima, pois se houver muitas frequências, ainda fica difícil interpretar.
O problema pode ser resolvido com a construção de um distribuição de frequência por intervalos, um procedimento útil quando a variável assume um grande número de valores ou se é uma variável contínua.
Aqui, os valores são agrupados em intervalos de igual amplitude, chamados aula. As aulas são caracterizadas por ter:
-Limite de aula: são os valores extremos de cada intervalo, existem dois, o limite superior e o limite inferior. Em geral, o limite superior não pertence ao intervalo, mas ao próximo, enquanto o limite inferior pertence.
-Marca de classe: é o ponto médio de cada intervalo, e é considerado o valor representativo dele.
-Largura da classe: É calculado subtraindo o valor dos maiores e menores dados (intervalo) e dividindo pelo número de classes:
Largura da classe = intervalo / número de classes
A elaboração da distribuição de frequência é detalhada a seguir..
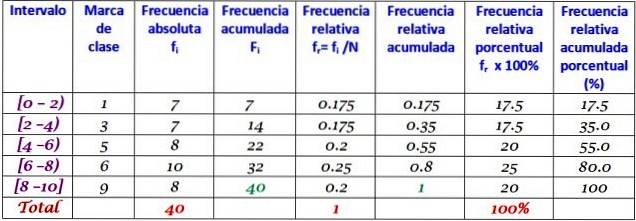
Este conjunto de dados corresponde a 40 notas de uma prova de matemática, em uma escala de 0 a 10:
0; 0; 0; 1; 1; 1; 1; dois; dois; dois; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.
Uma distribuição de frequência pode ser feita com um certo número de classes, por exemplo 5 classes. Deve-se ter em mente que ao usar muitas classes, os dados não são fáceis de interpretar e o sentido de realização do agrupamento se perde..
E se, ao contrário, eles são agrupados em muito poucos, então a informação se dilui e parte dela se perde. Tudo depende da quantidade de dados que você tem.
Neste exemplo, é uma boa ideia ter duas pontuações em cada intervalo, pois serão 10 pontuações e serão criadas 5 classes. O intervalo é a subtração entre a nota mais alta e a mais baixa, sendo a largura da classe:
Largura da classe = (10-0) / 5 = 2
Os intervalos são fechados à esquerda e abertos à direita (exceto o último), que é simbolizado por colchetes e parênteses respectivamente. Eles têm todos a mesma largura, mas não é obrigatório, embora seja na maioria das vezes.
Cada intervalo contém uma certa quantidade de elementos ou frequência absoluta, e na próxima coluna está a frequência acumulada, na qual a soma é transportada. A tabela também mostra a frequência relativa fr (frequência absoluta entre o número total de dados) e a frequência relativa percentual fr × 100%.
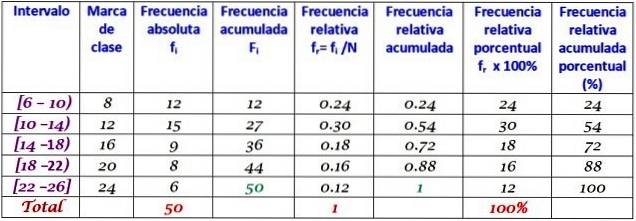
Uma empresa fez ligações diárias para seus clientes durante os primeiros dois meses do ano. Os dados são os seguintes:
6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 18, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 20, 13, 17, 14, 26, 7, 12, 24, 7
Agrupe em 5 classes e construa a tabela com a distribuição de frequência.
A largura da classe é:
(26-6) / 5 = 4
Tente descobrir antes de ver a resposta.
Ainda sem comentários