
Coeficiente de atrito estático, exemplo, exercício

O fricção estática é a força que surge entre duas superfícies quando uma superfície não desliza em relação à outra. É de grande importância, pois nos permite avançar ao caminhar, pois é a força presente entre o chão e a sola do calçado..
É também o atrito estático que surge entre o pavimento e os pneus do carro. Se essa força não estiver presente, então é impossível que o carro comece a se mover, como acontece em um carro que tenta dar a partida em uma superfície gelada: as rodas escorregam, mas o carro não se move.

O atrito estático depende da rugosidade das superfícies em contato e também do tipo de material de que são feitas. Por isso os pneus e calçados esportivos são feitos de borracha, para aumentar o atrito com o pavimento..
No modelo de atrito estático, as características dos materiais e o grau de rugosidade entre as superfícies são resumidos em um número denominado coeficiente de atrito estático, que é determinado experimentalmente.
Índice do artigo
- 1 Coeficiente de atrito estático
- 2 Exemplo: determinação do coeficiente de atrito estático
- 3 exercício
- 3.1 Solução
- 4 referências
Coeficiente de atrito estático

A figura acima mostra um livro que está parado sobre uma mesa com uma inclinação de 15,7º.
Se as superfícies do livro e da mesa fossem muito lisas e polidas, o livro não poderia ficar parado. Mas, como não são, aparece uma força tangente às superfícies em contato, chamada de força de fricção estática.
Se o ângulo de inclinação for grande o suficiente, então não há o suficiente força de atrito estático para equilibrar o livro e ele começaria a deslizar.
Nesse caso, também há atrito entre o livro e a mesa, mas isso seria um força de fricção dinâmica, também chamado atrito cinético.
Existe um limite entre o atrito estático e o atrito dinâmico, que ocorre no momento em que o atrito estático atinge seu valor máximo.
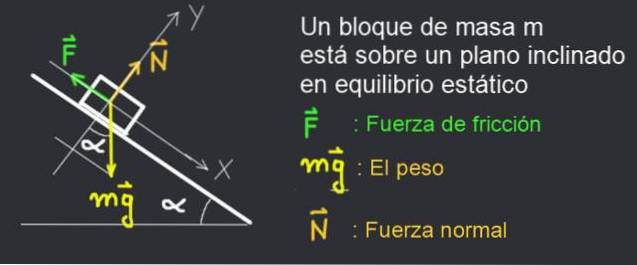
Consideremos na figura 2, o diagrama de força de um livro de massa m que é mantido em repouso em um plano de inclinação α.
O livro permanece em repouso porque a força de atrito estático F equilibra o sistema.
Se o ângulo de inclinação aumentar um pouco, então as superfícies em contato devem fornecer mais força de atrito, mas a quantidade de atrito estático que as superfícies em contato podem fornecer tem um limite máximo Fmax, quer dizer:
F ≤ Fmax.
A força máxima de atrito estático dependerá dos materiais e do grau de rugosidade das superfícies em contato, bem como da firmeza da garra.
O coeficiente de atrito estático μe é um número positivo que depende das características das superfícies em contato. Força normal N que o plano exerce sobre o bloco mostra o grau de aperto entre a superfície do bloco e o plano. É assim que eles determinam a força de atrito máxima que as superfícies fornecem quando não há deslizamento:
Fmax = µe N
Em resumo, a força de atrito estático segue o seguinte modelo:
F ≤ μe N
Exemplo: determinação do coeficiente de atrito estático
O coeficiente de atrito estático é um número adimensional determinado experimentalmente para cada par de superfícies.
Consideramos o bloco em repouso na figura 2. As seguintes forças atuam sobre ele:
- Força de fricção: F
- O peso do bloco de massa m: mg
- Força normal: N
Como o bloco está em repouso e não tem aceleração, de acordo com a segunda lei de Newton, a força resultante - uma soma vetorial - é zero:
F + N + mg = 0
Um sistema de coordenadas XY fixo é considerado com o eixo X ao longo do plano inclinado e o eixo Y perpendicular a ele, conforme mostrado na figura 2.
As forças devem ser separadas de acordo com seus componentes cartesianos, dando origem ao seguinte sistema de equações:
-Componente X: -F + mg Sen (α) = 0
-Componente Y: N - mg Cos (α) = 0
O valor da força de atrito estático é resolvido a partir da primeira equação:
F = mg Sen (α)
E a partir do segundo o valor da força normal:
N = mg Cos (α)
A força de atrito estático F obedece ao seguinte modelo:
F ≤ μe N
Substituindo os valores obtidos anteriormente na desigualdade temos:
mg Sen (α) ≤ μe mg Cos (α)
Considerando que para valores de α entre 0º e 90º, as funções seno e cosseno são ambas positivas, e que o quociente entre o seno e o cosseno é a tangente, temos:
Tan (α) ≤ μe
A igualdade vale para um determinado valor de α chamado ângulo crítico e que denotamos por α *, ou seja:
µe = Castanho (α *)
O ângulo crítico é determinado experimentalmente, aumentando gradativamente a inclinação até o ângulo reto em que o bloco começa a deslizar, que é o ângulo crítico α *.
No livro da figura 1, esse ângulo foi determinado experimentalmente resultando em 24 °. Então, o coeficiente de atrito estático é:
µe = Bronzeado (24º) = 0,45.
É um número positivo entre 0 e infinito. Se μe = 0 as superfícies são perfeitamente lisas. Se μe → ∞ as superfícies estão perfeitamente unidas ou soldadas.
Em geral, o valor do coeficiente de atrito está entre 0 e 10.
Exercício
Nas corridas de sprint ou dragster, são alcançadas acelerações de até 4g na largada, que são conseguidas justamente quando os pneus não escorregam em relação ao asfalto..
Isso ocorre porque o coeficiente de atrito estático é sempre maior do que o coeficiente de atrito dinâmico..
Assumindo que o peso total do veículo mais o motorista é de 600 kg e que as rodas traseiras suportam 80% do peso, determine a força de atrito estático durante a partida de 4g e o coeficiente de atrito estático entre os pneus e o pavimento..

Solução
De acordo com a segunda lei de Newton, a força resultante é igual à massa total do veículo vezes a aceleração que ele adquire.
Como o veículo está em equilíbrio vertical, o normal e o peso se anulam, deixando como resultante a força de atrito F que o pavimento exerce sobre a área de contato das rodas de tração, restando que:
F = m (4g) = 600 kg (4 x 9,8 m / sdois) = 23520 N = 2400 kg-f
Isso significa que a força de tração é de 2,4 toneladas.
A força de atrito que a roda exerce sobre o solo vai para trás, mas sua reação, que é a mesma e oposta, atua sobre o pneu e avança. Essa é a força que move o veículo.
Claro, toda essa força é produzida pelo motor que tenta empurrar o piso de volta através da roda, mas a roda e o piso são acoplados pela força de atrito.
Para determinar o coeficiente de atrito estático utilizamos o fato de que o F obtido é o atrito máximo possível, uma vez que estamos no limite da aceleração máxima, portanto:
F = μe N = μe (0,8 mg)
Foi levado em consideração o fato de as rodas motrizes traseiras suportarem 0,8 vezes o peso. Resolvendo o coeficiente de atrito, obtemos:
µe = F / (0,8 mg) = 23520 N / (0,8 x 600 kg x 9,8 m / s ^ 2) = 5.
Conclusão: μe = 5.
Referências
- Alonso M., Finn E. 1970. Física, volume I: Mecânica. Fundo Educacional Interamericano S.A.
- Bauer, W. 2011. Physics for Engineering and Sciences. Volume 1. Mc Graw Hill.
- Hewitt, P. 2012. Conceptual Physical Science. Quinta edição.
- Rex, A. 2011. Fundamentals of Physics. Pearson. 190-200.
- Jovem, Hugh. 2015. University Physics with Modern Physics. 14º Ed. Pearson.


Ainda sem comentários