O força centrífuga tende a empurrar os corpos girando em torno de uma curva. É considerado um força fictícia, pseudoforce ou força inercial, porque não é causado por interações entre objetos reais, mas é uma manifestação do inércia dos corpos. Inércia é a propriedade que faz com que os objetos queiram preservar seu estado de repouso ou de movimento retilíneo uniforme, se houver..
O termo "força centrífuga" foi cunhado pelo cientista Christian Huygens (1629-1695). Ele afirmou que o movimento curvilíneo dos planetas tenderia a afastá-los, a menos que o Sol exercesse alguma força para retê-los e ele calculou que essa força era proporcional ao quadrado da velocidade e inversamente proporcional ao raio da circunferência descrita..
Para quem viaja de carro, a força centrífuga não é nem um pouco fictícia. Passageiros em um carro que vira à direita se sentem empurrados para a esquerda, e vice-versa, quando o carro vira à esquerda, as pessoas experimentam uma força à direita, que parece querer afastá-los do centro da curva.
A magnitude da força centrífuga Fg é calculado usando a seguinte expressão:
-Fg é a magnitude da força centrífuga
-m é a massa do objeto
-v é a velocidade
-R é o raio do caminho curvo.
Força é um vetor, portanto, o tipo negrito é usado para distingui-lo de sua magnitude, que é um escalar.
Você deve sempre ter em mente que Fg aparece apenas quando o movimento é descrito usando um quadro de referência acelerado.
No exemplo descrito no início, o carro girando constitui uma referência acelerada, uma vez que requer o aceleração centrípeta, então eu posso me virar.
Índice do artigo
A escolha do sistema de referência é vital para a apreciação do movimento. Um referencial acelerado também é conhecido como referencial não inercial..
Nesse tipo de sistema, como um carro girando, aparecem forças fictícias como a centrífuga, cuja origem não é uma interação real entre objetos. Um passageiro não pode dizer o que o empurra para fora da curva, ele só pode afirmar que é esse o caso.
Por outro lado, em um sistema de referência inercial, as interações ocorrem entre objetos reais, como o corpo em movimento e a Terra, que dá origem ao peso, ou entre o corpo e a superfície sobre a qual se move, que originam o atrito e normal.
Um observador parado na beira da estrada e observando o carro fazer a curva é um bom exemplo de sistema de referência inercial. Para esse observador, o carro gira porque uma força direcionada para o centro da curva atua sobre ele, o que o força a não sair dele. É sobre o força centrípeta produzida pelo atrito entre os pneus e o pavimento.
Em um referencial inercial, a força centrífuga não aparece. Portanto, o primeiro passo para calculá-lo é escolher cuidadosamente o sistema de referência que será usado para descrever o movimento..
Por fim, deve-se notar que os sistemas de referência inercial não precisam necessariamente estar em repouso, como o observador que observa o veículo fazer a curva. Um referencial inercial, conhecido como quadro de referência do laboratório, também pode estar em movimento. Claro, com velocidade constante em relação a um inercial.
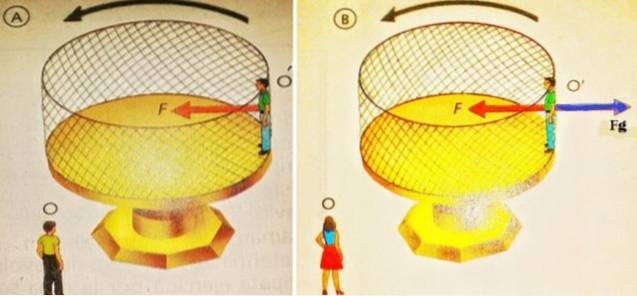
Na próxima figura à esquerda, um observador O está parado olhando para O ', que está na plataforma que gira na direção indicada. Para O, que é uma estrutura inercial, certamente O 'continua girando devido à força centrípeta Fc produzido pela parede da grade na parte de trás do O '.
Somente em referenciais inerciais é válido aplicar a segunda lei de Newton, que afirma que a força resultante é igual ao produto da massa pela aceleração. E ao fazer isso, com o diagrama de corpo livre mostrado, obtemos:
Fc = mac
Fc= mvdois / R
Da mesma forma, na figura à direita também há um diagrama de corpo livre que descreve o que o observador O 'vê. Do seu ponto de vista, ele está em repouso, portanto, as forças sobre ele se equilibram.
Essas forças são: o normal F, que a parede exerce sobre ela, em vermelho e direcionada para o centro e a força centrífuga Fg que empurra para fora e que não é originada por nenhuma interação, é uma força não inercial que aparece nos referenciais rotativos.
A força centrífuga sendo fictícia, é equilibrada por uma força real, o contato ou força normal que aponta para o centro. Portanto:
∑Fx = 0 → Fg - F = 0
Fg = F
Embora a força centrífuga seja considerada uma pseudo força, seus efeitos são bastante reais, como pode ser visto nos exemplos a seguir:
- Em qualquer jogo giratório em um parque de diversões, a força centrífuga está presente. Ela garante que "fugimos do centro" e oferece resistência constante se você tentar caminhar até o centro de um carrossel em movimento. No seguinte pêndulo você pode ver a força centrífuga:
- O efeito Coriolis surge da rotação da Terra, o que faz com que a Terra deixe de ser uma moldura inercial. Em seguida, aparece a força Coriolis, que é uma pseudo-força que desvia os objetos lateralmente, como as pessoas que tentam andar em uma plataforma giratória..
Um carro que gira com aceleração PARA à direita está um brinquedo de pelúcia pendurado no espelho retrovisor interno. Desenhe e compare os diagramas de corpo livre do brinquedo vistos em:
a) O quadro de referência inercial de um observador parado na estrada.
b) Um passageiro viajando no carro.
Um observador parado na estrada percebe que o brinquedo está se movendo rapidamente, com aceleração PARA para a direita.
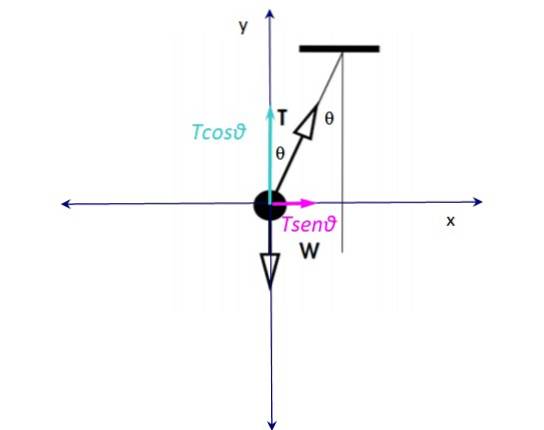
Existem duas forças agindo sobre o brinquedo: por um lado, a tensão no fio T e peso vertical para baixo C. O peso é equilibrado com o componente vertical de tensão Tcosθ, portanto:
W - Tcosθ = 0
O componente horizontal do estresse: T. senθ é a força desequilibrada responsável pela aceleração para a direita, portanto a força centrípeta é:
Fc= T. sinθ = mac
Para um passageiro no carro, o brinquedo está em equilíbrio e o diagrama é o seguinte:
Como no caso anterior, o peso e a componente vertical da tensão são compensados. Mas o componente horizontal é equilibrado pela força fictícia Fg = mA, de tal forma que:
-mA + Tsenθ = 0
Fg = mA
Uma moeda está na ponta de uma velha vitrola de vinil, cujo raio é de 15 cm e gira a uma velocidade de 33 rotações / minuto. Encontre o coeficiente de atrito estático mínimo necessário para que a moeda permaneça no lugar, usando o quadro de referência de solidariedade com a moeda.
Na figura está o diagrama de corpo livre de um observador movendo-se com a moeda. O normal N que a plataforma giratória exerce verticalmente para cima é equilibrada com o peso C, enquanto a força centrífuga Fg é compensado por atrito estático Ftoque.
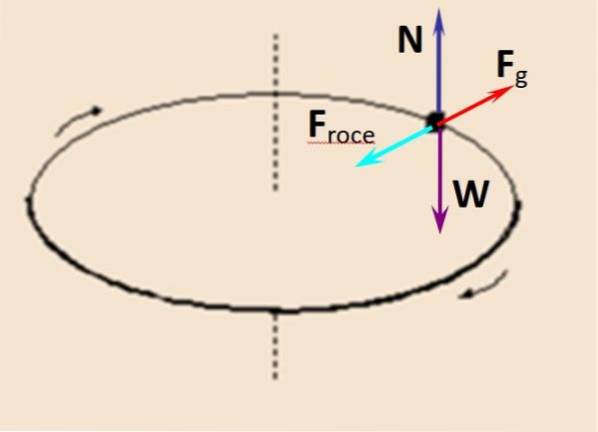
N - W = 0
Ftoque - Fg = 0
A magnitude da força centrífuga é mvdois/ R, como disse no início, então:
Ftoque = Fg = mvdois/ R
Por outro lado, a força de atrito estático é dada por:
Fesfregar = µs.N
Onde µs é o coeficiente de atrito estático, uma quantidade adimensional cujo valor depende de como as superfícies estão em contato. Substituir esta equação é:
µs.N = mvdois/ R → μs = mvdois/R.N
Resta determinar a magnitude do normal, que está relacionado ao peso de acordo com N = mg. Substituindo novamente:
µs = mvdois/R.mg → μs = vdois/ Rg
De volta ao comunicado, ele informa que a moeda gira a uma taxa de 33 rotações / minuto, que é a velocidade angular ou frequência angular ω, relacionado à velocidade linear v:
v = ω.R = 33 rev / min. 2π radianos / rev. 15 cm. (1 min / 60 s) = 51,8 cm / s
µs = vdois/Rg=(51,8 cm / s)dois/ (15 cm x 981 cm / sdois) = 0,18
Os resultados deste exercício teriam sido os mesmos se um referencial inercial tivesse sido selecionado. Nesse caso, a única força capaz de causar aceleração em direção ao centro é o atrito estático..
Como já dissemos, a força centrífuga é uma força fictícia, que não aparece nos referenciais inerciais, os únicos em que valem as leis de Newton. Neles, a força centrípeta é responsável por fornecer ao corpo a aceleração necessária em direção ao centro.
A força centrípeta não é uma força diferente das já conhecidas. Pelo contrário, são precisamente eles que desempenham o papel de forças centrípetas quando apropriado. Por exemplo, a gravidade que faz a Lua orbitar em torno da Terra, a tensão em uma corda pela qual uma pedra é girada, o atrito estático e a força eletrostática.
No entanto, como os referenciais acelerados são abundantes na prática, as forças fictícias têm efeitos muito reais. Por exemplo, aqui estão três aplicações importantes onde têm efeitos tangíveis:
Centrífugas são instrumentos amplamente utilizados em laboratório. A ideia é fazer com que uma mistura de substâncias gire em alta velocidade e aquelas com maior massa experimentem uma maior força centrífuga, conforme a equação descrita no início..
Assim, as partículas mais massivas tenderão a se afastar do eixo de rotação, separando-se das mais leves, que ficarão mais próximas do centro..
As máquinas de lavar automáticas têm diferentes ciclos de centrifugação. Neles as roupas são centrifugadas para eliminar a água restante. Quanto mais rotações do ciclo, menos úmidas estarão as roupas no final da lavagem.
Os carros são melhores nas curvas nas estradas, porque a pista se inclina ligeiramente em direção ao centro da curva, o que é conhecido como superelevação. Dessa forma, o carro não depende exclusivamente do atrito estático entre os pneus e a estrada para fazer a curva sem sair da curva..
Ainda sem comentários