
Força resultante como é calculado e exercícios resolvidos
O força resultante é a soma de todas as forças que atuam no mesmo corpo. Quando um corpo ou objeto é submetido à ação de várias forças simultaneamente, ocorre um efeito. As forças de atuação podem ser substituídas por uma única força que produz o mesmo efeito. Esta única força é a força resultante também conhecida como força resultante e é representada pelo símbolo FR .
O efeito que produz FR vai depender de seu tamanho, direção e sentido. Quantidades físicas que têm direção e sentido são quantidades vetoriais.
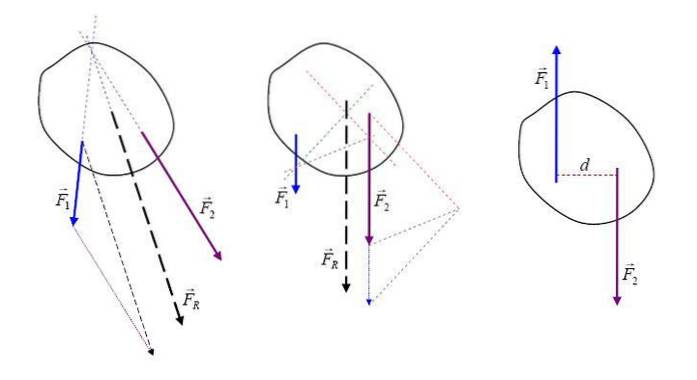
Sendo as forças agindo sobre as magnitudes de um vetor de corpo, a força resultante FR é uma soma vetorial de todas as forças e pode ser representada graficamente com uma seta que indica sua direção e direção.
Com a força resultante, o problema de um corpo afetado por várias forças é simplificado, reduzindo-o a uma única força atuando.
Índice do artigo
- 1 Fórmula
- 2 Como você calcula a força resultante?
- 2.1 resultante de forças paralelas
- 2.2 Forças não paralelas
- 3 exercícios resolvidos
- 4 referências
Fórmula
A representação matemática da força resultante é uma soma vetorial das forças.
FR= ∑F (1)
∑F = F1+ Fdois+ F3+... FN (dois)
FR= Força resultante
∑F = Soma das Forças
N= Número de Forças
A força resultante também pode ser representada pela equação da segunda lei de Newton.
FR= m.para (3)
m= massa corporal
a = aceleração corporal
Se a equação (1) for substituída na equação (3), as seguintes equações são obtidas:
∑F = m.para (4)
F1+ Fdois+ F3+... FN = m.para (5)
As expressões matemáticas (4) e (5) fornecem informações sobre o estado do corpo através da obtenção do vetor de aceleração para.
Como você calcula a força resultante?
A força resultante é obtida pela aplicação da Segunda Lei de Newton, que afirma o seguinte:
A força resultante atuando sobre um corpo é igual ao produto de sua massa e a aceleração que adquire. (Equação (3))
A aceleração do corpo terá a direção da rede de força aplicada. Se todas as forças que atuam sobre o corpo forem conhecidas, basta adicioná-las vetorialmente para obter a força resultante. Da mesma forma, se a força resultante for conhecida, bastaria dividi-la pela massa do corpo para obter sua aceleração..
Se a força resultante for zero, o corpo está em repouso ou em velocidade constante. Se uma única força atua no corpo, a força resultante é igual a essa força FR=F.
Quando várias forças atuam em um mesmo corpo, deve-se levar em consideração os componentes do vetor da força e se essas forças são paralelas ou não..
Por exemplo, se deslizarmos horizontalmente um livro colocado sobre uma mesa, as forças na direção horizontal são as únicas que proporcionam aceleração ao corpo. A força vertical líquida no livro é zero.
Se a força aplicada ao livro tem uma inclinação em relação ao plano horizontal da mesa, a força é escrita em função dos componentes vertical e horizontal.
Resultante forças paralelas
As forças paralelas que atuam em um corpo são aquelas forças que atuam na mesma direção. Eles podem ser de dois tipos de sentido igual ou oposto.
Quando as forças que atuam sobre um corpo têm a mesma direção e a mesma direção ou estão na direção oposta, a força resultante é obtida realizando a soma algébrica dos valores numéricos das forças.
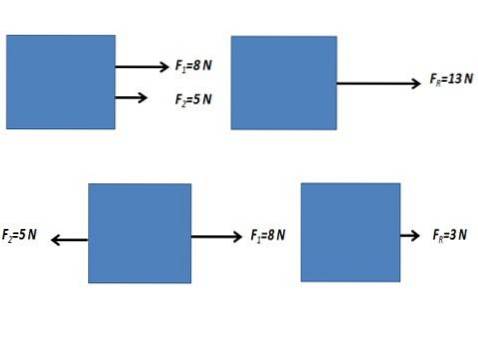
Forças não paralelas
Quando forças não paralelas são aplicadas a um corpo, a resultante das forças terá componentes retangulares e verticais. A expressão matemática para calcular a força resultante é:
FRdois= (∑ Fx)dois+(∑ FY)dois (6)
tão θx= ∑ FY / ∑ Fx (7)
∑ Fx e ∑ Fx= Soma algébrica dos componentes x e Y de forças aplicadas
θx= ângulo formado pela força resultante FR com eixo x
Observe que a força resultante da expressão (6) não está destacada em negrito e é porque expressa apenas o valor numérico. A direção é determinada pelo ângulo θx.
A expressão (6) é válida para forças atuando no mesmo plano. Quando as forças atuam no espaço, o componente é levado em consideração z de força ao trabalhar com componentes retangulares.
Exercícios resolvidos
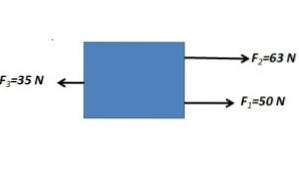
As forças paralelas na mesma direção são adicionadas e subtraídas com a força paralela na direção oposta
FR= 63 N + 50 N - 35 N = 78N
A força resultante tem uma magnitude de 78N com direção horizontal.
2. Calcule a força resultante de um corpo sob a influência de duas forças F1 Y Fdois. A força F1 ele tem uma magnitude de 70N e está sendo aplicado horizontalmente. A força Fdois tem uma magnitude de 40N e está sendo aplicado em um ângulo de 30 ° em relação ao plano horizontal.
Para resolver este exercício, um diagrama de corpo livre é desenhado com os eixos coordenados x e Y
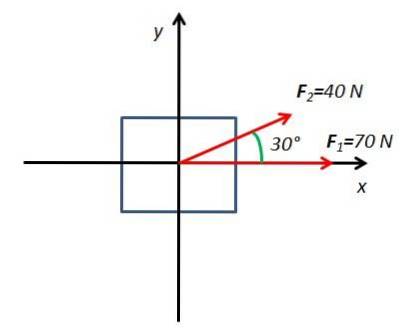
Todos os componentes são determinados x e Y das forças que atuam no corpo. A força F1 tem apenas um componente horizontal no eixo x. A força Fdois tem dois componentes F2x e F2 e que são obtidos a partir das funções seno e cosseno do ângulo de 30 °.
F1x = F1=70N
F2x = Fdois cos 30 ° = 40 N. cos 30 ° = 34,64N
F1a = 0
F2 e= Fdois sem 30 ° = 40 sem 30 ° = 20N
∑ Fx =70N + 34,64N = 104,64N
∑ FY=20N + 0 = 20N
Uma vez que as forças resultantes no eixo foram determinadas x e Y procedemos para obter o valor numérico da força resultante.
FRdois= (∑ Fx)dois+(∑ FY)dois
A força resultante é a raiz quadrada da soma dos componentes quadrados das forças
FR= √ (104.64N)dois+(20N)dois
FR= 106,53N
O ângulo formado pela força resultante FR é obtido a partir da seguinte expressão:
θx= então-1(∑ FY / ∑ Fx)
θx= tão-1(20N / 104,64N) = 10,82 °
A força resultante FR tem uma magnitude de 106,53N e tem uma direção determinada pelo ângulo de 10,82 ° que forma com a horizontal.
Referências
- Dola, G, Duffy, M e Percival, A. Física. Espanha: Heinemann, 2003.
- Avison, J H. O mundo da Física. Índia: Thomas Nelson and Sons, 1989.
- Pinsent, M. Processos Físicos. Reino Unido: Nelson Thomas, 2002.
- Yadav, S K. Engenharia Mecânica. Delhi: Discovery Publishing House, 2006.
- Serway, R A e Jewett, J W. Física para cientistas e engenheiros. Califórnia, EUA: Brooks / Cole, 2010.



Ainda sem comentários